Complete Solutions to Mathematics of chapter ONLINE QUESTION PAPER of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | ONLINE QUESTION PAPER |
| TS EAMCET | Mathematics |
| Number Of Questions | 80 |
| Academic Year | 2023-24 |
If `f: [1, oo) rarr [5, oo)` is given by `f(x) = 3x + (2)/(x)`, then `f^(-1) (x) =`
View SolutionThe domation of `f(x) = log [(25)^(3-x^(2)) - (0.4)^(x + 9)]` is
View SolutionLet `n in N` which one of the following is true?
View SolutionIf `A = [(1,2,2),(2,1,2),(2,2,1)], " then " A^(-1)=`
View SolutionIf x, y are any two non-zero real numbers, `a_(ij) =xi + yj, A = (a_(ij))_(m xxn)` and P, Q are two `n xx n` matrices such that A = xP + yQ, then
View SolutionIf the system `[(2,8),(3,7)][(a),(b)]= k [(a),(b)]` has non-trivial, solution then the positive value of k and a solution of the system for that value of k are
View SolutionThe modulus-amplitude form of `((1-i)^(3) (2-i))/((2+i) (1 +i))` is
View SolutionIf `z_(1) =2 -3i and z_(2) = -1 + i`, then the locus of a point P represented by `z = x +iy` in the argand plane satisfying the equation arg `((z-z_(1))/(z-z_(2))) = (pi)/(2)` is
View Solution`((1 + "cos"(pi)/(8) -i "sin"(pi)/(8))/(1 + "cos"(pi)/(8) + i "sin" (pi)/(8)))^(12)=`
View SolutionIf the complex number a is such that `|a|=1 and` arg(a) =`theta`, then the roots of the equation `((1 + iz)/(1-iz))^(4) = a` are z=
View SolutionIf `x^(2) + 2px - 2p + 8 gt 0` for all real values of x, then the set of all possible values of p is
View SolutionIf the roots of the equation `(p-3) x^(2) + 2(p -3) x + 2p-5 =0` are real number distinct for `alpha lt p lt beta and (beta - alpha)` is maximum, then the extreme value of the quadratic expression `-(alpha + beta) x^(2) + alpha beta x+ (alpha -beta)` is
View SolutionIf the equation `x^(3) -7x^(2) + 14x -8=0` is trasformed to `y^(3) + py - (20)/(27) =0` when its roots are diminshed by k, then p=
View SolutionIf one root of the equation `x^(3) - 9x^(2) + 26x -24=0` is twice the other. Then, the sum of the cubes of those two roots is
View SolutionThere are 10 points in a plane of which no three points are collinear except 4. Then, the number of distinct triangles that can be formed by joining these points such that atlest one of the vertices of every triangle formed is formed the given 4 collinear points is
View SolutionThe number of ways of arranging 8 boys and 8 girls in a row so that boys and girsl sit alternately is
View SolutionIf the coefficients of `(2alpha + 4)th and (alpha-2)th` terms in the expansion `(1 + x)^(2019)` are equal, then `alpha=`
View SolutionIf n is a positive interger, then the coefficient of `x^(6)` in the expansion of `(1-2x + 3x^(2) -4x^(3) + …)^(-n)` is
View Solution`(d)/(dx) ((x +5)/((x + 1)^(2) (x+2)))=`
View SolutionIf the period of the function f(x) `= sin 5x cos 3x` is `alpha`, then `cos alpha=`
View SolutionIf `"cos"(pi)/(15) "cos"(2pi)/(15) "cos"(4pi)/(15)`
`"cos"(5pi)/(15) "cos"(7pi)/(15) "cos"(30pi)/(15) =x, " then " (1)/(8x) =`
View SolutionIf `A + B + C = 2S`, then `sin (S-A) + sin (S-B) - sin C=`
View SolutionWhen a is irrational, the number of solutions satisfying the equation `1 + sin^(2) ax = cos x` is
View Solution`tan^(-1) ((1)/(2 sqrt2)) + sin^(-1) ((1)/(sqrt3)) = cos^(-1) x, " then " x=`
View Solution`"Tanh"^(-1)((1)/(3))+"coth"^(-1)(3)=`
View SolutionIF the angles of a triangle are in the ratio `1:2:3`, the corresponding sides are in the ratio
View SolutionTwo ships leave a port from a point at the same time. One goes with a velocity of 3kh/h along North-East making an angle of `45^(@)` with East direction and the other travels wth a velocity of 4km/h along South-East making an angle of `15^(@)` with East direction. Then, the distance between the ships at the end of two hours is
View SolutionIn `DeltaABC, r_(1) + r_(2) + r_(3)=`
View SolutionIn a quadrilateral PQRS, A divides SR in the ratio `1 : 3` and B is the mid-point of PR. If `3SR-QR-3PS-PQ =kAB`, then k=
View SolutionIt is given that a,b,c are vectors of lengths 6,8,10 respectively. If a is perpendicular to `(b+c), b` is perpendicular`(c+a)`, and c is perpendicular to `(a+b)`, then the length of the vector of |`a+b+c`| is
View SolutionIf the direction cosines of two lines are given by `l + 3m +5n=0 and 5lm - 2mn + 6ln = 0`, then the angle between the lines is
View SolutionIf a, b, c,d are 4 vector such that a.b =0, `|a xx c| = |a||c|, |a xx d| = |a||d|, " then " [bcd]=`
View SolutionIf a, b, c are three non-coplanar vectors and d is any unit vector, then
`|(a.d)(bxx c) + (b.d) (c xx a) + (c .d) (a xx b)|=`
View SolutionIf the line r = a + lb is parallel to the plane `r = c + ld + "me"`, then
View SolutionThe mean derviation about the mean for the following data, is
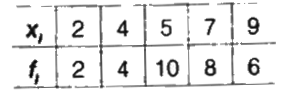
View SolutionIf the coefficients of variation of two distributions are 40 and 20 and their variances are 144 and 64 respectively, then the mean of their arithmetic means is
View SolutionA number n is chosen at random from the natural numbers 2 to 1001. The probability that n is a number that leaves remainder 1 when divided by 7, is
View SolutionIf A and B are two independent events such that `P(B) =(2)/(7) and P(A uuB^(C )) = 0.8, " then " p(A uuB)`=
View SolutionIn a certain recruitment test with multiple choice questions, there are four options to answer each question, out of which only one is correct. An intelligent student knows 90% correct answers while a weak student known only 20% correct answers. If an intelligent student gets the correct answer for a question, then the probability that he was guessing it, is
View SolutionIf the mean and variance of a Binomial variable X are `(5)/(2) and (5)/(4)` respectively, then `P(X gt 1)=`
View SolutionIf a random variable X follows a poisson distribution such that `P(X=1) =3P (X=2)`, then `P(x=3)=`
View SolutionLet `Q(x_(1), y_(1))` be a variable point and `R(1,0)` be a point on the circle `x^(2) + y^(2) =1 and P` be the mid -point of QR. Then, the locus of the point P is
View SolutionThe point P(3,2) undergoes the following transformations successively
(i) Reflection about the line y=x
(ii) Translation to a distance of 3 units in the positive direction of X-axis
(iii) Rotation through an angle `(pi)/(4)` about the origin in the anti-clockwise direction
Then , the final position of that point is
View SolutionThe equation of the straight line which is perpendicular to the line `5x-2y =7` and passing through the point of intersection of the lines `2x + 3y-1 =0 and 3x + 4y -6 = 0` is
View SolutionThe angle between the line joining the points (1,-2), (3,2) and the line `x + 2y -7 =0` is
View SolutionThe vectices of a triangle are `A(1,7), B(-5, -1) and C(-1, 2)`. Then, the equation of a bisector of the `angleABC` is
View SolutionShow that two pairs of lines `3x^(2)+8xy-3y^(2)=0 and 3x^(2)+8xy-3y^(2)+2x-4y-1=0` forms a square.
View SolutionThe equation of pair of lines passing through origin and forming an equilateral triangle with the line `3x + 4y -5 = 0` is
View SolutionFrom a point A(1,0) on the circle `x^(2) + y^(2) - 2x + 2y + 1 =0`, a chord AB is drawn and it is extended to a point P such that AP = 3AB. The equation of the locus of P is
View SolutionShow that the tangent at `(-1, 2)` of the
circle `x^(2) + y^(2) - 4x -8y + 7 = 0`
touches
the circle `x^(2) + y^(2) + 4x + 6y = 0` and also
find its point of contact.
View SolutionIf `C_(1) and C_(2)` are the centres of similitude with respect to the circles `x^(2) + y^(2) -14x + 6y + 33 =0 and x^(2) + y^(2) + 30x -2y + 1=0`, then the equation of the circle with `C_(1) C_(2)` as diameter is
View SolutionIf tangents are drawn to the circle `x^(2) + y^(2) = 12` at the points of intersection with the circle `x^(2) + y^(2) -5x + 3y -2 =0`, then the ordinate of the point of intersection of these tangents is
View SolutionFrom a point P on the line `4x-5y=6` two tangents are drawn to the circle `x^(2) + y^(2) -6x -4y + 4 = 0`. If the angle between these tangents is `tan^(-1) ((24)/(7))`, then P =
View SolutionIf `(-1,-1)` is the focus and `x + y + 3=0` is the directrix of a parabola, then its vertex is
View SolutionIf a normal chord of a parabola `y^(2) = 4ax` subtends a right angle at the origin, then the slope of that normal chord is
View SolutionIf origin is the centre, X-axis is the major axis and `sqrt((2)/(5))` is the eccentricity of an ellips which passes through `(-3,1)` then the equation of that ellipse is
View SolutionThe slope of a common tangent to the ellipse `(x^(2))/(49) + (y^(2))/(4) =1` and the circle `x^(2) + y^(2) = 16` is
View SolutionThe distance between the tangents drawn to the hyperbola `3x^(2) -y^(2) = 3`, that are parallel to the line `y= 2x + 4` is
View SolutionIf the distance between two points A and B is d, and the lengths of the projections of AB on the coordinate planes are `d_(1), d_(2), d_(3)`, then
View SolutionL is a line passing through the point A(1, 0, -3) and parallel to a line having direction rations 0, 1, -2, P is a point on the line L which is at a minimum distance from the plane `2x + 3y + 5z =1`. Then, the equation of the plane through P and perpendicular to AP is
View SolutionLet `pi_(1)` be the plane passing through the points (0,1,2), (1,0,-2), (-2, 1,0) and `p_(2)` be the plane passing through the point (1, 2,3) and perpendicular to the planes `x + y + z =1 and 2x-3y + z =5`. If `theta` is the acute angle between the planes `pi_(1) and pi_(2)` then `cos theta=`
View Solution`underset(x rarr 0)(lim) (cos 4x - 4 cos 2x + 3)/(x^(4)) =`
View SolutionIf `alpha = underset(x rarr 0)Lt (x.2^(x) -x)/(1 - cos x) and beta = underset(x rarr 0)(Lt) (x.2^(x) -x)/(sqrt(1 + x^(2)) -sqrt(1-x^(2)))`, then
View SolutionIf `f(x) = (2)/(4 + 3|x|), x in R`, then f(0) =
View SolutionIf f is a real function such that f(4) = 4 and `f'(4) = 16, " then " underset(x rarr 4)(lim) (sqrt(f(x))-2)/(sqrtx-2)=`
View SolutionIf `y= (sin^(-1) 2x)^(2) + (cos^(-1) 2x)^(2)`, then `(1-4x^(2))y_(2) - 4xy_(1)=`
View SolutionLet `f(x) = x^(3) + 2x^(2) -x` be a real valued function. Then, the value of Langrange's constant C in (-1, 2)is
View Solution`int Tan^(-1)((2x)/(1-x^(2)))dx=`
View SolutionThe angle between the curves `y= sin 2x and y = cos 2x` is
View SolutionThe ratio between the length of substangent at any point other than origin on the parabola `y^(2) = 16ax` and the abscissa of that point is
View Solution` int(dx)/(sqrt((x-1)(x-2)))`
View SolutionIf `int (x^(4) + 1)/(x^(6) + 1) dx = A tan^(-1) x + B tan^(-1) x^(3) + c`, then (A,B) =
View SolutionIf `int x(1 + x) log (1 + x^(2)) dx = F(x)`
`log (1 + x^(2))-(2)/(3) tan^(-1)x - (2x^(3))/(9) - (x^(2))/(2) + (2x)/(3) + c`, then F(x) =
View SolutionIf `I_(n) = int cos^(n) x dx`, then `6I_(6) -5I_(4) =`
View SolutionIf `f(x) = (|log x|)/(x^(2)), " then " int_(1//e)^(e ) f(x) = dx=`
View SolutionThe area enclosed by the curves `y= 8x -x^(2) and 8x -4y +11 =0` is
View SolutionIf `I = int_(0)^(pi//2) (dx)/(5 + 3 sin x) = lamda tan^(-1) ((1)/(2))`, then `lamda=`
View SolutionThe general solution of the differential equation `((1)/(x^(2)) + x) (dy)/(dx) + 3y = 1` is
View SolutionA family of curves whose equation is general solution of a differential equation having order 1 and degree 3, is
(g, a, c are arbitrary constants)
View SolutionThe general solution of the differential equation `(dy)/(dx) = (1)/(x + y +1)` is
(k, c are arbitrary constant)
View Solution
Mathematics questions and complete solutions for chapter ONLINE QUESTION PAPER of TS EAMCET PREVIOUS YEAR PAPERS of Class 12