Complete Solutions to Mathematics of chapter QUESTION PAPER 2019 of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | QUESTION PAPER 2019 |
| TS EAMCET | Mathematics |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
The domain of the function
`f(x)=sin^(-1)[log_(4)(x/4)]+sqrt(17x-x^(2)-16)` is
View SolutionIf `f:[1, oo)rarr[2, oo)` is given by `f(x)=x+(1)/(x)` then `f^(-1)(x)=`
View SolutionIf the greatest divisor `30*5^(2n)+4*2^(3n)` is `p, AA n in N` and that of `2^(2n+1)-6n-2` is `q, AA n in N`, then `p+q=`
View SolutionIf `A=[(0,5),(0,0)]` and `f(x)=x+x^(2)+...+x^(2018)`, then `f(A)+I=`
View SolutionIf a , b, c are real numbers such that `a-b=1, b-c=3`, then the number of matrices of the form `A[(1,1,1),(a,b,c),(a^(2),b^(2),c^(2))]` such that `|A|=-12`, is
View SolutionFor what values of 'a' , the system of equations `x+y+z=1, 2x+3y+2z=2, ax+ay+2az=4` will have a unique solution ?
View SolutionIf `z_(n)=(1+isqrt(2))^(n), n in Z`, then `1/9 R e (z_(4) bar(z)_(5))=`
View SolutionIf `z=x+iy`, then the centre of the circle `|(z-3)/(z-2i)|=2`, is
View SolutionIf z is a complex number such that `|z+4|ge3,` then the smallest value of `|z+3|` is
View SolutionThe real part of z that satisfies `iz^(4)+1=0` is
View SolutionIf `x` is real, then the interval in which no value of the expression `(2(x^(2)+2x-11))/(2x-5)` lies, is
View SolutionThe set of all real values of `x` satisfying the inequalities `x^(2)-4x+3 gt0` and `x^(2)-2x-8 le 0`, is
View SolutionIf the roots `alpha, beta , gamma` of the equation `x^(3)-6x^(2)+px+10=0`are in arithmetic progression, then `alpha^(3)+beta^(3)+gamma^(3)=`
View Solution`alpha, beta , gamma` are the roots of the cubic equation `x^(3)+p_(1)x^(2)+p_(2)x+p_(3)=0`. If `S_(r)=alpha^(r)+beta^(r)+gamma^(r), S_(1)=10, S_(2)=38` and `S_(3)= - 1840`, then `p_(3)=`
View SolutionThe number of 4 letter permutations formed with English alphabet such that the number of distinct vowels is equal to the number of distinct consonants, when repetition is allowed, is
View SolutionA student is asked to answer 10 out of 13 questions is an examination such that he must answer atleast four questions from the first five questions. The number of choices available to him is
View SolutionIf the `17^(th)` and the `18^(th)` terms in the expansion of `(2+a)^(50)` are equal, then the coefficient of `x^(35)` in the expansion of `(a+x)^(-2)` is
View SolutionIf the `k^(th)` term in the expansion of `(3/2 x^(2)- (1)/(3x))^(6)` is independent of `x`, then the numerically greatest term in the expansion of `(3/2 x^(2)- (1)/(3x))^(k)` when `x=2/3`, is
View SolutionIf `(27x^(2)+32x+16)/((3x+2)^(2)(1-x))=(A)/(3x+2)+(B)/((3x+2)^(2))+(C)/(1-x)`, then `AB+BC+CA=`
View SolutionIf the angles of depression of the top and bottom of a short building from the top of a tall building are `30^(@)` and `60^(@)` respectively, then the ratio of the heights of short and tall buildings is
View SolutionFind the value of `cos 18^(@)`
View SolutionIf `A+B+C=pi`, then `sinA-sinB+sinC=`
View SolutionFor `n in Z`, the general solution of the trigonometric equation `sin x-sqrt(3) cos x +4 sin 2x-4sqrt(3)cos 2x+sin 3x-sqrt(3)cos 3x=0` is
View SolutionFor `a gt 0`, if `f(x)=ax+b` is an onto function from `[-1,1]` to `[0,2]` then `cot[tan^(-1). 1/7 +tan^(-1). 1/8+tan^(-1) . 1/5]=`
View SolutionThe solution of the equation `2cos h 2x+10 sin h 2x=5` is
View SolutionIn a triangle `ABC`, if `a^(2)-b^(2)-c^(2)=bc(lambda^(2)-2lambda-1)`, then
View SolutionIf a and b respectively represent the lengths of a side and a diagonal of a regular pentagon that is inscribed in a circle, then `b/a=`
View SolutionIn a right angled triangle, if the difference between the two acute angles is `60^(@)`, then the ratio of the lengths of the hypotenuse and the perpendicular drawn to the hypotenuse from its opposite vertex is
View SolutionIf the position vectors of the points A, B, C, D given by `hat(i)+2hat(j)+3hat(k), 2hat(i)-hat(j)+2hat(k), 1/4(7hat(i)+15hat(j)+15hat(k))` and `1/3 [ 7 hat(i)+2hat(j)+(5+3a)hat(k)]` respectively are such that `|AC|=|BD|`, then `16(3a-1)^(2)=`
View SolutionIf the points `2a+3b-c, a-2b+3c, 3a+lambda b-2c` and `a-6b+6c` are coplanar, then the direction cosines of the vector `lambda hat(i)-2lambda hat(j)+hat(k)` are
View SolutionIf `L_(1)` is a line through the point `5hat(i)+8hat(j)+11hat(k)` and parallel to the vector `2hat(i)+3hat(j)+4hat(k)` and `L_(2)` is a line through the point `4 hat(i)+6hat(j)+8hat(k)` and parallel to the intersection of `L_(1)` and `L_(2)` is
View Solution`a=4hat(i)+3hat(j)` and b are two vectors in `XOY` plane and a is perpendicular to b. A vector c lying in the same plane and having projections 1 and 2 respectively a and b is
View SolutionIf `OA=6hat(i)+3hat(j)-4hat(k), OB=2hat(j)+hat(k), OC=5hat(i)-hat(j)+2hat(k)` are the coterminous edges of a parallelopiped, then the height of the parallelopiped drawn from the vertex A is
View SolutionThe shortest distance between the lines
`r=(-2hat(i)+hat(j)-hat(k))+r(3hat(i)+3hat(j)-hat(k))` and
`r=(hat(i)-hat(j)+2hat(k))+k(-1hat(i)+2hat(j)+4hat(k))` is
View SolutionThe mean deviation from the median of the data 16, 22, 3, 14, 5, 10, 8, 6, 11, 4 is
View SolutionThe variance of the following frequency distribution is
`{:("Class Interval",0-4,4-8,8-12,12-16,16-20),("Frequency",2,4,6,3,1):}`
View SolutionThe two events `E_(1), E_(2)` are such that
`P(E_(1)uuE_(2))=5/8, P (bar(E)_(1))=3/4, P(E_(2))=1/2`, then `E_(1)` and `E_(2)` are
View SolutionIf a die is rolled twice and the sum of the numbers appearing on them is observed to be 6, then the probability that the number 1 appears atleast once on them is
View SolutionAn examination is attempted by 5000 graduates, 2000 post-graduates and 1000 doctorate holders, The probabilities that a graduate, a post graduate and a doctorate holder will pass the examination are `2/3, 3/4, 4/4` respectively. If one of the examine passed the examination, then the probability that he is a post-graduate is
View SolutionThe pobability distribution of a discrete random variable X is given below. If
`E(X^(2))=Sigma x^(2)P(X=x)`, then `6E(X^(2))-Var(X)=`
`{:(X=x,-1,0,1,2,),(P(X=x),1/3,1/6,1/6,1/3,):}`
View SolutionIf X is a Poision variable representing number of successes in 50 trials such that `2P(X=1)=5P(X=5)+2P(X=3)`, then the probability of getting succes in one trial is
View SolutionLet `{:(l rarr 0),(lim):}(1+5t)^(1/t)=K` and X be the random variable representing number of successes in 100 independent trials. If the probability of success in each trial is 0.05, then the probability of getting at least one success is
View SolutionIf the origin is shifted to a point (h, k) by translation of axes in order to make the equation `x^(2)+5xy+2y^(2)+5x+6y+7=0` free from first order terms, then
View SolutionSuppose a line makes an angle of `120^(@)` with the positive direction of X-axis. If the length of the perpendicular from origin to that line is 4, then the equation of the line is
View SolutionTwo straight lines are drawn through the points (0, 2) such that the length of the perpendiculars from the point (4, 4) to these lines are each equal to 2 units. The equation of the line joining the feet of these perpendiculars is
View SolutionTwo points `A(-a, 0)` and `B(a, 0)` are given. If C is a variable point lying on one side of the line AB such that `angleCAB- angleCBA=alpha`, where `alpha` is a positive constant, then locus of the point C is
View SolutionIf the angle between the pair of lines `x^(2)+2sqrt(2)xy+ky^(2)=0, k gt 0` is `45^(@)`, then the area ( in square units) of the triangle formed by the pair of bisectors of angles between the given lines and the line `x+2y+1=0` is
View SolutionIf d is the distance between the point of intersection of the lines
`x^(2)+4xy+ky^(2)-4x-10y+3=0` and the origin and p is the product of the perpendicular distances from the origin to these lines, then `d^(2)-20p^(2)=`
View SolutionA line meets coordinate axes in A and B. A circle is circumscribed about the triangle OAB . If m and n are distances of tangent to circle at origin from the point A and B respectively then diameter of the circle is
View SolutionThe centre of the circle passing through the point (0, 1) and touching the curve `y=x^(2)` at (2, 4) is
View SolutionIf the number of common tangents to the pair of circles `x^(2)+y^(2)-2x+4y-4=0` and `x^(2)+y^(2)+4x-4y+alpha=0` is 4, then the least integral value of `alpha` is
View SolutionFind the equation of the circle which
touches the circle `x^(2) + y^(2) - 2x - 4y - 20 = 0`
externally at `(5, 5)` with radius 5.
View SolutionThe equation of a circle with the circle `x^(2)+y^(2)-6x+12y+15=0` and having area that is twice the area of the given circle is
View SolutionIf the locus of a point which divides a chord with slope 2 of the parabola `y^(2)=4x`, internally in the ratio `1:3` is a parabola, then its vertex is
View SolutionIf the normal at one end of the latusrectum of the parabola `y^(2)=16x` meets the X-axis at the point P, then the length of the chord passing through P and perpendicular to the normal is
View SolutionAssertion (A) If the tangent and normal to the ellipse `9x^(2)+16y^(2)=144` at the point `P(pi/3)` on it meet the major axis in Q and R respectively, then `QR=(57)/(8)`.
Reason (R) If the tangent and normal to the ellipse `(x^(2))/(a^(2))+(y^(2))/(b^(2))=` at the point `P(theta)` on it meet the major axis in Q and R respectively, then `QR=|(a^(2)sin^(2)theta-b^(2)cos^(2)theta)/(a cos theta)|`
The correct answer is
View SolutionIf `x+y+n=0, n gt 0` is a normal to the ellipse `x^(3)+3y^(2)=3` and `x^(2)+5y^(2)=5`, then the point of intersection of these two lines satisfy the equation
View SolutionThe product of lengths of the perpendiculars from the point of the hyperbola `x^(2)-y^(2)=8` to its asymptotes is
View SolutionIf a triangle ABC with two vertices A(5, 4, 6) and B(1, -1, 3) has its centroid at `((10)/(3), 2, (11)/(3))` then the third vertex C is
View SolutionLet ABC be a triangle with `A(alpha, 5, beta), B(-2,1,6) ` and `C(1, 0, -3)` as its vertices. If the median through B is equally inclined to the coordinate axes, then `alpha+beta=`
View SolutionThe equation of the plane in cartesian form, which is at a distance of `(6)/(sqrt(29))` from the origin and its normal vector drawn from the origin being `2 hat(i)-3hat(j)+4hat(k)`, is
View Solution`{:(" lim"),(x rarr 0):}((sinh 2x)/(2x))^(1/x^(2))=`
View SolutionIf the function `f:R rarr R` defined by
`{:{(a((1-cos2x)/(x))",","for " x lt 0 ),(" b, " ,"for "x=0),((sqrt(x))/(sqrt(4+sqrt(x))-2)",","for "x gt 0):}`
is continuous at `x=0`, then `a+b=0`
View SolutionIf `f(x)=cos h ^(-1)((1-x)/(1+x))` is well defined, then `f'(x)=`
View SolutionMatch the items of List-I with those of List-II
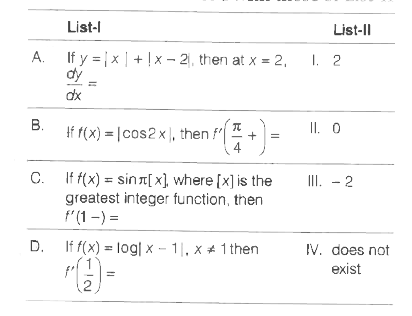
The correct matching is
View SolutionIf `(dy)/(dx)=4` and `(d^(2)x)/(dy^(2))=-3` at a point P on the curve `y=f(x)`, then `((d^(2)x)/(dy^(2)))_(p)=`
View SolutionThe approximate value of `tan^(-1)(0.999)` ( upto 4 decimal places) is
View SolutionIf the normal to the curve `y=f(x)` at (1, 2) make an angle `(3pi)/(4)` with positive X-axis, then
`f'(1)=`
View SolutionThe number of real roots of the equation `e^(x-1)+x-2=0` is
View SolutionLet `f:D rarr R, D sube R , c in D ` and r be a non zero real number. Consider the following statements :
I. c is an extreme point of `f rArr c ` is an extreme point of `rf`
II. c is an extreme point of `f rArrc ` is an extreme point of `r+f`
Which of the following is correct ?
View Solution`int (dx)/((1+x)sqrt(8+7x-x^(2)))=`
View Solution`int (x^(3)+2x)/(x^(4)+4)dx=`
View SolutionEvaluate: `int(x+1)/(x\ (1+x\ e^x)^2)\ dx`
View Solution`int sec^(5)x dx =`
View Solution`int_(pi/4)^(pi/2) cot^(9)x dx=`
View SolutionLet `f(x)` be an even function with period 2 and `f(x)` be integrable on every interval . If `g(x)= int_(0)^(x) f(t) dt`, then `g(x+2)=`
View SolutionLet `[x]` be greatest integer function. Then, `int_(-1)^(1) [ x +2[x+2[x]]]dx=`
View SolutionIf k and `l` respectively are the order and degree of the differential equation whose general solution represents the family of circles of constant radius, then `k^(2)+ l^(2)=`
View SolutionThe solution of the differential equation `(dy)/(dx)=1-cos(y-x)cot(y-x)` is
View SolutionThe general solution of the differential equation `( y sin x + y)(dy)/(dx)-cos^(2)x=0`
View SolutionIf : R - `{(3)/(7) rarr R - {(3)/(7)}` is given by f(x) = `(3x + 5)/(7x - 3)`, then the statement which is not true, is
View SolutionIf `f: AvecBa n dg: BvecC` are onto functions show that `gof` is an onto function.
View SolutionThe sum of first n terms of the series `(3)/(5) + (21)/(25) + (117)/(125) + ….` is
View SolutionThe sum of the values of x so that the matrix
`({:(2,2,1),(1,3,1),(1,2,2):})` -x `({:(1,0,0),(0,1,0),(0,0,1):})` is singular, is
View SolutionIf `A=[(cos alpha, -sin alpha, 0),(sin alpha, cos alpha,0),(0,0,1)]` then `A^(-1)` is
View SolutionIf abc `ne` 0 and the system of equations
x + 7 ay + 2az = 0, x + 6 by + 2 bz = 0,
x + 5cy + 2cz = 0 has a non-zerotrivial solution, then a,b,c are in
View Solution`z_(1) , z_(2)` are two complex numbers with `|z_(1) - z_(2)| lt ` k. If the complex number z satisfies the condition `|z_(1) - z_(2)| + |z - z_(2)| `= k , then z lies on
View SolutionIn the complex plane C, the set
`{z in C : arg((z - 1)/(z + 1)) = (pi)/(4)}` represents
View SolutionIf ` z_(1) = a + ib " and " z_(2) + c id ` are complex numbers such that ` |z_(1)| = |z_(2)| = 1 ` and ` Re (z_(1)bar (z)_(2)) = 0 `,
then the pair of complex numbers ` w_(1) = a + ic " and " w_(2) = b id ` satisfies :
View SolutionIf ` ( 1 + x ) ^(n) = a_(0) + a _(1) x + a_(2) x^(2) + ………. + a_(n)x^(n) ` , then show that
(i) ` a_(0) - a_(2) + a_(4) - a_(6) + ……… = 2^(n//2) cos . (npi)/4 `
(ii) ` a _(1) a_(3) + a_(5) - a_(7) + …….. = 2^(n//2) sin . (npi)/4 `
View SolutionFor x `gt` 2, then equation
`sqrt(x + 2) - sqrt(x - 2) = sqrt(4x - 2)` has
View SolutionIf x `in` R, then the range of `(x)/(x^(2)-5x + 9)` is
View SolutionIf `alpha, beta, gamma ` are the roots of the equation `x^(3) - ax^(2) + bx -c = `0 , then `sum alpha^(2) (beta + gamma)= `
View SolutionThe equation whose roots are reciprocals of the roots of `6x^(6) - 25x^(5) + 31x^(4) - 31x^(2)` + 25x - 6 = 0 ` is
View SolutionThe number of five digit numbers that are divisible by 6 which can be formed by choosing digits from {0, 1, 2, 3, 4, 5}, when repetition is allowed, is
View SolutionA person invites 8 guests to a dinner and places 5 of them at one table and the remaining 3 at another, both the tables being round. The number of ways in which the guests can be arranged is
View SolutionIf `15^(k)` divides 47! But `15^(k + 1)` does not divide it, then k =
View SolutionIf `(1 + x + x^(2))^(n) = c_(0) + c_(1) x + c_(2) x^(2) + …. , ` then the value of `c_(0)c_(1) - c_(1)c_(2) + c_(2)c_(3) - ……` is
View SolutionIf x is so small that `x^(2)` and higher powers of x can be neglected, then the approximate value of `(1 + (3)/(4)x )^((1)/(2)) (1 - (2x)/(3))^(-2)` is
View SolutionIf `(x^(4))/((x - a)(x - b)(x - c)) = P(x) + (A)/(x - a) + (B)/(x - b) + (C )/(x - c),` then P(0) + A(a - b)(a - c) =
View Solution
Mathematics questions and complete solutions for chapter QUESTION PAPER 2019 of TS EAMCET PREVIOUS YEAR PAPERS of Class 12