Complete Solutions to MATHEMATICS of chapter TS EAMCET 2019 (4 MAY SHIFT 2) of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | TS EAMCET 2019 (4 MAY SHIFT 2) |
| TS EAMCET | MATHEMATICS |
| Number Of Questions | 80 |
| Academic Year | 2023-24 |
Find the domain of the real function `f(x)=(1)/(sqrt([x]^(2)-[x]-2)`.
View SolutionLet `f : R to R` and `g: R to R` be the functions
defined by `f(x) = (x)/(1 + x^2) ` ,
` x in R , g(x) = (x^2) /(1 + x^2) , x in R`
Then, the correct statement (s) among the following is/are :
(a) both f.g are one-one
(b) both f.g are onto
(c) both f.g are not one-one as well as not onto
(d)f and g are onto but not one-one
View SolutionIf ` alpha in R, n in N " and " n + 2 (n - 1)+ 3 (n-2) + …… +(n-1)2 + n.1 = alpha n ( n + 1) (n + 2) , " then " alpha = `
View SolutionIf the function `f : [a, b] to [ - (sqrt3)/(4) ,1/2]` defined by
`f(x) = |{:(1, 1, 1), (1, 1 + sin x , 1), (1+cos x, 1 , 1):}|`
is one - one and onto , then
View SolutionThe rank of the matrix
`[{:(3, 5, - 1, 4 ), (2, 1, 3, -2), (8, 11 , 1 , 6), (-7, -14, 6, -14):}]`
View SolutionA value of e for which the following system of equations has a non-trivial solution is
`(4 sin theta) x-3y +z =0,-(6 cos 2theta) y + z = 0, 3x - 12y + 4z = 0`
View SolutionIf `z = sqrt(2) sqrt(1 + sqrt(3i)) ` represents a point P in the argand plane and P lies in the third quadrant, then the polar form of z is
View SolutionIf z = x + iy represents a point P in the argand plane, then the area of the region represented by the inequality 2 <|z-(1+i)|<3 is
View SolutionIf P is a complex number whose modulus is one, then the equation ` ( (1 + iz)/(1 - iz) )^4` = P has
View Solution`sum_(r =1)^(16) ( sin [(2r pi)/(17)] + icos [(2rpi)/(17)] )` =
View SolutionIf the maximum value of `2x - 7-ax^2` cannot exceed 20, then the minimum value of a is
View SolutionA student while solving a quadratic equation in x, he copied its constant term incorrectly and got its roots as 5 and 9. Another student copied the constant term and coefficient of `x^2` of the same equation correctly as 12 and 4 respectively. Ifs,p and `Delta` denote respectively the sum of the roots, the product of the roots and the discriminate of the correct equation,
then `(Delta)/(3p + s) = `
View SolutionThe product of the real roots of the equation `(x + 1)^4 + (x + 3)^4 = 8 ` is
View SolutionThe sum of all the real numbers satisfying the equation `x^2 + | x - 3 | = 4` is
View SolutionConsider the following statement :
(i) Numberof one-one functions from set A to set B, where O(A) = m and O(B) =` n(m lt=n)` is given by `""^nP_m`
(ii) Number of ways is which 'n' people can be arranged at a circular table is `( (n-1)!)/(2)`
(iii) Number of ways of selecting atleast one thing out of the given a distinct things is `2^n - 1`
(iv) Number of ways in which distinguishable objects can be distributed into k distinguishable bins is `""^nC_(k-1) `
Then which one of the following is true?
View SolutionThe number of ways is which 3 identical balls can be distributed into 7 distinct bins is
View SolutionLet `(1+ x + x^2)^n = a_0 + a_1x + a_2x^2 + …….+a_(2n)x^(2n)`
Then match the items of List - I with those of List-II

The correct match is
View SolutionFor `x = 5/7` , If `t_k` is the first negative term in the expansion of `(1+x)^(7//5) `, then ` t_1, + t_2, + …..t_k = `
View SolutionThe cofficient of `x^6` in the tower series expansion of `(x^4 - 12x^2 + 7)/((x^2 + 1)^3)` is
View SolutionShow that `(1+ cos. (pi)/(8))(1+cos. (3pi)/(8))(1+ cos. (5pi)/(8))(1+ cos .(7pi)/(8))=(1)/(8)`
View SolutionIf A and B are acute angles satisfying
` 3 cos^2 A + 2 cos^2 B = 4 " and " (3 sin A)/(sin B) = (2cos B)/(Cos A)` ,
then ` A + 2B = `
View SolutionIf A + B + C = `pi/3` then
`sin ( (pi-6A)/(6) ) + sin ( (pi -6B)/(6) )+sin C = `
View SolutionIf ` sqrt(2) sin^2 x + (3sqrt(2) + 1) sin x + 3 gt 0` and ` x^2 - 7x + 10 lt 0 ` , then x lies in the interval
View SolutionIf `cos^(-1) x + cos^(-1) y + cos^(-1) z = 3pi ` , then
View SolutionIf `sin h^(-1) ( sqrt8) + sin h^(-1) ( sqrt24) = alpha` , then sin h ` = alpha`
View SolutionIn a triangle ABC . If
`cos Acos B + sin A sin B sin C = 1` , then `sin A + sin B+ sin C = `
View SolutionIn a `Delta ABC` , if the medians AD and BE are such that AD = 4 , `angle DAB = pi/6 " and " angle ABE = pi/3` then the area of `Delta ABC` (in square units) is
View SolutionIn a `Delta ABC , " if " r_1 = 2r_2 = 3r_3 , ` then a : b = `
View SolutionIf a and b are respectively the internal and external bisectors of the angles between the vetors ` -hati + 2 hatj - 2 hatk " and " 3 hati + 4 hatj " and " |a| = 2/3 sqrt6, | b | = 2/3 sqrt3` , then one of the values of a - b is
View SolutionIf the angle between the vectors
` 2 alpha^2hati + 4 alpha hatj + hatk" and " 7 hati - 2 hatj + alpha hatk ` is obtuse then
View SolutionLet L be the line parallel to the vectors `sqrt(2) hati - 5 hatj + 3 hatk ` and passing through the point a given by `hati + 2 hatj - 3 hatk` . If the distance between A and a point P on the line L is 18 units , then the position vector of such a point P is
View SolutionLet `a = p (hati + hatj + hatk ).b = hati + hatj - 2 hatk " and " c= 2 hati - hatj + 2 hatk ` be three vecotrs . If the values of [a b c] is not more than15 and not lees than -5, then the p lies in the interval
View SolutionLet `a = hati + 2 hatj - hatk " and" b = hati + hatj+ hatk`. If p is a unit vecotr such that [abp] is maximum then p =
View SolutionIf ` a = 2 hati - 3 hatj + hatk, b = hati - hatj + 2 hatk " and " c = 2hati + hatj + hatk` are three vecotrs , then ` |(a xx b) xx c | = `
View SolutionThe mean deviation about the median of the following distributions is
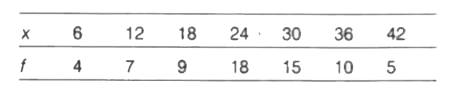
View SolutionFor a group of 100 observations, the arithmetic mean and standard deviation are 8 and `sqrt(10.5) ` respectively. The mean and standard deviation of 50 items selected from these 100 observations are 10 and 2 respectively. Then the standard deviation of the remaining 50 observation is
View SolutionIf a number is selected from the first 30 natural numbers, then the probability that the number selected is divisible by 4 or 7, is
View SolutionIf 80% of flights depart on time, 70% of flights arrive on time and 65% of flights depart on time and arrive on time, then the probability that a flight that has just departed on time will arrive on time is
View SolutionA computer program has two modules X and Y and errors in them occur independently. X has an error with probability 0.1 and Y has an error with probability 0.3. If an error in X alone cause the program to crash with probability 0.5, an error in Y alone causes the program to crash with probability 0.7 and an error in both X and Y cause the program to crash with probability 0.8, then the probability that the program is crashed is
View SolutionTwo dice are rolled. If a random variable X denotes the sum of the numbers on them and `mu` denotes the mean of X, then
`mu + P (X lt 5) + P ( X gt 9) + P ( x = 7) = `
View SolutionA boy rolled a die once. If an even number appear on then the number of chocolates the boy gets is equal to two more then the number appeared. If an odd number appear on that die. Then the number of chocolates he gets is equal to three more than the number'appeared. If a random variable X represents the number of chocolates the boy receive, then the range of X is
View SolutionMatch the locus of the points in List-I with the curves in List-II (Here, p.4 and r are constants and `t, theta` and `lamda` are parameters)
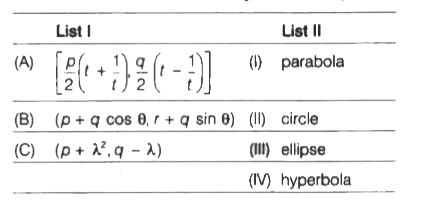
The correct match is
View SolutionWhen the origin is shifted to (1, -2) by translation of coordinate axes, the transformed coordinates of (3.-2) are `(alpha , beta)` If the axes are rotated about origin through an angle of `45^@` after the translation, then the transformed coordinates of `(alpha , beta)` are
View SolutionIf a straight line is passing through the point of intersection of the lines 3x - 4y + 1 = 0, 5x + y - 1 = 0 and making equal non-zero intercepts on the coordinate axes, then the area (in sq. units) of the triangle formed by this line with the coordinate axes, is
View SolutionIf the equations of the perpendicular bisectors of the sides AB and AC of a `Delta` ABC are x - y + 5 = 0 and x + 2y =0 respectively and if A is (1,-2), then the equation of the perpendicular bisector of the side BC is
View SolutionIf the lines x + 3y - 5 = 0 , 5x +2y-12 = 0 and 3x -ky-1=0 do not form a triangle, then a value of k is
View SolutionIf the combined equation of the diagonals of the square formed by the pairs of lines xy + 4x - 5y - 20 = 0 and xy - 5x + 4y - 20 =0 is `x^2-y^2-kx + ly = 0 ` , then k+l =
View SolutionThe equation of the pair of bisectors of the angle between the pair of straight lines `3x^2 + 7 xy + 2y^2 + 5x + 5y + 2 =0 ` is
View SolutionIf ` x = (2at)/(1 + t^2) , y = (a(1-t^2) )/(1 + t^2)` , where t is a parameter, then a is
View SolutionConsider the following statement :
I. `P(x_1, y_1)` and `Q (x_2, y_2)` are conjugate points with respect to the circle
` x^2 + y^2 + 2gx + 2fy + c= 0 ` then
`x_1 x_2 + y_1y_2 + g ( x_1 + x_2) + f ( y_1 + y_2) + c = 0`
II. The pole of the line x + y + 1 =0 with respect to the circle `x^2 + y^2 = 9` is (9.9).
Then, which one of the following is true?
View SolutionIf p is the point of contact of the circles
`x^2 + y^2 + 4x + 4y - 10 = 0 ` and
`x^2 + y^2 - 6x - 6y + 10` = 0 ` and Q is their external centre of similitude, then the equation of the circle with P and Q as the extremities of its diameter is
View Solutionlet `k gt 0 , s_alpha -= x^2 + y^2 + 2alpha x + k = 0 " and " s_beta -= x^2 + y^2 + 2 beta y - k = 0` . Then match the items of List -I with those of List - II

The correct match is
View SolutionThe equation of the circle touching the line 2x + 3y + 1 = 0 at the point (1,-1) and orthogonal to the circle which has the line segment having end points (0, -1) and (-2,3) as diameter, is
View SolutionThe angle between the tangents drawn from the point (1,4) to the parabola `y^2 = 4x ` is
View SolutionIf the line `y = - x + k` is normal to the curve `y^2 = 16x` , then k is
View SolutionThe normal drawn at the point
` ( sqrt(9) cos (pi/4) , sqrt(7) sin (pi/4)` to the ellipse `(x^2)/(9) + (y^2)/(7) = 1`
intersects its major axis at the point
View SolutionIf (1, - 2) is the focus and x + y - 2 = 0 is the directrix of the ellipse
`17x^2 - 2xy + 17x^2 - 32x + 76x + 86 - 0 ` , then its eccentricity is
View SolutionThe line 2x + y =1 is a tangent to the hyperbola `(x^2)/(a^2) - (y^2)/(b^2) = 1 (a gt b)` . If this line passes through the point of intersection of a directrix and the positive X-axis, then the eccentricity of that hyperbola is
View SolutionIf the orthocentre and the centroid of a triangle are at (5, 2, -6) and (9, 6, -4) respectively, then its circumcentre is
View SolutionIf the direction ratios of two lines are given by a + 2b + c = 0 and 11 bc +6ca - 14 ab = 0 . then the angle between these lines is
View SolutionA plane cuts the coordinate axes X,Y,Z at A,B,C respectively such that the centroid of the `Delta ABC` is (6,6,3). Then the equation of that plane is
View Solution`lim_(xtooo) x (log ( 1+ x/2) - "log"x/2) = `
View SolutionThe set of values of x for which the function `f(x) = log ( (x - 1)/(x + 2) )` is continous , is
View SolutionIf the function `f : R to R, ` defined by
`f(x) = {{:(5-3x " , if" x le (5)/(3) ) , (" " ", then 'f' is "), (x^(2) - 3x + 20 ", if " x gt (5)/(3)):}`
View SolutionIf t is a parameter and ` x = t + 1/t , y = t - 1/t , " then " (d^2 y)/(dx^2) = `
View SolutionIf ` ax^2 + 2hxy - by^2 = 3` then ` (d^2y)/(dx^2)` =
View SolutionIf the error in measuring the side l of an equilateral triangle is 0.01, then the percentage error in the area of the triangle, in terms of its side l is
View SolutionIf at any point `(x_1, y_1)` on the curve y=f(x) the lengths of the subtangent and subnormal are equal, then the length of the tangent drawn to that curve at that point is
View SolutionThe height of a right circular cylinder is decreasing while is diameter is increasing at a rate of 4 cm/see so as to keep its volume unchanged, the rate of change in its lateral surface area (in `cm^2` /sec) at the instant when its diameter is 8 cm and height is 12 cm, is
View SolutionIf x + y = 60 , x > 0 , y > 0 , then the maximum value of `xy^3` is
View Solution`int sqrt(1 + 2 cot x ( cot x + cosecx ) ) dx` =
View SolutionIf` int e^(alpha x) ( ( 1- beta sin x )/(1 - cos x ) ) dx = -e^x cot x/2+c, ` then
` (alpha^2 + beta^2)/(2 alpha beta)` =
View Solution`int (2x^2 - 4x^2 - x - 3 )/(x^2 - 2x - 3) dx = `
View Solution`int cosec^5 x dx = `
View Solution`int_(1/3)^(3) 1/x sin (1/x - x) dx = `
View Solution`int_(-1)^(3/2) | x sin (pi x ) | dx = `
View SolutionArea of the region (in square units) bounded by the curve y = `x^2 + 4` and the line y = 5x - 2 is
View SolutionIf m and n are the order and degree of the differential equation of the family of parabolas with focus at the origin and X-axis as its axis, then mn - m + n =
View SolutionThe solution of defferential equation
`(dy)/(dx) + x/y. (x^2 + y^2 - 1)/(2(x^2 + y^2) + 1) = 0 ` is
View SolutionIf `x " log " x (dy)/(dx) + y = log x^2 " and " y ( e) = 0 ` , then
`y(e^2)= `
View Solution
MATHEMATICS questions and complete solutions for chapter TS EAMCET 2019 (4 MAY SHIFT 2) of TS EAMCET PREVIOUS YEAR PAPERS of Class 12