Complete Solutions to QUESTION BANK of chapter RELATIONS AND FUNCTIONS of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | RELATIONS AND FUNCTIONS |
| V PUBLICATION | QUESTION BANK |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
Let P={1,2,3} , Q={a, b} Find P x Q and Q x P
View SolutionA={p, q, r}, B={m}
Wrițe 'A x B' and all subs of 'A x B'.
View SolutionLet `A` be the set of all students of a boys school. Show that the relation `R` in `A` given by `R`={(a, b): a is sister of b} is the empty relation and `R'`={(a, b): the difference between heights of a and b is less than 3 meters} is the universal relation.
View SolutionLet `"T"` be the set of all triangles in a plane with `"R"` as relation in `"T"` given by `"R"={("T"_1," T"_2): T_1~="T"_2}` . Show that `"R"` is an equivalence relation.
View SolutionLet L be the set of all lines in a plane and R be the relation in L defined as `R={(L_1,""""L_2): L_1(" i s p e r p e n d i c u l a r t o L")_2}` . Show that R is symmetric but neither reflexive nor transitive.
View SolutionShow that the relation `R` on the set `A={1,\ 2,\ 3}` given by `R={(1,\ 1),\ (2,\ 2),\ (3,\ 3),\ (1,\ 2),\ (2,3\ )}` is reflexive but neither symmetric nor transitive.
View SolutionShow that the relation `R` on the set `Z` of integers, given by `R={(a ,\ b):2` divides `a-b}` , is an equivalence relation.
View SolutionLet `R` be the relation defined on the set `A={1,\ 2,\ 3,\ 4,\ 5,\ 6,\ 7}` by `R={(a ,\ b):` both `a` and `b` are either odd or even}. Show that `R` is an equivalence relation. Further, show that all the elements of the subset {1, 3, 5, 7} are related to each other and all the elements of the subset {2, 4, 6} are related to each other, but no element of the subset {1, 3, 5, 7} is related to any element of the subset {2, 4, 6}.
View SolutionDetermine whether each of the following relations is reflexive, symmetric and transitive.
Relation R in the set
A = {1,2,,3,…,13,14} defined as R= {(x,y) : 3x -y = 0}
View SolutionShow that the relation R in the set R of real numbers, defined at `R={(a,b):a le b^(2)}` is neither reflexive nor symmetric nor transitive.
View SolutionCheck whether the relation R defined in the set `{1, 2, 3, 4, 5, 6}`as `R = {(a , b) : b = a + 1}`is reflexive, symmetric or transitive.
View SolutionShow that the relation `R` on `R` defined as `R={(a ,\ b): alt=b}` , is reflexive and transitive but not symmetric.
View SolutionCheck whether the relation `R` on `R` defined by `R={(a ,\ b): alt=b^3}` is reflexive, symmetric or transitive.
View SolutionShow that the relation `R` on the set `A={1,\ 2,\ 3}` given by `R={(1,\ 2),\ (2,\ 1)}` is symmetric but neither reflexive nor transitive.
View SolutionShow that the relation `R` on the set `A` of all the books in a library of a college given by `R={(x ,\ y): x` and `y` have the same number of pages}, is an equivalence relation.
View SolutionShow that the relation `R` on the set `A={1,\ 2,\ 3,\ 4,\ 5}` , given by `R={(a ,\ b):|a-b|` is even }, is an equivalence relation. Show that all the elements of {1, 3, 5} are related to each other and all the elements of {2, 4} are related to each other. But, no element of {1, 3, 5} is related to any element of {2, 4}.
View SolutionShow that each of the relation R in the set `A={x in Z: 0 le xle12}`,given by
R = {(a,b) : |a-b| is a multiple of 4} is an equivalence relation. Find the set of all elements related to 1 in each case.
View SolutionGive an example of a relation which is symmetric but neither reflexive nor transitive.
View SolutionShow that the relation R. in the set A of all points in a place given by
R = {(P,Q): the distance of the points P from the point Q from the origin }, is an equivalence relation. Further show that the set of all points related to a point `p != (0,0)`is the circle passing through P with origin as centre.
View SolutionShow that the relation R. defined in the set A of all triangle as `R={(T_1,T_2):T_1`is similar to `T_2`,is an equivalence relation. Consider three right angled triangles `T_1`with sides 3,4,5,`T_2` with sides 5,12,13 and `T_3` with sides 6,8,10. Which triangle among `T_1,T_2` and` T_3` are related ?
View SolutionShow that the relation R defined in the set A of all polygons as
`R={(P_1,P_2): P_1`and `P_2` have the same number of sides },is an equivalence relation.What is the set of all elements in A related to the right angled triangle T with sides 3,4 and 5?
View SolutionLet L be the set of all line in XY place and R be the relation in L defined as` R = {(L_1,L_2):L_1` is parallel to `L_2`}Show that R is an equivalence relation. Find the set of all line related to the line y=2x+4
View SolutionLet R be the relation in the set {1,2,3,4,} given by R = {(1,2),(2,2),(1,1),(4,4),(1,3),(3,3),(3,2)}.Choose the correct answer. a) R is reflexive and symmetric but not transitive b) R is reflexive and transitive but not symmetric c) R is symmetric and transitive but not reflexive d) R is an equivalence relation
View SolutionLet R be the relation in the set N given by `R={(a,b):a=b -2,b gt 6}`
choose the correct answer
View SolutionLet A be the set of all 50 students of class X in a school. Let `f : A rarr N`
be function defined by f(x) = roll numbers of the student x. Show that
f is one-one but not onto
View SolutionThe function `f:NtoN` given by `f(x)=2x`
View SolutionProve that the function `f: R rarr R` given by `f(x)=2 x` is one-one and onto.
View SolutionShow that the function `f: N rarr N`, given by `f(1)=f(2)=1` and `f(x)=x-1`, for every `xgt2`, is onto but not one - one
View SolutionCheck the injective and surjective of the following functions : `f : R rarr R` given by `f(x) = x^2`
View SolutionShow that `f : N rarr N` given by
`f(x) = { ((x +1), if x is odd), ((x - 1), if x is even) :}`
is both one-one and onto.
View SolutionCheck the injectivity and surjectivity of the following functions
`f:NtoN` defined by `f(x)=x^3`
View SolutionProve that the greatest integer function `f : R rarrR` given by `f(x) =[x]` is neither one-one nor onto, where [x] denotes the greatest integer less than or equal to x.
View SolutionShow that the modulus function `f: R rarr R` given by `f(x) = |x|`, is neither one-one nor onto.
View SolutionShow that the signum function `f : R rarr R` given by `f(x)= {(1,if x gt 0), (0, if x = 0), (-1, if x lt 0) :}` is neither one-one nor onto.
View SolutionLet A = {1, 2, 3}, B { 4, 5, 6} and let f = {(1,4),(2,5)(3,6)} be a function from A to B. Show that f is one-one.
View SolutionIn each of the following cases, states whether the function is one-one,
onto or bijective. Justify your answer. `f : R rarr R` defined by f(x) =3 - 4x
View SolutionLet A and B be sets. Show that
`f: AxxB to BxxA` such that
`f(a,b) = (b,a)` is a bijective function
View SolutionLet f: N to N be defined by
`f(n) = { (((n+1)/2)if n is odd), (n/2 if n is even) :}` for all `n in N`
State whether the function f is bijective. Justify yur answer.
View SolutionLet `A=R-{3}` and `B=R-{1}` Consider the function `f:ArarrB` defined by `f(x)=frac(x-2)(x-3)`
Is `f` one-one and onto? Justify your answer.
View SolutionLet `f:R rarrR` be defined as f(x) = `x^4` Choose the correct answer
View SolutionLet `f:R rarrR` be defined as f(x) = 3x Choose the correct answer
View SolutionLet `f:{2,3,4,5} rarr {3,4,5,9}` and `g:{3,4,5,9} rarr{7,11 , 15}` be functions defined as `f(2)=3`,` f(3) =4`, `f(4)=f(5)=5` and `g(3)=g(4)=7` and `g(5)=g(9)=11` . Find `gof`.
View SolutionFind `g o f` and `f o g`, if `f: R rarr R` and `g: R rarr R` are given by `f (x)=cos x` and `g(x)=3 x^2`. Show that `gof` `ne` `f o g`.
View SolutionShow that if `f: A rarr B` and `g: B rarr C` are one-one, then `gof : A rarr C` is also one-one.
View SolutionShow that if `f: A rarr B` and `g: B rarr C` are onto, then `gof : A rarr C` is also onto.
View SolutionAre 'f' and 'g' both necessarily onto, if gof, is onto?
View SolutionLet `f:{1 , 2,3 ,} rarr {a, b, c}` be one-one, and onto function given by `f(1)=a, f(2)=b` and `f(3)=c`. Shów that there exists a function `g:{a, b, c} rarr {1,2,3.}` such that `g o f=I_x` and `f o g=, I_ y` where, `X={1,2,3}` and `Y={a, b, c}`
View SolutionConsider `f : R rarr R` given f(x) = 4x + 3. Show that f is invertible. Find the inverse of f.
View SolutionConsider of `f : N rarrN` and `h : N rarr R` defined as f(x) = 2x, g(y) = 3y + 4
and h(z) = sin z,`AA`, x, y and z in N. Show that ho(gof) = (hog)of.
View SolutionLet S = {1, 2, 3}. Determine whether the function `f : S rarr S` defined as below have inverses. Find `f^(-1)`, if it exists
(a) f = {(1,1), (2,2), (3,3)}
(b) f = {(1,2), (2,1), (3,1)}
( c ) f = {(1,3), (3,2), (2,1)}
View SolutionLet f : {1, 3, 4} `rarr` {1, 2, 5} and
g : {1, 2, 5} `rarr` (1, 3} be given by
f = {(1,2), (3,5), (4,1)} and
g = {(1,3), (2,3), (5,1)}
Write down g o f
View SolutionLet f, g, and h be functions from R to R. Show that
`(f + g) o h = foh + goh`
View SolutionFind f o g and g o f
f(x) = |x| and g(x) = |5x -2|
View SolutionIf f(x) =`(4x + 3)/(6x - 4), x ne 2/3`, show that (fof)(x) = x, for all `x ne 2/3`.
What is the inverse of f ?
View SolutionState with reason whether the following functions have inverse
f : {1,2,3,4} to {10} with
f = {(1,10),(2,10),(3,10),(4,10)}
View SolutionShow that `f:[-1,1]toR` given by `f(x)=frac(x)(x+2)` is one-one.
View SolutionConsider `f : R rarr R` given f(x) = 4x + 3. Show that f is invertible. Find the inverse of f.
View SolutionConsider `f:R^+to[-5, infty)` given by
`f(x)=9x^2+6x-5`. Show that f is invertible with `f^-1(y)=frac(sqrt(y+6)-1)(3)`
View SolutionLet `f : X rarr Y` be invertible, show that f has unique inverse
View SolutionConsider f : {1, 2, 3} `rarr` {a, b, c} given by f(1) = a, f(2) = b and f(3) = c. find `f^(-1)` and show that `(f^(-1))^(-1)` = f
View SolutionLet `f : X rarr Y` be invertible, show that the inverse of `f^(-1)` = f,
i.e.,`(f^(-1))^(-1) = f`.
View SolutionIf `f : R rarr R` be given by f(x) = `(3 - x^3)^(1/3)`, then (f o f) (x) is
View Solutionf : `R - {(-4)/3} rarr R` be a function defined as `f(x) = (4x)/(3x +4)`. The inverse of f is the map g : Range `f rarr R - {(-4)/3}` given by
View SolutionCan you define a function from 'RxR rarr R' such as 'f_3: RxR rarr, R' defined by 'f_3(a, b)=a/b ?'
View SolutionCan yóu define a function from 'R xx R rarr R' such as 'f_4: R xx R rarr R' defined by 'f_4(a, b)=sqrt (a b)'
View SolutionShow that addition, subtraction and multiplication are binary operations on R, but division is not a binary operation on R. Further, show that division is a binary operation on the set R of nonzero real numbers.
View SolutionShow that subtraction and division are not binary operations on N.
View SolutionShow that *`: R xx R rarr R` is given by `(a, b) rarr(a+4 b)^2` is a binary operation.
View SolutionLet `P` be the set of all subsets of a given set X. Show that `uu: P xx P rarr P` given by `(A, B) rarr A uu B` and `nn: P xx P rarr P` given by `(A, B) rarr A nn B` are binary operations on the set `P`.
View SolutionShow that the `vee: R xx R rarr R` given by `(a, b) rarr max {a, b}` and the
*`: R xx R rarr R` given by `(a, b) rarr min {a , b}` are binary operations.
View SolutionShow that `+: R xx R rarr R` and `xx: R xx R rarr R` are commutative binary operaions, but `- : R xx R rarr R` and `-:: R_* xx R_* rarr R_*` are not commutative.
View SolutionShow that *`: R xx R rarr R` defined by a * b`=a+2 b` is not commutative.
View SolutionShow that addition and multiplication are associativé binary operation on `R`. But subtraction is not associative on `R`. Division is not associative on `R`.
View SolutionShow that * :`R xx R rarr R` given by `a`* `b= a+2 b` is not associative.
View SolutionShow that zero is the identity for addition on R and 1 is the identity for multiplication on `R`. But there is no identity element for the operations. `- : R xx R rarr R` and `-:: R. xx R_. rarr R_.`
View SolutionShow that `- a` is not the inverse of `a in N` for the addition operation '+' on `N` and `1/a` is not the inverse of `a in N` for multiplication operation 'X' on `N` for `a ne1`
View SolutionDetermine whether or not each of the definitions of `**` given below gives a binary operation. In the event that `**` is not a binary operation, give justification for this
on `Z^+`, define `**` by `a**b=|a-b|`
View SolutionFor each binary operation `**` defined below, determine whether `**` is commutative or associative
on Z, define `a**b=a-b`
View SolutionConsider the binary operation on a set `{1,2,3,4,5}`. defined by `a ^^ b=min {a, b}`. Write the operation table of the operation.
View SolutionConsider the binary operation `**` on the set A= {1,2,3,4,5} given by the following multiplication table
Compute `(2**3)**4` and `2**(3**4)`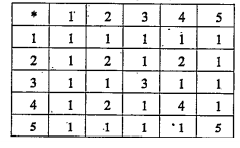
View SolutionLet `**`' be the binary operation on N given by `a**'b`= L.c.m. of a and b. Find `5**7, 20**16`
View SolutionConsider an operation `**` defined on the set
`A={1,2,4,8}` by `a**b=LCM` of a and b.
Show that `**` is a binary operation.
View SolutionLet `ast` be a binary operation on N defined by `aastb=HCF` of a and b
Is `ast` commutative?
View SolutionLet `**` be a binary operation on the set Q of rational numbers as follows
`a**b=a-b`.
Check whether * is commutative and associative
View SolutionLet
`A=NtimesN` and `ast`
be a binary operation on A defined by (a,b)*(c,d) = (a + c,b + d)
Prove that
`ast`
is associative
View SolutionState whether the following statements are true or false. Justify
For an arbitary binary operation `**` on N, `a**a=a AA a in N`
View SolutionConsider a binary operation `**` on N defined as `a**b=a^3+b^3`. Choose the correct answer. a) both associative and commutative b)commutative but not associative c) associative but not commutative d) neither commutative nor associative
View SolutionIf `R_1` and `R_2` are equivalence relations in a set A, show that `R_1 nn R_2` is also an equivalence relation.
View SolutionLet `X={1,2,3,4,5,6,7,8,9}`. Let `R_1` be a relation in `X` given by `R_1`={(x, y): x-y is divisible by 3} and `R_2` be another relation on `X` given by` R_2={(x, y):{x ,y} sub{1,4,7} `or `{x, y} sub {2,5,8}` or . `{x, y}sub {3,6,9}}`. Show that `R_1=R_2`
View SolutionLet `f: X rarr Y`, be a function. Define a relation `R` in `X` given by: `R={(a, b): f(a)=f(b)}` Examine if `R` is an equivalence relation.
View SolutionDetermine which of the following binary operation on the set R are associative and which are communtative.
`a ** b=1`
View SolutionFind the number of all one-one functions from set `A={1,2,3}` to itself.
View SolutionConsider the identity function, `I_N: N rarr N` defined as `I_n(x)=x forall x in N`. Show that although `I_N` is onto but `I_N+I_N: N rarr N` defined as.
`(I_N+I_N)(x)=I_N(x)+I_N(x)=x+x=2 x` is not onto
View SolutionConsider a function `f : [0, pi/2] rarr R`
given by f(x) = sin x and `g : [0, pi/2] rarr R`
given by g(x) = cos x. Show that f and g are one-one, but f + g is not one-one.
View SolutionLet `f:RrarrR` be defined as f(x) = 10x+7
Find the function `g:RrarrR` such that gof = fog = `I_R`
View SolutionLet `f:WrarrW` be defined as f(n) = n-1
if n is odd and
f(n) = n+1 if n is even.
Show that f is invertible. Find the inverse of f. Here W is the set of all whole numbers.
View SolutionIf `f:RrarrR` is defined by
`f(x) = x^2-3x+2`, find f(f(x))
View SolutionShow that the function `f:R rarr R` given by `f(x)=x^3` is injective.
View SolutionGiven a non empty set `X`, consider `P(X)` which is the set of all subsets of `X` . Define the relation R in `P(X)` as follows. For subsets A, B in `P(X)`, `A R B` if and only of `A sub B`. Is `R` an equivalence relation on `P(X)` . Justify your answer.
View SolutionFind the number of all onto functions from the set `{1,2,3 …... n}`to itself.
View Solution
QUESTION BANK questions and complete solutions for chapter RELATIONS AND FUNCTIONS of V PUBLICATION of Class 12