Complete Solutions to QUESTION BANK of chapter VECTOR ALGEBRA of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | VECTOR ALGEBRA |
| V PUBLICATION | QUESTION BANK |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
Represent graphically a displacement of `40 km, 30^circ` west of south.
View SolutionClassify the following, measures as scalars and vectors.
(i) 5 seconds
(ii) `1000 m^3`
(iii)`10 N`
(iv) `30( km`/` hr)`
(v) `10 (g `/` cm^3)`
(vi) `20 (m `/` s)` towards north
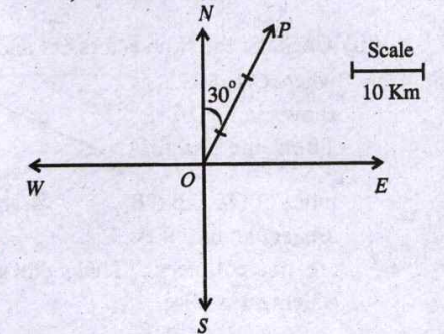
View SolutionRepresent graphically a displacement of `40 km,30^@` east of north.
View SolutionClassify the following measures as scalars and vectors.
i) `10 kg`
ii) `2` meters north-west
iii) `40^circ`
iv) `40` watt
v) `10^(-10)` coloumb
vi) `-20 m `/` s^2`
View SolutionClassify the following as scalar and vector quantities.
i) time period
ii) distance.
iii) force
iv) velocity
v) workdone
View SolutionAnswer the following as true or false.
i) `veca` and `-veca` are collinear
ii) Two collinear vectors are always equal in magnitude.
iii) Two vectors having same magnitude are collinear.
iv) Two collinear vectors having the same magnitude are equal.
View SolutionFind the values of `x, y` and `z` so that the vectors `veca=x hati+2 hatj+z hatk` and `vecb=2 hati+y hatj+hatk` are equal.
View SolutionLet `veca=hati+2 hatj` and `vecb=2 hati+hatj` . Is `|veca|=|vecb| ?`.Are the vectors `veca` and `vecb` equal?
View SolutionFind unit vector in the direction of vector `veca= 2 hati+3 hatj+hatk`
View SolutionFind a vector in the direction of vector `veca=hati-2 hatj` that has magnitude 7 units.
View SolutionFind the unit vector in the direction of the sum of the vectors,
`veca=2 hati+2 hatj-5 hatk` and `vecb=2 hati+2 hatj+3 hatk`
View SolutionWrite the direction ratio's of the vector, `veca=veci+hatj-2 hatk` and hence calculate its direction cosines.
View SolutionFind the vector joining the points `P(2,3,0)` and `Q(-1,-2,-4)`. directed from `P` to `Q`.
View SolutionConsider two points `P` and `Q` with position vectors `vec(OP)=3 veca-2 vecb` and `vec(OQ)=veca+vecb`. Find the position vector of a point `R` which divides the line joining `P` and `Q` in the ratio `2: 1`, i) Internally and ii) externally.
View SolutionShow that the vectors '2 hati-hatj+hatk, hati-3 hatj-5 hatk' and '3 hati-4 hatj-4 hatk' form the vertices of a right-angled triangle.
View SolutionCompute the magnitude of the following vectors.
`veca=hati+hatj+hatk, vecb=2 hati-7 hatj-3 hatk`
`vecc=1/(sqrt3) hati+1/(sqrt3) hatj-1/(sqrt3) hatk`
View SolutionWrite two different vectors having same magnitude.
View SolutionWrite two different vectors having same direction.
View SolutionFind the values of `x` and `y` so that the vectors `2 hati+3 hatj` and `x hati+y hatj` are equal.
View SolutionFind the scalar and vector components of the vector with initial point (2,1)
and terminal point(-5,7).
View SolutionFind the sum of the vectors.
`veca=hati-2 hatj+hatk, vecb=-2 hati+4 hatj+5 hatk` and `vecc=hati-6 hatj-7 hatk`
View SolutionFind the unit vector in the direction of the vector `veca=hati+hatj+2 hatk`
View SolutionFind the unit vector in the direction of vector `vecP Q`, where `P` and `Q` are the points `(1,2,3)` and `(4,5,6)` respectively.
View SolutionFor given vectors, `veca=2 hati-hatj+2 hatk` and `vecb=-hati+hatj-hatk` , find the unit vector in the direction of the vectors `veca+vecb`
View SolutionFind a vector in the direction of vector `5 hati-hatj+2 hatk` which has magnitude 8 units.
View SolutionShow that the vectors `2 hati-3 hatj+4 hatk` and `-4 hati + 6 hatj-8 hatk` are collinear.
View SolutionFind the direction cosines of the vector `hati+2 hatj+3 hatk`
View SolutionFind the, direction cosines of the vector joining 'A(1,2,-3)' and 'B(-1,-2,1)', directed from 'A' fò 'B'.
View SolutionShow that the vector `overset^^i+overset^^j+overset^^k` is equally inclined to the axes OX,OY and OZ.
View SolutionFind the position vector of a point `R` which divides the line joining two points `P` and `Q` whose position vectors are `hati+2 hatj-hatk` and `-hati+hatj+hatk` respectively, in the ratio `2: 1`
(i) internally (li) externally.
View SolutionFind the position vector of the mid point of the vector joining the points
P(2,3,4)and Q(4,1,-2).
View SolutionShow that the points A, B and C with position vectors `veca=3i-4j-4k,vecb=2i-j+k` and `vecc=i-3j-5k` respectively form the vertices of a right angled triangle.
View SolutionIn triangle 'ABC', which of the following is not true.
`(##VPU_HSS_MAT_XII_C10_E03_020_Q01##)`
View SolutionIf `oversetrarra"and"oversetrarrb`are two collinear vectors, then which of the following are incorrect: a)`oversetrarrb =oversetrarra lambdascalar"lambda` b) `oversetrarra = +-oversetrarrb` c)The respective components of `oversetrarra "and "oversetrarrb` are proportional d)Both `oversetrarra"and" oversetrarrb` have same direction, but different magnitude.
View SolutionFind the angle between two vectors `veca` and `vecb` with magnitudes 1 and 2 respectively and when `veca . vecb=1`
View SolutionFind the angle between the vectors `veca=hati+hatj-hatk` and `vecb=hati-hatj+hatk`
View SolutionIf `veca=5i-j-3k` and `vecb=i+3j+5k`,then show that the vectors `veca+vecb`,`veca-vecb` are perpendicular.
View SolutionFind the projection of the vector `veca=2 hati+3 hatj+2 hatk` on the vector `vecb=hati+2 hatj+hatk`.
View SolutionFind `|veca-vecb|`, if two vectors `veca` and `vecb` are such that `|veca|=2,|vecb|=3` and `veca. vecb=4`
View SolutionIf `veca` is a unit vector and `(vecx-veca) .(vecx+veca)=8`, then find `|vecx|`.
View SolutionFor any two vectors `veca` and `vecb`, we always have `|veca+vecb| le|veca|+|vecb|` (triangle ineuality)
View SolutionShow that the points `A(-2 hati+3 hatj+5 hatk)`, `B(hati+2 hatj+3 hatk)` and `C(7 hati-hatk)` are collinear.
View SolutionFind the angle between two vectors`oversetrarra"and"oversetrarrb` with magnitudes `sqrt3"and"2` respectively having`oversetrarra.oversetrarrb=sqrt6`.
View SolutionFind the angle between the vectors `hati-2 hatj+3 hatk` and `3 hati-2 hatj+hatk`
View SolutionFind the projection of the vector `hati-hatj` on the vector `hati+hatj`.
View SolutionFind the projection of a vector `i+3j+7k` on the vector `7i-j+8k`.
View SolutionShow that each of the given three vectors is a unit vector :`1/7(2overset^^i+3overset^^j+6overset^^k),1/7(3overset^^i-6overset^^j+2overset^^k),1/7(6overset^^i+2overset^^j-3overset^^k)`.
Also, show that the are mutually perpendicular to each other.
View SolutionFind `|veca|` and `|vecb|`, if `(veca+vecb) .(veca-vecb)=8` and `|veca|=8|vecb|`
View SolutionEvaluate the product `(3 veca-5 vecb) .(2 veca+7 vecb)`
View SolutionFind the magnitude of two vectors `oversetrarra"and"oversetrarrb,` having the same magitude and such that the angle between them is `60^@` and their scalar product is `1/2`.
View SolutionFind `|vecx|`, if for a unit vector `veca,(vecx-veca) .(vecx+veca)`=12'
View SolutionIf`" " oversetrarra=2overset^^i+2overset^^j+3overset^^k," "` `oversetrarrb= -overset^^i+2overset^^j+overset^^k " and " oversetrarrc = 3overset^^i+overset^^j` are such that `oversetrarra+lambda oversetrarrb` is perpendicular to `oversetrarrc`,then find the value of `lambda`
View SolutionShow that`""|oversetrarra|oversetrarrb +|oversetrarrb| oversetrarra""` is perpendicular to `|oversetrarra|oversetrarrb-|oversetrarrb| oversetrarra,` for any two non-zero vectors.
View SolutionIf `veca.veca=0` and `veca. vecb=0`, then what can be concluded about the vector `vecb` ?
View SolutionIf `veca, vecb, vecc` are unit vectors such that
`veca+vecb+vecc=0`, find the value of
`veca.vecb+vecb.vecc+vecc.veca`.
View SolutionIf either `veca=vec0"or" vecb =vec0, "then"vecaxxvecb=vec0`.Is the converse true? Justify your answer with an example.
View SolutionIf the vertices A,B,C of a triangle ABC are (1,2,3),(-1,0,0),(0,1,2)respectively,then find `/_ABC.`

View SolutionUsing vectors, show that the points
`A(1,2,7),B(2,6,3),C(3,10,-1)` are collinear.
View SolutionShow that the vectors `2 hati-hatj+hatk, hati-3 hatj-5 hatk` and `3 hati-4 hatj-4 hatk` form the vertices of a right-angled triangle.
View SolutionIf a is a non-zero vector of magnitude'a' and `lambda` a non-zero scalar, then `lambda oversetrarra` is a unit vector if: a)`lambda = 1` b)`lambda = -1` c)`a=|lambda|` d)`a =1/(|lambda|)`
View SolutionShow that the area of a parallelogram with diagonals `veca` and `vecb` is `1/2|veca xx vecb|`
View SolutionFind `|veca xx vecb|` if `veca=2 hati+hatj+3 hatk` and `vecb=3 hati+5 hatj-2 hatk`
View SolutionFind a unit vector perpendicular to each of the vectors `(veca +vecb)` and `(veca-vecb)`, where `veca=hati+hatj+hatk, vecb=hati+2 hatj+3 hatk`
View SolutionConsider the triangle ABC with vertices A(1,1,1), B(1,2,3) and C(2,3,1).Hence find the area of the triangle.
View SolutionFind the area of a parallelogram whose adjacent sides are given by the vectors `veca=3 hati+hatj+4 hatk` and `vecb=hati-hatj+hatk`
View SolutionFind `|veca xx vecb|`, if. `veca=hati-7 hatj+7 hatk` and `vecb=3 hati-2 hatj+2 hatk`
View SolutionFind a unit vector perpendicular to each of the vector `veca+vecb`, and `veca-vecb`, where `veca=3 hati+2 hatj+2 hatk` and `vecb=hati+2 hatj-2 hatk`
View SolutionChoose the correct answer from the backet. If a unit vector `hata` makes angles `pi/4` with i and `pi/3` with j and acute angle `theta` with k.
then `theta` is
View SolutionShow that `(veca-vecb) xx(veca+vecb)=2(veca xx vecb)`
View SolutionFind `lambda`and `mu` if
`(2overset^^i+6overset^^j+27overset^^k)xx(overset^^i+lambdaoverset^^j+muoverset^^k)=oversetrarr0`.
View SolutionGiven that `oversetrarra.oversetrarrb=0"and"oversetrarraxxoversetrarrb=oversetrarr0`.What can you conclude about the vectors `oversetrarra" and "oversetrarrb.`
View SolutionLet the vectors 'veca, vecb, vecc' be given as 'a_1 hati+a_2 hatj+a_3 hatk, b_1 hati+b_2 hatj+b_3 hatk, c_1 hati+c_2 hatj+c_3 hatk', Then show that 'veca xx(vecb+vecc)=veca xx vecb+veca xx vecc'
View SolutionIf either `veca=vec0"or" vecb =vec0, "then"vecaxxvecb=vec0`.Is the converse true? Justify your answer with an example.
View SolutionFind the area of the triangle with vertices A(1,1,2),B(2,3,5) and C(1,5,5).
View SolutionFind the area of the parallelogram whose adjacent sides are determined by the vectors 'veca=hati-hatj+3 hatk' and 'vecb=2 hati-7 hatj+hatk'
View SolutionLet the vectors`veca"and"vecb`be such that
`|veca|=3"and"|vecb|=sqrt2/3`,then `vecaxxvecb ` is a unit vector, if the angle between `veca"and"vecb`is : a)`pi/6` b)`pi/4` c)`pi/3` d)`pi/2`
View SolutionArea of a rectangle having vertices 'A, B, C' and 'D' with position vectors '-hati+1/2 hatj+4 hatk', 'hati+1/2 hatj+4 hatk, hati-1/2 hatj+4 hatk' and '-hati-1/2 hatj+4 hatk' respectively is
View SolutionIf `hati+hatj+hatk, 2 hati+5 hatj, 3 hati+2 hatj-3 hatk` and `hati-6 hatj-hatk` are the position vectors of points `A, B , C` and `D` respectively, then find the angle between `bar(AB)` and `bar(CD)`. Deduce that `bar(AB)` and `bar(CD)` are collinear.
View SolutionLet `veca,vecb, " and " vecc` be three vectors such that `|veca|=3,|vecb|=4,|vecc|=5` and each
one of the being perpendicular to the sum of the other two, find `|veca+vecb+vecc|.`
View SolutionThree vectors `veca,vecb,"and" vecc` satisfy the condition`veca+vecb+vecc=vec0`. Evaluate the quantity `mu=veca.vecb+vecb.vecc+vecc.veca`. If `|veca|=1,|vecb|=4 " and " |vecc|=2`.
View SolutionWrite down a unit vector in XY plane making an angle of `30^@`
with the positive direction of x-axis.
View SolutionFind the scalar components and magnitude of the vector joining the points
`P(x_1,y_1,z_1)`and `Q(x_2,y_2,z_2).`
View SolutionIf 'veca=vecb+vecc', then is it true that '|veca|=|vecb|+|vecc| ?' Justify your answer.
View SolutionFind the value of 'x' for which 'x(hati+hatj+hatk)' is a unit vector.
View SolutionFind a vector of magnitude 5 units and parallel to the resultant of the vectors `veca=2overset^^i+3overset^^j-overset^^k "and "vecb=overset^^i-2overset^^j+overset^^k`.
View Solutionif `veca=hati+hatj+hatk, vecb=2 hati-hatj+3 hatk` and `vecc=hati-2 hatj+hatk`, find a unit vector parallel to the vector `2 veca-vecb+3 vecc`
View SolutionShow that the points
A(1,-2,-8),B(5,0,-2)andC(11,3,7)are collinear and find the ratio in which B divides AC.
View SolutionFind the position vector of a point `R` which divides the line joining two points `P` and `Q` whose position vectors are `(2 veca+vecb)` and `(veca-3 vecb)` externally in the ratio `1: 2` Also show that `P` is the mid point of the line segment RQ.
View SolutionThe two adjacent sides of a parallelogram are '2 hati-4 hatj+5 hatk' and 'hati .-2 hatj-3 hatk .' Find the unit vector parallel to its diagonal. Also find its,area.
View SolutionShow that the direction cosines of a vector equally inclined to the axes `O X, OY` and `O Z` are `1/(sqrt3), 1/(sqrt3), 1/(sqrt3)`
View SolutionLet ' veca=hati+4 hatj+2 hatk, vecb=3 hati-2 hatj+7 hatk' and 'vecc=2 hati-hatj+4 hatk'. Find a vector 'd' 'which is perpendicular to both 'veca' and 'vecb', and 'vecc . vecd=15'
View SolutionThe scalar product of the vector `hati+hatj+hatk` with a unit vector along the sum of vectors `2 hati+4 hatj-5 hatk` and `lambda hati+2 hatj+3 hatk` is equal to one. Find the value of `lambda`
View SolutionIf `veca, vecb, vecc` are mutually perpendicular vectors of equal magnitudes, show that the vector `veca+vecb+vecc` is equally inclined to `veca, vecb` and `vecc`
View SolutionProve that
`(veca+vecb).(veca+vecb)=|veca|^2+|b|^2` if and only if `veca,vecb` are perpendicular, given
`veca!=vec0"and"vecb!=0`.
View SolutionChoose the correct answer. If `theta` is the angle between two vectors `veca"and"vecb`, then `veca.vecb ge 0` only when a)`0 lt theta lt pi/2` b)`0 le theta le pi/2` c)`0 lt theta lt pi` d)` 0 le theta le pi`
View SolutionLet 'veca' and 'vecb' be two unit vectors and 'theta' is the angle between them. Then 'veca,+vecb' is a unit vector if
View SolutionThe value of `hati.(hatj xx hatk)+hatj.(hati xx hatk)+hatk.(hati xx hatj)` is a)0 b)-1 c)1 d)3
View SolutionIf `theta` is the angle between any two vectors `veca` and `vecb`, then `|veca.vecb|=|veca xx vecb|` when `theta` is equal to a)0 b)`pi/4` c)`pi/2` d)`pi`
View SolutionProve that the Iine joining the midpoints of the two sides of a triangle is parallel to the third side and half of its length.
View SolutionFind the projection of vector `hati-hatj` on the vector `hati+hatj`
View Solution
QUESTION BANK questions and complete solutions for chapter VECTOR ALGEBRA of V PUBLICATION of Class 12