Complete Solutions to QUESTION BANK of chapter LINEAR PROGRAMMING of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | LINEAR PROGRAMMING |
| V PUBLICATION | QUESTION BANK |
| Number Of Questions | 39 |
| Academic Year | 2023-24 |
Consider the linear programming problem:
Maximize `z=4x+y`
Subject to constraints:
`x+yle50`,`3x+yle90`,`x,yge0`
Draw the feasible region.
View SolutionSolve the following linear programming problem graphically. Minimise `Z=200 x+500 y` subject to the constraints: `x+2 y ge 10`, `3 x+4 y le 24`, `x ge 0, y ge 0`
View SolutionSolve the following problem graphically.
Minimise and Maximise `Z=3 x+9 y`
subject to the constraints: `x+3 y le 60`, `x+y ge 10`, `x leq y`, `x ge 0, y ge 0`
View SolutionDetermine graphically the minimum value of the objective function `Z=-50 x+20 y` subject to the constraints: `2 x-y ge -5`, `3 x+y ge 3`, `2 x-3 y le 12`, `x ge 0, y ge 0`
View SolutionMinimise `Z=3 x+2 y`,subject to the constraints: `x+y ge 8`, `3 x+5 y le 15`, `x ge 0, y ge 0`
View SolutionSolve the following linear programming problems graphically. Maximise z = 3x + 4y subject to the constraints: `x + y le 4, x ge 0, y ge 0`.
View SolutionConsider the linear programming problem:
Minimise `Z=-3x+4y`
Subject to `x+2yle8`,`3x+2yle12`,x,y`ge`0`
Find the corner at which Z attain its minimum.
View SolutionMaximise `Z=5 x+3 y` Subject to `3 x+5 y le 15,5 x+2 y le 10, x ge 0, y ge 0`
View SolutionMinimise `Z=3 x+5 y`
such that `x+3 y ge 3, x+y ge 2, x, y ge 0`
View SolutionConsider the LPP
Maximise `z=3x+2y`
Subject to the constraints
`x+2yle10`,3x+y`le`15`,`x,y`ge`0`
Find the maximum value of Z.
View SolutionSolve the following linear programming problems graphically
Minimize Z = x + 2y
Subject to `2x + y ge 3, x + 2y ge 6 , x ge 0, y ge 0`
View SolutionShow that the maximum of `Z` occurs at more than two points.
Minimise and Maximise `Z=5 x+10 y `. Subject to `x+2 y le 120, x+y ge 60, x-2 y ge 0, x, y ge 0`
View SolutionMinimize and maximize z = x + 2y subject to `x + 2y ge 100, 2x - y le 0 , 2x + y le 200, x , y ge 0`.
View SolutionMaximise `z=-x+2 y` subject to the constraints: ` x ge 3, x+y ge 5, x+2 y ge 6, y ge 0`
View SolutionMaximise z = x + y, subject to `x - y le -1 , -x + y le 0, x , y ge 0`.
View SolutionA manufacture company makes two models `A` and `B` of a product. Each piece of model `A` requires 9 labour hours for fabricating and 1 labour hour for finishing and `B` requires 12 labour hours for fabricating and 3 labour hours for finishing. For fabricating and finishing the maximum labour hours available are 180 and 30 respectively per week. The company makes a profit of Rs. 8000/- on each piece of Model `A` and Rs. 12000/- on each piece of Model B. How many piece of Model `A` and `B` should be manufactured per week to realise a maximum profit? What is the maximum profit per week?
View SolutionOne kind of cake requires 200g of flour and 25g of fat ,and another kind of cake requires 100g of flour and 50g of fat.Find the maximum number of cakes which can be made from 5kg of flour and 1kg of fat assuming that there is no shortage of the other ingredients,used in making the cake.
View SolutionA factory makes tennis rackets and bats,A tennis racket takes 1.5 hours of machine and 3 hours of craftsman's time in its making,while a cricket bat takes 3 hours of machine time and 1 hour of craftman's time.In a day,the factory has availibilityof not more than 42 hours of machine time and 24 hours of craftman's time.
What no of rackets and bats must be produced if the factory is to work at full capacity?
View SolutionA manufacturur produces nuts and bolts.It takes 1 hour of work on machine A and 3 hours on machine B to produce a package of nuts. It takes 3 hours on machine A and 1 hour on machine B to produce a package of bolts.He earns a profit of Rs.17.50 per package on nuts and Rs.7 per package on bolts.How many package of each should be produced each day so as to maximise the profit,if he operates his machine for at the most 12 hours a days?
Solve the LPP graphically and find the number of packages of nuts and bolts to be manufactured.
View SolutionA factory manufactures two types of screws, `A` and `B`. Each type of screw requires the two machines, an automatic and a hand operated.It takes `4` minutes on the automatic and `6` minutes on hand operated machines to manufacture a package of screws A, while it takes `6` minutes on automatic and `3` minutes on the hand operated machines to manufacture a package of screws B. Each machine is available for at the most `4` hours on any day. The manufacturer can sell a package of screw `A` at a profit of Rs `7` and screws `B` at a profit of Rs `10` . Assuming that he can sell all the screws he manufactures, how many packages of eách type should the factory owner produce in a day in order to maximise his profit? Determine the maximum profit.
View SolutionA cottage industry manufactures pedestal lamps and wooden shades, each requiring the use of a grinding/cutting machine and a sprayer. It takes 2 hours on grinding/cutting machine and 3 hours on the sprayer to manufacture a pedestal lamp. It takes 1 hour on the grinding/cutting machine and 2 hours on the sprayer to manufacture a shade. On any day, the sprayer is available for at the most 20 hours and the grinding/cutting machine for at the most 12 hours. The profit from the sale of a lamp is Rs.5 and that from a shade is Rs.3. Assuming that the manufacturer can sell all the lamps and shades that he produces, how should he schedule his daily production in order to maximise his profit?
View SolutionA company manufactures two types of rovelty souvenirs made of plywood. Souvenirs of type A require `5` minutes each for cutting and `10` minutes each for assembling. Souvenirs of type `B` require `8` minutes each for cutting and `8` minutes each for assembling. There are 3 hours 20 minutes available for cutting and 4 hours for assembling. The profit is Rs `5` each for type `A` and Rs `6` each for type `B` souvenirs. How many souvenirs of each type should the company manufacture in order to maximise the profit?
View SolutionA merchant plans to sell twó types of personal computers - a desktop model and a portable model that, will cost Rs `25000` and Rs. `40000` respectively. He estimates that the total monthly demand of computers will not exceed `250` units. Determine the number of units of each type of computers which the merchant should stock to get maximum profit if he does not want to invest more than Rs `70` lakhs and if his profit on the.desktop model is Rs `4500` and on portable model is Rs `5000` .
View SolutionA diet is to contain atleast 80 units of vitamin A and 100 units of minerals.Two foods F1 and F2 are available.Food F1 costs Rs 4 per unit food and F2 costs Rs 6 per unit.One unit of food F1 contains 3 units of vitamin A and 4 units of minerals.One unit of food F2 contains 6 unit of of vitamin A and 3 units of minerals.Formulate this as a linear programming problem.Find the minimum costs for diet that consists of misture of these two foods and also meets the minimal nutritional requirements.
View SolutionThe corner points of the feasible region determined by the following system of inequalities: `2 x+y le 10, x+3 y le 15, x, y ge 0` are `(0,0),(5,0),(3,4)`, and `(0,5)`. Let `Z=p x+q y`, where `p, qgt0`. Condition on `p` and `q` so that the maximum of `Z` occurs at both `(3,4)` and `(0,5)` is a)`p=q` b)`p=2q` c)`p=3q` d)`q=3p`
View Solution(Manufacturing problem) A manufacturer has three machines I , II and III installed in his factory. Machines I and II are capable of being operated for at most 12 hours where as machine III must be operated for atleast 5 hours a day. She produces only two items M and N each requiring the use of all the three machines. The number of hours required for producing 1 unit of each of M and N on the three machines are given in the following table:
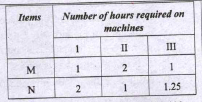
She makes a profit of Rs 600 and Rs 400 on items M and N respectively. How many of each item should she produce so as to maximise her profit assuming that she can swll all the items that she produced ? What will be the maximum profit ?
View SolutionHow many packets of each food should be used to maximise the amount of vitamin A in the diet? What is the maximum amount of vitamin 'A' in the diet?
View SolutionAn aeroplane can carry a maximum of 200 passengers. A profit of Rs 1000 made on each executive class ticket and a profit of Rs 600 is made on economy class ticket. The airline reserves atleast 20 seats for executive class. However, at least 4 times as many passengers prefer to travel by economy class than by the executive class. Determine how many tickets of each type sold in order to maximise the profit for the airline. What is the maximum profit?
View SolutionTwo godowns A and B have grains capacity of 100 quintals and 50 quintals respectively.They supply to 3 ration shop D,E,F whose requirement are 60,50 and 40 quintals respectively.The cost of transportation per quintal from the godowns to the shops is given in the following table,
transportation cost per quintal(in Rs).
Hence should the supplies be transported in order that the transportation cost is minimum?What is the minimum cost?

View SolutionIf the grower wants to maximise the amount of nitrogen added to the garden, how many bags of each brand should be added? What is the maximum amount of nitrogen added?
View SolutionA dealer wishes to purchase a number of fans and sewing machines. He has only Rs. 5760 to invest and has space for at most 20 items. A fan costs him Rs. 360 and a sewing a machine Rs. 240. His expectation is that he can sell a fan at a profit Rs. 22 and a sewing machine at a profit of Rs. 18 . Assuming that he can sell all the items that he can buy,how should he invest his money in order to maximise the profit? Formulate this as a linear programming problem and solve graphically.
View SolutionA furniture dealer deals only in two items - tables and chairs. He has Rs. 5000 to invest and a space to store at most 60 pieces. A table costs him Rs. 250 and a chair Rs. 50 . He can sell a table at a profit of Rs. 50 and a chair at a profit of Rs.15 .Assume that he can sell all items that he buys. Using linear programming, formulate the problem for maximum profit.
View SolutionA company produces two types of goods, `A` and `B`, that require gold and silver. Each unit of type `A` requires `3 gm` of silver and `1 gm` of gold while that of type `B` requires `1 gm` of silver and `2 gm` of gold. The company can use `9 gm` of silver and `8 gm` of gold. If each unit of type `A` brings a profit of Rs. `40` and that of type B Rs. `50`, find the number of units of each type that the company should produce to maximise the profit. What is the maximum profit.
View SolutionIf a young man rides his motor cycle at `25 k . p . h`, he has to spend Rs. `2 per km` on petrol, if he rides it at ạ faster speed of `40k.p.h.`, the petrol cost increases to Rs. `5 per k m`. He has Rs. `100` to spend on petrol and wishes to find what is the maximum distance, he can travel within the hour. Express this as a linear programming problem and then solve it.
View SolutionA firm deals with two kinds of fruit juices-pineapple and the, orange juice. These are mixed and two types of mixtures are obtained which is sold as soft drinks `A` and `B`, One tin of `A` need `4` litres of pineapple juice and `1` litre of orange juice. One tin of `B` needs `2` litres of pineapple and `3` litres of oranges juice. The firm has only `46` litres of pineapple juice and `24` litres of orange jụice. Each tin of `A` and `B` is sold at a profit of Rs.` 4` /- and Rs. `3` /-respectively. How many tins of `A` and `B` should the firm produce to maximise profiț? Formulate the linear programming problem and solve it graphically.
View SolutionA firm manufactures two types of products `A` and `B` and sells them at a profit of Rs. `5` per unit of type A and Rs. `3` per unit of type `B`. Each product is processed on two machines `M_1` and `M_2`. One unit of type A requires one minute of processing time, on, `M_1` and two minutes of processing time on `M_2` whereas one unit of type `B` requires one minute of processing time on `M_1` and one minute of `M_2`. Machines `M_1` and `M_2` are respectively available for at most `5` hours and `6` hours a day. Find how many, units of each type of product should the firm produce a day, in order, to maximise the profit. Solve thè problem graphically.
View SolutionA manufacturer makes two types of tea cups, say A and B. Three machines are needed for the manufacturing and the time in minutes required for each cup on the machine is given below:

Each machine is available for a maximum of 6 hrs per day. If the profit on each cup A is 75 paise and that on each cup B is 50 paise. If x and y denote the number of cups of ttpe A and B produced in a day respectively. What is the profit function ?
View SolutionA man owns a field of area `1,000` sq.m. He wants to plant fruit trees in it. He has a sum of Rs. `1,400` to purchase young trees. He has the choice of two types of the tree. Type `A` requires `10` sq.m of ground per tree and cost. Rs.`20` per tree and type `B` requires `20` sq.m of ground per tree and cost Rs. `25` per tree. When fully grown, type `A` produces an average of `20` kg fruit Which can be sold at a profit of Rs. `2` per kg and type `B` produces. an average of `40` kg of fruit which can be sold at a profit.of Rs. `1.50` per kg. How many of each type should he plant to achieve maximum profit when the trees are fully grown? What is the maximum profit?
View SolutionA furniture dealer sells only tables and chairs.He has Rs.12,000 to invest and a space to store 90 pieces.A table costs him Rs.400 and a chair Rs.100. He can sell a table at a profit of Rs.75 and a chair at a profit of Rs.25. Assume that he can sell all the items.The dealer wants to get maximum profit.By defining suitable variables ,write the objective function.
View Solution
QUESTION BANK questions and complete solutions for chapter LINEAR PROGRAMMING of V PUBLICATION of Class 12