Complete Solutions to Section -C (Long Answer Type Questions) of chapter MODEL PAPER 5 of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | MODEL PAPER 5 |
| VGS PUBLICATION-BRILLIANT | Section -C (Long Answer Type Questions) |
| Number Of Questions | 9 |
| Academic Year | 2023-24 |
If ` alpha, beta` are the roots of the equation ` x^(2) - 2x + 4 = 0 ` then for any`n in N` show that ` alpha^(n) + beta^(n) = 2^(n+1) cos ((n pi)/3)`.
05:27View SolutionSolve the `8x^3-36x^2-18x+81=0` equation, given that the roots of each are in A.P.
06:42View SolutionProve that : If n is a positive integer and x is any nonzero real number, then prove that
`C_(0)+C_(1)(x)/(2)+C_(2).(x^(2))/(3)+C_(3).(x^(3))/(4)+….+C_(n).(x^(n))/(n+1)=((1+x)^(n+1)-1)/((n+1)x)`06:15View SolutionIf `x=(1)/(5)+(1.3)/(5.10)+(1.3.5)/(5.10.15)+….oo` then find `3x^(2)+6x.`
04:03View SolutionFind the mean deviation about the median for the following continuous distribution:
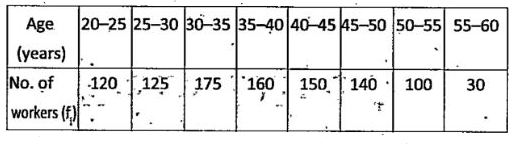 View Solution
View SolutionSuppose that an, urn `B_(1)` contains 2 white and.3 black balls and another urn `B_(2)` contains 3 white and 4 black balls. One urn is selected at random and a ball is drawn from it: If the ball drawn is found black, find the probability that the urn chosen was `B_(1).`
05:03View SolutionA random variable X has the following probability distribution.

Find k03:03View SolutionA random variable X has the following probability distribution.

Find (i) k (ii) Mean (iii) `P(0 lt X lt 5)`03:24View SolutionA random variable X has the following probability distribution:
`{:(X=x,P(X=x)),(0,0),(1,k),(2,2k),(3,2k),(4,3k),(5,k^2),(6,2k^2),(7,7k^2+k):}`
Find `p(0 lt x lt 5)`04:54View Solution
Section -C (Long Answer Type Questions) questions and complete solutions for chapter MODEL PAPER 5 of VGS PUBLICATION-BRILLIANT of Class 12
