Complete Solutions to Exercise-1 : Single Choice Problems of chapter COMPOUND ANGLES of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | COMPOUND ANGLES |
| VIKAS GUPTA | Exercise-1 : Single Choice Problems |
| Number Of Questions | 96 |
| Academic Year | 2023-24 |
`("cos"^(4)(pi)/(24)-"sin"^(4)(pi)/(24))` equals :
View SolutionIf `a sin x+b cos(c+x)+b cos(c-x)=alpha, alpha gt a`, then the minimum value of `|cos c|` is :
View SolutionIf all values of `x in (a, b)` satisfy the inequality `tan x tan 3x lt -1, x in (0, (pi)/(2))`, then the maximum value (b, -a) is :
View SolutionIf `A=pi/5,` then find the value of `sum_(r=1)^8tan(r A)tan((r+1)A)dot`
View SolutionLet `f(x)=2cos e c2x+secx+cos e cxdot` Then find the minimum value of `f(x)forx in (0,pi/2)dot`
View SolutionThe value of `"cosec"10^(@)+"cosec"50^(@)-"cosec"70^(@)` is _____
View SolutionIf `u=sqrt(a^2 cos^2 theta + b^2sin^2theta)+sqrt(a^2 sin^2 theta + b^2 cos^2 theta),` then the difference between the maximum and minimum values of `u^2` is given by : (a) `(a-b)^2` (b) `2sqrt(a^2+b^2)` (c) `(a+b)^2` (d) `2(a^2+b^2)`
View SolutionIf `u_n= sin (ntheta) sec^ntheta`, `v_n= cos(ntheta)sec^ntheta`, `n in N`, `n!=1`, then `(v_n-v_(n-1))/v_(n-1)+1/n(u_n/v_n)`=
View SolutionIf `a cos^ 3 3theta + b cos^4 theta = 16 cos^6 theta + 9 cos^2 theta` is an identity then-
View SolutionMaximum value of `cosx (sinx +cos x)` is equal to :
View SolutionIf `(sinA)/(sinB)=(sqrt(3))/(2) and (cosA)/(cosB)=(sqrt(5))/(2) , 0 lt A, B lt (pi)/(2)` then `tanA+tanB` is equal to :
View SolutionSingle Choice Questions: 1.Let `0<=alpha, beta, gamma, delta,<=pi` where `beta` and `gamma` are not complementary such that `2cos alpha+ 6 cos beta+7 cos gamma+9 cos delta=0` and `2 sin alpha- 6 sin beta+7 sin gamma-9 sin delta=0` if`cos(alpha+delta)/cos(beta+gamma)=m/n`when m and n are relatively prime positive numbers, then the value of `(m+n)` is equal to (A)11 (B)10 (C)9 (D)7
View SolutionIf `-pi lt theta lt -(pi)/(2)," then " |sqrt((1-sin theta)/(1+sintheta))+sqrt((1+sin theta)/(1-sin theta))|` is equal to :
View SolutionIf `A= sum _(r=1)^(3)"cos"(2r pi)/(7) and B=sum_(r=1)^(3)"cos"(2^(r )pi)/(7)`, then :
View SolutionIn a `Delta PQR` (as shown in figure) if `x:y:z=2:3:6`, then the value of `angle QPR` is :
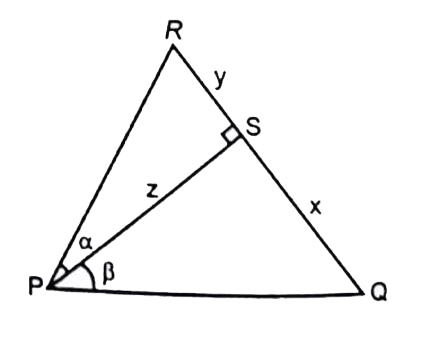
View SolutionIf `A= sum _(r=1)^(3)"cos"(2r pi)/(7) and B=sum_(r=1)^(3)"cos"(2^(r )pi)/(7)`, then :
View SolutionLet `f(x)=sinx+2cos^2x`, x `in [pi/6,(2pi)/3]`, then maximum value of f(x) is
View SolutionIn triangle `ABC, /_C = (2pi)/3` then the value of `cos^2 A + cos^2 B - cos A.cos B` is equal
View SolutionThe number of solutions of the equation `4sin^(2)x+tan^(2)x+cot^(2)x+"cosec"^(2)x=6" in " [0, 2pi]` :
View SolutionIf `sinA, cosA and tanA` are in G.P, the `cos^(3)A+cos^(2)A` is equal to :
View Solutionfind the range of function `f(x)=sin(x+(pi)/(6))+cos(x-(pi)/(6))`
View SolutionThe value of
`tan(log_(2)6)*tan(log_(2)3)*tan1` is always equal to :
View SolutionIn `DeltaABC, a = 3, b = 4` and `c = 5`, then value of `sinA + sin2B + sin3C` is
View SolutionIf `A+B+C=180^(@), " then " (cosAcosC+cos(A+B)cos(B+C))/(cosAsinC-sin(A+B)cos(B+C))` simplifies to :
View SolutionIf `alpha+gamma=2beta` then the expression `(sin alpha-sin gamma)/(cos gamma-cos alpha)` simplifies to:
View SolutionThe product `("cos"(x)/(2))*("cos"(x)/(4))*("cos"(x)/(8))* * * * * * * * ("cos"(x)/(256))` is equal to :
View SolutionThe value of the expression
`(sin7alpha+6sin 5 alpha+17sin3alpha+12sin alpha)/(sin6alpha+5sin 4alpha+12 sin 2 alpha)`, where `alpha=(pi)/(5)` is equal to :
View SolutionIn a triangle ABC if `sum tan^(2)A= sum tan A tan B`, then largest angle of the triangle in radian will be :
View SolutionWhich one of the following values is not the solution of the equation
`log_(|sin x|)(|cos x|)+log_(|cosx|)(|sin x|)=2`
View SolutionIf `f(x)=sin^6x+cos^6x ,` then range of `f(x)` is `[1/4,1]` (b) `[1/4,3/4]` (c) `[3/4,1]` (d) none of these
View SolutionIf `y=(2 sin alpha)/(1+cos alpha+sin alpha),"then"(1-cos alpha+sin alpha)/(1+sin alpha)` is equal to :
View SolutionIf `(tan^(3)A)/(1+tan^(2)A)+(cot^(3)A)/(1+cot^(2)A)=p secA"cosec"A+q sinA cosA`, then :
View SolutionIf `theta` lies in the second quadrant. Then the value of `sqrt((1-sin theta)/(1+sin theta))+sqrt((1+sin theta)/(1-sin theta))` is equal to :
View SolutionThe minimum value of `(sintheta+c o s e ctheta)^2+(costheta+sectheta)^2=`
View SolutionIf `log_(3) sin x-log_(3) cos x-log_(3)(1- tan x)-log_(3)(1+tan x)= -1`, then `tan2x` is equal to (wherever defined)
View SolutionIf `sin theta+ cosec theta =2,` then the value of `sin^8 theta + cosec^8 theta` is equal to
View SolutionIf `tan^(3)theta+cot^(3)theta=52`, then the value of `tan^(2)theta+cot^(2)theta` is equal to :
View SolutionThe maximum value of `(log)_(20)(3sin x-4cos x+15)-` a.`\ 1` b. `2` c. `3` d. `4`
View Solution`x^2 +y^2= 9 & 4a^2 + 9b^2= 16`, then maximum value of `4a^2 x^2+ 9b^2y^2- 12abxy` is -
View SolutionIf `A=sqrt(sin2-sin sqrt(3)), B=sqrt(cos2-cos sqrt(3))`, then which of the following statement is true ?
View SolutionThe number of real values of x such that
`(2^(x)+2^(-x)-2 cos x)(3^(x+pi)+3^(-x-pi)+2 cos x)(5^(pi-x)+5^(x-pi)-2 cos x)=0` is :
View SolutionShow that the equation `e^(sinx)-e^(-sinx)-4=0` has no real solution.
View SolutionIf `pi lt alpha lt (3pi)/(2)`, then find the value of expression `sqrt(4 sin^(4) alpha+sin^(2) 2 alpha) + 4 cos^(2)(pi/4 - alpha/2)`.
View Solution`(cos(pi/12)-sin(pi/12))(tan(pi/12)+cot(pi/12))=`
View Solution`tan(100^(@))+tan(125^(@))+tan(100^(@))tan(125^(@))=`
View SolutionIf `sin x+sin^(2)x=1, " then " cos^(8)x+2 cos^(6)x+cos^(4)x=`
View Solutionmaximum value of `log_5(3x+4y)` , if `x^2+y^2=25` is
View SolutionThe number of values of `theta` between `-pi and (3pi)/(2)` that satisfies the equation `5cos 2 theta+2 "cos"^(2)(theta)/(2)+1=0` is :
View SolutionGiven that `sin beta =(4)/(5), 0 lt beta lt pi and tan beta gt 0, " then " ((3 sin(alpha+beta)-4 cos (alpha+beta))"cosec"alpha` is equal to :
View SolutionThe maximum value of the function `f(x)=sin(x+pi/6)+cos(x+pi/6)` in the interval `(0,pi/2)` occurs at (a) `pi/(12)` (b) `pi/6` (c) `pi/4` (d) `pi/3`
View SolutionThe equation `sin x(sinx+cos x) = k` has real solutions, where k is a real number. Then
View SolutionThe value of `cos12^(@)cos24^(@)cos36^(@)cos48^(@)cos72^(@)cos84^(@),` is
View SolutionThe ratio of the maximum value to minimum value of `2cos^(2)theta+cos theta+1` is :
View SolutionIf all values of `x in (a, b)` satisfy the inequality `tan x tan 3x lt -1, x in (0, (pi)/(2))`, then the maximum value (b -a) is :
View SolutionThe area of a regular polygon of n sides is (where r is inradius, R is circumradius, and a is side of the triangle)
View SolutionFind the value of `cos 12^(@)+cos 84^(@)+cos 156^(@)+cos 132^(@)`
View Solution`(sin theta)/(cos(3theta))+(sin(3theta))/(cos(9theta))+(sin(9theta))/(cos(27theta))+(sin(27theta))/(cos(81theta))=`
View SolutionThe value of `("sin"(pi)/(9))(4+"sec"(pi)/(9))` is :
View SolutionIf `(dy)/(dx)=sin((x pi)/(2))cos(x pi)`, then y is strictly increasing in :
View SolutionSmallest positive value of `theta` satisfying `8sinthetacos2thetasin3thetacos4theta=cos6theta` is
View SolutionIf an angle A of a triangle ABC is given by `3 tanA+1=0`, then sinA and cosA are the roots of the equation
View SolutionIf `theta` is an acute angle and `t a ntheta=1/(sqrt(7))` , then the value of `(cos e c^2theta-sec^2theta)/(cos e c^2theta+sec^2theta)` is a. `3//4` b. `1//2` c. `2` d. `5//4`
View SolutionIf `2 cos theta + sin theta =1 then `7 cos theta + 6 sin theta` is equal to
View SolutionIf `sin theta+"cosec"theta=2`, then the value of `sin^(8)theta+"cosec"^(8) theta` is equal to :
View SolutionIf `tan^(3)theta+cot^(3)theta=52`, then the value of ` tan^(2)theta+cot^(2)theta` is equal to :
View SolutionIf ABCD is a cyclic quadrilateral such that `12tanA-5=0` and `5cosB+3=0` then `tanC+tanD` is equal to :
View SolutionIf `(pi)/(2) lt theta lt (3pi)/(2)` then `sqrt(tan^(2)theta-sin^(2)theta)` is equal to :
View SolutionThe value of `(sin10^(@)+sin20^(@))/(cos10^(@)+cos20^(@))` equals
View SolutionThe value of the expression `sin^6 theta + cos^6 theta + 3 sin^2 theta. cos^2 theta` equals
View Solution`(sinx+cosx)/(sinx-cos x)-(sec^(2)x+2)/(tan^(2)x-1)=`, where `x in (0, (pi)/(2))`
View SolutionIf `(cot alpha+cot(270^(@)+alpha))/(cot alpha-cot(270^(@)+alpha))-2 cos(135^(@)+alpha)cos(315^(@)-alpha)=lambda`, where `alpha in (0, (pi)/(2))`, then `lambda=`
View SolutionThe expression `(sin alpha+cos alpha)/(cos alpha-sin alpha) tan((pi)/(4)+alpha)+1, alpha in (-(pi)/(4), (pi)/(4))` simplifies to :
View SolutionThe value of expression `(tan alpha+sin alpha)/(2"cos"^(2)(alpha)/(2))` for `alpha=(pi)/(4)` is :
View Solution`cos2 alpha-cos3alpha-cos4alpha+cos5alpha` simplifies to :
View SolutionIf `tangamma=secalpha secbeta+tanalphatanbeta, then cos2 gamma` is necessarily
View SolutionIf `cosecx=2/sqrt3` and `cotx=-1/sqrt3` for x `in[0,2pi]` then `cosx+cos2x+cos3x+....+cos100x` is
View SolutionThe value of `sum_(r=0)^(10)cos^3(rpi)/3` is equal to `1/4` (b) `1/8` (c) `-1/4` (d) `-1/8`
View Solutionabout to only mathematics
View SolutionIf x,y `in`R and satisfy `(x+5)^2+(y-12)^2=14^2` then the minimum value of `x^2+y^2` is
View SolutionIf `theta_(1),theta_(2),theta_(3)` are three values lying in `[0,3pi)` for which `tan theta = lambda`, then the value of `|tan((theta_(1))/(3))tan((theta_(2))/(3))+tan((theta_(2))/(3))tan((theta_(2))/(3))+tan((theta_(3))/(3))tan((theta_(1))/(3))|` is
View SolutionIf `tan alpha =(b)/(a), a gt b gt 0 and " if " 0 lt alpha lt (pi)/(4), " then " sqrt((a+b)/(a-b))+sqrt((a-b)/(a+b))` is equal to :
View SolutionMinimum value of `3 sin theta+4 cos theta` in the interval `[0, (pi)/(2)]` is :
View SolutionIf `f(n)=prod_(r=1)^(n)cos r,n in N`, then
View SolutionIf `tantheta+sintheta=mandtantheta-sintheta=n`,then
View SolutionLet `t_(1)=(sin alpha)^(cos alpha), t_(2)=(sin alpha)^(sin alpha), t_(3)=(cosalpha)^(cos alpha), t_(4)=(cosalpha)^(sin alpha)`, where `alpha in (0, (pi)/(4))`, then which of the following is correct
View SolutionIf cosA=3/4, then 32 sin (A/2) sin ((5A) /2)= ------------- (A) √11 (B) -√11 (C) 11 (D) -11
View Solution`cos(alpha+beta)+sin(alpha-beta)=0"and"tanbeta=1/2009` ,find tan(alpha)
View SolutionIf `2^x=3^y=6^(-z)` find the value of `(1/x+1/y+1/z)`
View SolutionLet `alpha and beta` be such that `pi`<`alpha-beta<3pi,` If `sinalpha+sinbeta=-(21)/(65)` and `cosalpha+cosbeta=-(27)/(65)` , then the value of `cos(alpha-beta)/2 is` (a) `-3/(sqrt(130))` (b) `3/(sqrt(130))` (c) `6/(25)` (d) `6/(65)`
View SolutionIf `u=sqrt(a^2 cos^2 theta + b^2sin^2theta)+sqrt(a^2 sin^2 theta + b^2 cos^2 theta),` then the difference between the maximum and minimum values of `u^2` is given by : (a) `(a-b)^2` (b) `2sqrt(a^2+b^2)` (c) `(a+b)^2` (d) `2(a^2+b^2)`
View SolutionIf `P=(tan(3^(n+1)theta)-tan theta) and Q=sum_(r=0)^(n) (sin(3^(r )theta))/(cos(3^(r+1)theta))`, then
View SolutionIf `270^@ < theta < 360^@`, then `sqrt(2 + sqrt(2 + 2 cos theta))` is equal to
View SolutionIf `y= (sinx+cosx)+(sin4x+cos4x)^(2)`, then :
View SolutionIf `cosx+cosy+cosz=sinx+siny+sinz=0" then "cos(x-y)=`
View SolutionThe value of `"cosec"10^(@)+"cosec"50^(@)-"cosec"70^(@)` is _____
View SolutionIf `270^(@) lt theta lt 360^(@)`, then find `sqrt(2+sqrt(2(1+cos theta)))`
View Solution
Exercise-1 : Single Choice Problems questions and complete solutions for chapter COMPOUND ANGLES of SHRI BALAJI MATHS (ENGLISH) of Class 12