Complete Solutions to EXERCISE of chapter SAMPLE PAPER 09 of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | SAMPLE PAPER 09 |
| VIRAJ PUBLICATION | EXERCISE |
| Number Of Questions | 68 |
| Academic Year | 2023-24 |
`f : R to Z`, `f (x) = [x]` એ ...................
View Solutionજો `f : Q to R`, `f(x) = (2x-1)/(2)` અને `g : Q to R`, `g (x)=x+2` આપેલ વિધેય હોય, તો `(gof) ((3)/(2))` = ………………...
View Solutionજો `Q` પર `a` * `b = a+b - ab`, હોય તો * માટે અનુક્રમે તટસ્થ ઘટક ........ તથા `a` નો વ્યસ્ત ......... છે.
View Solution`cos (3 cos^(-1) ((1)/(3)))` = ………………
View Solution`sin^(-1) [cot (sin^(-1) (sqrt ((2-sqrt3)/(4))) + cos^(-1) ((sqrt12)/(4)) + sec^(-1) sqrt2)]` = …………….
View Solutionજો `cos^(-1) ((4)/(5)) + cosec^(-1) ((5)/(3) )= cot^(-1) k` હોય તો `k `= …………
View Solution`sin (cot^(-1)(1+x)) = cos (tan^(-1)x)` હોય, તો `x = ……….`
View Solution`A = [(0,0,1),(0,1,0),(1,0,0)]` માટે ........... સત્ય વિધાન છે.
View Solution`A = [(i,0),(0,i)]`, `B = [(o,i),(i,0)]`, જ્યાં `i = sqrt(-1)`, તો .....................
View Solution`A = [(cos alpha,sin alpha),(-sin alpha, cos alpha)]` તો `A^(-1)` = ………………..
View Solutionજો `A = [(3,3,3),(3,3,3),(3,3,3)]` તો `A^(3) = …………………. .`
View Solutionજો `|(1,2,5),(1,x,5),(3,-1,2)|=0` તો `x = ………………….. .`
View Solution`(2,5)`, `(7,k)` અને `(3,1)` શિરોબિંદુવાળા ત્રિકોણનું ક્ષેત્રફળ 10 હોય તો k નું મૂલ્ય ................
View Solutionજો `[(a,b,ax+by),(b,c,bx+cy),(ax+by,bx+cy,0)] = 0` અને `ax^(2) + 2bxy + cy^(2) ne 0` તો ……………. .
View Solution`[(d)/(dx) sec^(-1)x] _(x = -3)` = ………………….
View Solution`(d)/(dx) cdot ((1)/(log|x|))` ………………
View Solution`f(x) = {(3x+1),(kx-26),(x^(2)+a):}` `{:(, x lt= 3),(, 3 lt xlt5),(, x ge5):}` સતત વિધેય હોય, તો k = ………………… અને a = ……………… .
View Solution`f(x) = x + (1)/(x)`, `x ne 0` નું સ્થાનીય મહત્તમ મૂલ્ય ................ છે.
View Solutionનીયેના બહુવિકલ્પ પ્રશ્નોના જવાબ માટે સાયો વિકલ્પ પસંદ કરો
વફ `3x^(2) -y^(2)=8` પરના કિધું (2, -2) આગળના સ્પર્શનું સમીફરણ .........છે
View Solution`log_(e) 5.1` નું આસન્નમૂલ્ય ........... છે. `(log_(e)5=1.609)`
View Solution`f(x) = xe^(1-x)`, `x in R` એ ................... અંતરાલ પર ચુસ્ત વધતું વિધેય છે.
View Solution`int (dx)/(x^(4)-1)` …………. + c
View Solution`int (2^(x)+3^(x))/(4^(x)) dx = ……………. + c`
View Solution`int (dx)/(x^(2) sqrt(1-x^(2))) = ……………….. + c`
View Solution`int e^(cot^(-1)x)/(1 + x^(2)) (1-x+x^(2))` `dx` = ……………… + c
View Solution`int_((1)/(3))^(1) ((x-x^(3))^((1)/(3)))/(x^(4)) dx`
View Solution`int_(1)^(2) x |x| dx` = …………………. .
View Solution`int_(0)^((pi)/(2)) (cosx-sinx)/(1+cosxsinx) dx` = ……………………
View Solution`int_(1)^(e^(37)) (pi sin(pi log x))/(x) dx` = ……………….
View Solutionરેખાઓ `y=1-|x|` અને X-અક્ષ વડે આવૃત્ત પ્રદેશનું ક્ષેત્રફળ ............ છે.
View Solutionપરવલય `y^(2) = 4 ax` અને તેના નાભિલંબ વડે આવૃત્ત પ્રદેશનું ક્ષેત્રફળ ...................... છે.
View Solutionવક્ર `y=3 cos x`, `0 le x le (pi)/(2)` અને X-અક્ષ વડે આવૃત્ત પ્રદેશનું ક્ષેત્રફળ.... છે.
View Solutionવિકલ સમીકરણ `(1-y^(2)) (dx)/(dy) + yx = ay (-1 lt y lt 1)` નો સંકલ્યકારક અવયવ .......... છે.
View Solutionવિકલ સમીકરણ `((d^(2)y)/(dx^(2)))^(2) + 3 ((dy)/(dx))^(3) + 4 = 0` ની કક્ષા અને પરિમાણ અનુક્રમે .............. છે.
View Solution`y=ax^(3)` નું વિકલ સમીકરણ .............. છે. (a સ્વૈર અચળ)
View Solutionનીયેના બહુવિકલ્પ પ્રશ્નોના જવાબ માટે સાયો વિકલ્પ પસંદ કરો
`vec i.(vec j times vec k) +vec j.(vec i times vec k) +vec k.(vec i times vec j)` નું મૂલ્ચ .........થશે.
View Solutionજો `veca = hati + hatj + hatk`, `vecb = 4hati - 2 hatj + 3 hatk` `vecc = hati - 2 hatj + hatk`, `2 veca - vecb + 3 vecc` ની દિશામાંનો 6 માનવાળો સદિશ .................... .
View Solution`hati - 3 hatj - 4 hatk` અને `3 hati + hatj - 2 hatk` જેના વિકર્ણો હોય તેવા સમાંતરબાજુ ચતુષ્કોણનું ક્ષેત્રફળ ....................... થાય.
View Solution`lambda` = ……………. માટે `veca = hati+hatj+hatk`, `vecb=2 hati - 4 hatk` અને `vecc = hati + lambda hatj + 3 hatk`, સમતલીય બને.
View Solutionજો `vec a = hati+2hatj-3hatk`, અને `vecb=3hati-hatj+2hatk` હોય, તો સદિશો `veca+vecb` અને `veca-vecb` વચ્ચેના ખૂણાનું માપ ................... છે.
View Solutionસદિશ `veca = 2hati+3hatj-2hatk` ના સદિશ `vecb = hati+2hatj+3hatk` પરનો પ્રક્ષેપ = …………..
View Solutionઊગમબિંદુમાંથી સમતલ પરનો લંબપાદ `(a,b,c)` હોય, તો સમતલનું સમીકરણ ................... થાય.
View Solutionજો રેખાઓ `(x-1)/(c) = (y+2)/(-2) = (z-3)/(4)` અને `(x-5)/(1)=(y-3)/(1)=(z+1)/(c)` ની દિશાઓ સમાન હોય તો c = ……………..
View Solutionરેખા `(x+1)/(3k)=(y+3)/(2)=(z-4)/(5)` અને સમતલ `2x-3y-4z=12` સમાંતર હોય, તો k શોધો.
View Solutionસુરેખ આયોજનના પ્રશ્નનો શક્ય ઉકેલ ............. .
View Solutionજો સીમિત શક્ય ઉકેલના પ્રદેશના શિરોબિંદુઓનો યામ `(0, 0)`, `(2, 0)`, `(4, 2)`, `(2, 4)` અને `(0, (10)/(3))` હોય, તો હેતુલક્ષી વિધેય `z=-x+2y` માટે
(i) z ની મહત્તમ કિંમત ................ શિરોબિંદુએ મળે છે.
(ii) z ની ન્યૂનતમ કિંમત .............. શિરોબિંદુએ મળે છે.
(iii) z ની મહત્તમ કિંમત .............. છે.
(iv) z ની ન્યૂનતમ કિંમત ............. છે.
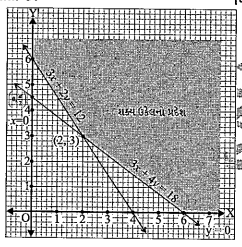
View Solutionઆકૃતિમાં દર્શાવ્યા પ્રમાણેના શક્ય ઉકેલના પ્રદેશની મર્યાદાઓ ........... છે.
View SolutionA સત્ય બોલે છે તેની સંભાવના `(4)/(5)` છે. એક સિક્કો ઉછાલ્યો છે. A માહિતી આપે છે કે છાપ મળી છે. ખરેખર છાપ હતી તેની સંભાવના .............. હોય.
View Solutionએક યાદૃચ્છિક ચલ X નું સંભાવના વિતરણ નીચે મુજબ છે :
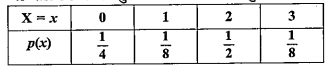 `E(2X+3)` ની કિંમત છે.
`E(2X+3)` ની કિંમત છે.
View Solutionએક નાના શહેરમાં એક અગ્નિશામક તથા એક ઍમ્બ્યુલન્સ છે. જ્યારે જરૂર પડે ત્યારે અગ્નિશામક હાજર હોય તેની સંભાવના `0.98` છે. અને ઍમ્બ્યુલન્સ હાજર હોય તેની સંભાવના `0.92` છે. જ્યારે ઇમારતમાં આગ લાગે ત્યારે અગ્નિશામક તથા ઍમ્બ્યુલન્સ એ બંને હાજર હોય તેની સંભાવના .............. છે.
View Solutionસાબિત કરો : `tan^(-1) ((1)/(5))+tan^(-1) ((1)/(7))+tan^(-1) ((1)/(3))+tan^(-1) ((1)/(8)) = (pi)/(4)`
View Solutionવિધેય `(cos x)^(y) = (cos y)^(x)` માટે `(dy)/(dx)` શોધો.
View Solution`(1)/(cos(x-a)cos(x-b))` વિધેયનું સંકલિત મેળવો.
View Solutionવક્ર `x^(2) = 4y`, Y-અક્ષ અને રેખાઓ `y=2` અને `y=4` દ્વારા આવૃત્ત પ્રથમ ચરણમાં આવેલ પ્રદેશનું ક્ષેત્રફળ શોધો.
View Solutionવર્તુળ `x^(2)+y^(2)=a^(2)` વડે આવૃત્ત પ્રદેશનું ક્ષેત્રફળ શોધો.
View Solutionસાબિત કરો કે `[veca +vecb, vecb+vecc, vecc+veca]=2[veca,vecb,vecc].`
View Solutionરેખાઓ `(1-x)/(3) = (7y-14)/(2p)=(z-3)/(2)` અને `(7-7x)/(3p)=(y-5)/(1)=(6-z)/(5)` પરસ્પર લંબ હોય, તો p નું મૂલ્ય શોધો.
View Solutionજેની ઉપર પૂર્ણાંકો 1,2,3 લાલ રંગથી અને 4,5,6 લીલા રંગથી લખેલ હોય તેવા પાસાને ફેંકવામાં આવે છે. પાસા પર મળતો પૂર્ણાંક યુગ્મ છે તે ઘટનાને A વડે તથા પાસા પરનો પૂર્ણાંક લાલ રંગથી લખેલ છે. તે ઘટનાને B વડે દર્શાવીએ, તો ઘટનાઓ A અને B નિરપેક્ષ છે?
View Solution`A = R-{3}` અને `B=R-{1}` છે. `f(x)= ((x-2)/(x-3))` દ્વારા વ્યાખ્યાયિત વિધેય `f: A to B` નો વિચાર કરો. શું f એક-એક અને વ્યાપ્ત છે? તમારા જવાબનું સમર્થન કરો.
View Solutionસમતોલ પાસાને ઉછાળતાં તેના પર મળતી સંખ્યાનું વિચરણ શોધો.
View Solution`y=sec^(-1)((1)/(2x^(2)-1))`, `0ltxlt(1)/(sqrt2)` તો `(dy)/(dx)` શોધો.
View Solution`(1,2,3)` માંથી પસાર થતી અને સમતલો `vecr cdot (hati-hatj+2hatk)=5` તથા `vecr cdot (3hati+hatj+hatk)=6` ને સમાંતર રેખાનું સદિશ સમીકરણ શોધો.
View Solutionઆપેલા સમતલ સમાંતર છે કે પરસ્પર લંબ છે તે નક્કી કરો અને જો આ પૈકી એક પણ ન હોય, તો તેમની વચ્ચેનો ખૂણો શોધો. `7x+5y+6z+30=0` અને `3x-y-10z+4=0`
View Solutionનીયોના આપેલા પ્રશ્ર્ન નંબર 9 થી 1 ની માગ્યા મુજખ ગણતરી કરી જવાખ આપો ( દરેકના 3 ગુણ છે.)
જો એક સમતોલ સિક્કાને 10 વાર ઉછાળવામાં આવે , તો
(a) બરાબર છ વખત છાપ મળે
(b) ઓછામાં ઓછી છ વખત છાપ મળે
(c) વઘુમા વઘુ છ વખત છાપ મળે તેની સંભાવના શોધો.
View SolutionFor the matrix `A=[{:(1,1,1),(1,2,-3),(2,-1,3):}]` Show that `A^3-6A^2+5A+11I=O`. Hence find `A^(-1)`
View Solutionવિધેય `f(x)=cos^(2)x+sin x, x in [0, pi]` નાં વૈશ્વિક મહત્તમ તથા વૈશ્વિક ન્યૂનતમ મૂલ્યો શોધો.
View Solution`overset((pi)/(4))underset(-(pi)/(4))int log (sin x+cosx)dx`
View Solutionવિકલ સમીકરણ `(dy)/(dx)+(y^(2)+y+1)/(x^(2)+x+1)=0` નો વ્યાપક ઉકેલ `(x+y+1)=A (1-x-y-2xy)` છે. તેમ દર્શાવો.
View Solution
EXERCISE questions and complete solutions for chapter SAMPLE PAPER 09 of VIRAJ PUBLICATION of Class 12