Complete Solutions to SUBJECTIVE PROBLEMS of chapter CHEMICAL BONDING (ADVANCED) of Class 12 book with complete answers and questions
| Class 12 | CHEMISTRY |
| Chapter | CHEMICAL BONDING (ADVANCED) |
| VK JAISWAL | SUBJECTIVE PROBLEMS |
| Number Of Questions | 72 |
| Academic Year | 2023-24 |
There are two groups of compounds A and B. Groups A contains three compounds `Px_(4), Qy_(3), Rz_(2)`. Groups B also contains three compounds `Sx_(4), Ty_(3), Uz_(2)`. Hybridization of each central atom of group A compounds is same as that of iodine in `IBrCl^(-)` while in group B compounds it is same as that of iodine `IBrCl^(+)`. Substituents X, Y and Z exhibit covalency of one in ground state. Then find the value of x/y.
Where, x and y are total number of lone pair present at central atoms of compounds of group A and B respectively.
View SolutionConsider the following three compounds `(i)AX_(2n)^(n-)`, (ii)`AX_(3n)` and (ii)`AX_(4n)^(n+)`, where central atom A is 15th group element and their maximum covalency is 3n. If total number of proton in surrounding atom X is n and value of n is one, then calculate value of `x^(3)+y^(2)+z^(2)` . (where x, y and z are total number of lone pair at central atom in compounds (i), (ii) and (iii) respectively.
View SolutionCondsider the following combination of atomic orbitals :
combinding orbitals (internuclear axis ) Combindig orbitals (internuclear axis).
(i) `s+p_(x)(x)` (ii)`d_(xy)+d_(xy)(x)` (iii)`d_(xy)+P_(x)(z)` (iv)`s+s(z)` (v)`d_(yz)+d_(yz)(x)` (vi)`p_(x)+p_(x)(z)` (vii)`d_(z^(2))+d_(z^(2))(z)` (viii)`d_(xy)+d_(xy)(z)` (ix)`p_(x)+p_(x)(y)` (x)`s+p_(z)(x)`
Then calculate value of `a^(2)+b^(2)+2cd`. (where `a=sigma M.O.,b=pi M.O. , C=delta M.O., `d=non-bonding M.O.)
View SolutionConsider the following six changes
(i)`NO to NO^(+)` (ii)`O_(2)^(-) to O_(2)^(2-)` (iii) `O_(2) to O_(2)^(+)` (iv)`NO^(+) to NO^(-)` (v) `NO^(+) to NO^(2+)` (vi) `CO to CO^(+)`
Then calculate value of `"c^(2)-b^(2)-a^(2)`", where a, b and c are total number of transformation in which magnetic property will be changed, bond order increase and bond order decrease respectively.
View SolutionWhen `B_(2)H_(4)` is allowed to react with following lewis bases, then how many given lewis bases form adduct through symmetrical cleavage of `B_(2)H_6)`?
`NH_(3), MeNH_(3)`, pyridine, CO, T.H.F., `PH_(3), PF_(3), Me_(3)N, Me_(3)NH`
View SolutionConsider the following elements A, B, C and D and their outer electronic configurtions are `ns^(2)np^(1), ns^(2)np^(3), ns^(2)np^(4) and ns^(2)np^(5)` respectively. Element E also has same outer electronic configuration like D but shows only single oxidation state(-1). If element A, B , C and D belong to same period as that of sodium. Consider the following compounds.
(i)`CE_(4)` (ii)`BD_(2)E_(3)` (iii)`DE_(3)` (iv)`DE_(2)` (v)`BD_(3)E_(2)` (vi)`C_(2)E_(2)` (vii)`DE` (viii)`A_(2)D_(6)`.
Then calculate the value of `"x+y"`, (where x and y are total number of polar and non-polar compounds).
View SolutionConsider following four compounds:
(i) `C_(x) O_(y)`
(ii) `C_(x)O_(y+1)`
(iii) `C_(x+2)O_(y+1)` and (iv) `C_(x+11)O_(y+8)`,
if "x=y=1", then calculate the vlaue of |p-q|, where p and q are total number of `sp^(2)` and hybridized carbon atoms respectively in given four compounds.
View SolutionTotal number of species among following which can use any one `t_(2g)` d-orbital in back bondin. `H_(4)SiO_(4), H_(2)NBF_(2), O(SiH_(3))_(2), CCl_(2), N(SiH_(3))_(2), (NB)_(x), R_(3)PO, P_(4)O_(10), CCl_(3)^(-)`
View SolutionCalculate expression `(x+y+z)` for diatomic molecules.
where x=Total number of singly occupied molecular orbital (SOMO) in `O_(2)`.
y=Total number of singly occupied molecular orbital (SOMO) in `B_(2)`
z=Total number of singly occupied molecular orbital (SOMO) in `NO`.
View SolutionIf Hund rule violate, then find the total number of species among following which whill be dimagnetic:
`B_(2), O_(2), N_(2)^(-), C_(2), NO, OF, N_(2)^(2-), BN`
View SolutionConsider the following table

Than calculate value of experssion `|(n_(1)+n_(2)+n_(3)+n_(4))/(m_(1)+m_(2)+m_(3)+m_(4))|^(2)`.
View SolutionTotal number of species among following, in which bond angle is equal to or less than `109^(@)28'` and also they act as lewis base :
`NH_(3), NMe_(3), O(SiH_(3))_(2), ICl_(4)^(-), XeO_(3), BF_(2)Cl, SiF_(4), AsH_(3), SO_(2)F_(2)`
View SolutionTotal number of unpaired electrons(s) present in both cationic and anionic part of compound `O_(2)[PtF_(6)]`.
View SolutionTotal number of species which has/ have symmetrical electronic distribution in their HOMO and also paramagnetic.
`N_(2)^(+), O_(2)^(2-), C_(2), O_(2), B_(2), C_(2)^(2-), N_(2)^(2-)`.
View SolutionTotal number of molecules, in which each covalent bond is comprised of effective back bond. `BF_(3), N(SiH_(3))_(3), PF_(3),, POF_(3), B(OH)_(3), O(SiH_(3))_(2), BFH_(2), BF_(2)(NH_(2)), NH(SiH_(3))_(2)`
View SolutionTotal number of angle in `SeCl_(4)` which are less than `90^(@)`.
View SolutionConsider the following species `O(Me)_(2), N(SiH_(3))_(3), CO, O(SiH_(3))_(2), CCl_(2)("singlet"), CCl_(3)^(-), H_(4)SiO_(4), OCl_(2), MeNCS`. Then calculate the number of species which have `(p_(pi)-p_(x))` back bond or `(p_(pi)-d_(pi)` back bond.
View SolutionTotal number of molecules which can form H-bond among themselves.
`SiH_(3)OH, HCN, B(OM e)_(3), NHM e_(2), CH_(3)CONH_(2), HCHO, HCOOH, NH_(2)OH, H_(4)SiO_(4)`
View SolutionConsider two covalent compounds `AL_(n_(1)) and BL_(n_(2))`, if central atom (A) of first compounds has total six electron pairs and central atom (B) of second compound contains total five electron pairs in its valence shell and both compounds are planar and non-polar then calculate value of experssion `(n_(1)-n_(2))^(2)`.
[Where `n_(1) and n_(2)` are number of monovalent surrounding atom (L)]
View SolutionCalculate the `I-I` distance in (Å) for given compound `H_(2)C_(2) I_(2)` if `C-I` bond length is 2.35Å. `(sin60^(@)=0.866)`
View SolutionThere are some arrangements of atomic orbitals which are given below:
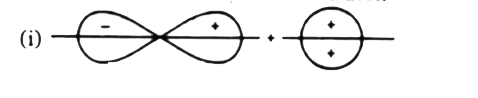
Then calculate the value of "`QtimesR-P'" where P, Q and R are no. of arrangements which give bonding molecular orbitals (positive overlap), antibonding molecular orbitals (negative overlap) and non-bonding molecular orbitals (zero overlap) respectively.
View SolutionNumber of hybrid orbital C atoms which have 33% p-character in `C(CN)_(4)`.
View SolutionMax. no. of equal `P-O` bonds in `P_(2)O_(7)^(4-)` ion is :
View SolutionConsider the following species:
(i) `CH_(3)^(+)`
(ii) `(C_(3)H_(5))_(3)Al`
(iii) `HCHO`
(iv) `CH_(4)`
(v) `(C_(2)H_(5))_(3)N`
(vI) `TiCl_(4)`
(vii) `CO_(2)`
(viii) `SiCl_(4)`
(ix) `BF_(3)`
the find out total number of species which can act as Lewis acid.
View SolutionCalculate value of |x-y|, here x and y are the total number of bonds in benzene and benzyne respectively which are formed by overlapping of hybridized orbitals.
View SolutionConsider the following compounds :
`(i) IF_(5) " " (ii) ClI_(4)^(-) " " (iii) XeO_(2)F_(2) " " (iv) NH_(2)^(-) `
`(v) BCl_(3) " " (vi) BeCl_(2) " " (vii) AsCl_(4)^(+) " " (viii) B(OH)_(3)`
(ix) `NO_(2)^(-) " " (x) ClO_(2)^(+)`
Then calculate value of "x+y-z", here, x,y and z are total number of compounds in given compounds in which central atom used their all three p-orbitals, only two p-orbitals and only one p-orbital in hybridisation respectively .
View SolutionConsider the following
Calculate value of `p+q`, here p and q are total number of `dpi-ppi` bonds and total number of `sp^(3)` hybridised atoms respectively in given molecule.
View SolutionConsider the following orbitals (i)`3p_(x)` (ii)`4d_(x^(2))` (iii)`3d_(x^(2)-y^(2))` (iv)`3d_(yz)`
Then, calculate value of "`x+y-z`" here x is total number of gerade orbital and y is total number of ungerade orbitals and z is total number of axial orbitals in given above orbitals.
View SolutionConsider the following oxyanions:
`PO_(4)^(3-),P_(2)O_(6)^(4-),SO_(4)^(2-),MnO_(4)^(-),CrO_(4)^(2-),S_(2)O_(5)^(2-),S_(2)O_(7)^(2-)`
and find the value of R+Q-P
where P-number of oxy anions having three equivalent X-O bonds per central atom
Q=number of oxy anions having two equivalent X-O bonds per central atom.
R=Number of oxy anions having four equivalent X-O bonds per central atom.
View SolutionConsider the following three compounds `(i)AX_(2n)^(n-)`, (ii)`AX_(3n)` and (ii)`AX_(4n)^(n+)`, where central atom A is 15th group element and their maximum covalency is 3n. If total number of proton in surrounding atom X is n and value of n is one, then calculate value of `x^(3)+y^(2)+z^(2)` . (where x, y and z are total number of lone pair at central atom in compounds (i), (ii) and (iii) respectively.
View SolutionConsider the following compounds and Calculate the value of `((P^(2)-Q^(2))/(R+S))`
(i)`BeF` (ii)`ICl` (iii)`BeF_(3)` (iv)`BrF_(5)` (v)`ICl_(3)` (vi)`IF_(3)` (vii)`IF_(5)` (viii)`IF_(7)`,
Where P: Total number of polar compounds.
Q: Total number of planar compounds.
R: Total number of non-polar compounds.
S: Total number of non-planar compounds.
View SolutionConsider the following compounds
(1)`H_(3)CF` (2)`H_(2)CF_(2)` (3)` CH_(4)` (4)`H_(3)C CF_(3)` (5)`CH_(3)CH_(3)` (6)`C_(2)H_(4)`
and calculate value of Y+X, (where X is the total number of compounds which have `H-C-H` bond angles equal to `109^(@)28'` and Y is the total number of compounds which have `H-C-H` bond angles greater than `109^(@)28'` and less than `120^(@)`
View SolutionThere are some species given below :-
`{:((a)O_(2)^(+),,,,(b)CO),((c)B_(2),,,,(d)O_(2)^(+)),((e)NO^(+),,,,(f)He_(2)^(+)),((g)C_(2)^(+2),,,,(h)CN^(-)),((i)N_(2)^(-),,,,):}`
Total no. of species which have their fractional bond order.
View SolutionFollowing compounds A and B have similar structure with delocalization of `pi`-electrons system. `(A)(PNCl_(2))_("x/2")` (B)`(CH)_(x)`
If value of x is 6, then calculate value of "P+Q", where 'P' is total no. of `sigma`-bonds in compounds A and B and 'Q' is total no. of `pi` bonds in compounds A and B.
View SolutionThe hybridization of central atoms of compounds A, B, C and D are `sp^(3)d, sp^(3), sp^(2) and sp` respectively. If compounds A and D have same shape like `I_(3)^(-)` and compounds B and C have same shape like water structure. Then calculate value of "P+Q+R+S", where P, Q, R, and S are number of lone pairs on central atoms of compounds A, B, C and D respectively.
View SolutionIn compound `PCl_(x)F_(5-x)`, possible values of x are 0 to 5, then calculate value of `x_(1)+x_(2)+x_(3)` (where `x_(1), x_(2) and x_(3)`… are possible values of x, with zero dipole moment for given compound).
View SolutionThere are two groups of compounds A and B. Groups A contains three compounds `Px_(4), Qy_(3), Rz_(2)`. Groups B also contains three compounds `Sx_(4), Ty_(3), Uz_(2)`. Hybridization of each central atom of group A compounds is same as that of iodine in `IBrCl^(-)` while in group B compounds it is same as that of iodine `IBrCl^(+)`. Substituents X, Y and Z exhibit covalency of one in ground state. Then find the value of x/y.
Where, x and y are total number of lone pair present at central atoms of compounds of group A and B respectively.
View SolutionConsider the following three compounds `(i)AX_(2n)^(n-)`, (ii)`AX_(3n)` and (ii)`AX_(4n)^(n+)`, where central atom A is 15th group element and their maximum covalency is 3n. If total number of proton in surrounding atom X is n and value of n is one, then calculate value of `x^(3)+y^(2)+z^(2)` . (where x, y and z are total number of lone pair at central atom in compounds (i), (ii) and (iii) respectively.
View SolutionCondsider the following combination of atomic orbitals :
combinding orbitals (internuclear axis ) Combindig orbitals (internuclear axis).
(i) `s+p_(x)(x)` (ii)`d_(xy)+d_(xy)(x)` (iii)`d_(xy)+P_(x)(z)` (iv)`s+s(z)` (v)`d_(yz)+d_(yz)(x)` (vi)`p_(x)+p_(x)(z)` (vii)`d_(z^(2))+d_(z^(2))(z)` (viii)`d_(xy)+d_(xy)(z)` (ix)`p_(x)+p_(x)(y)` (x)`s+p_(z)(x)`
Then calculate value of `"a^(2)+b^(2)+2cs"`. (where `a=sigma M.O.,b=pi M.O. , C=delta M.O., `d=non-bonding M.O.)
View SolutionConsider the following sic changes
(i)`NO to NO^(+)` (ii)`O_(2)^(-) to O_(2)^(2-)` (iii) `O_(2) to O_(2)^(+)` (iv)`NO^(+) to NO^(-)` (v) `NO^(+) to NO^(2+)` (vi) `CO to CO^(+)`
Then calculate value of `"c^(2)-b^(2)-a^(2)`", where a, b and c are total number of transformation in which magnetic property will be changed, bond increase and bond order decrease respectively.
View SolutionWhen `B_(2)H_(4)` is allowed to react with following lewis bases, then how many given lewis bases form adduct through symmetrical cleavage of `B_(2)H_6)`?
`NH_(3), MeNH_(3)`, pyridine, CO, T.H.F., `PH_(3), PF_(3), Me_(3)N, Me_(3)NH`
View SolutionConsider the following elements A, B, C and D and their outer electronic configurtions are `ns^(2)np^(1), ns^(2)np^(3), ns^(2)np^(4) and ns^(2)np^(5)` respectively. Element E also has same outer electronic configuration like D but shows only single oxidation state(-1). If element A, B , C and D belong to same period as that of sodium. Consider the following compounds.
(i)`CE_(4)` (ii)`BD_(2)E_(3)` (iii)`DE_(3)` (iv)`DE_(2)` (v)`BD_(3)E_(2)` (vi)`C_(2)E_(2)` (vii)`DE` (viii)`A_(2)D_(6)`.
Then calculate the value of `"x+y"`, (where x and y are total number of polar and non-polar compounds).
View SolutionConsider following four compounds:
(i) `C_(x) O_(y)`
(ii) `C_(x)O_(y+1)`
(iii) `C_(x+2)O_(y+1)` and (iv) `C_(x+11)O_(y+8)`,
if "x=y=1", then calculate the vlaue of |p-q|, where p and q are total number of `sp^(2)` and hybridized carbon atoms respectively in given four compounds.
View SolutionTotal number of species among following which can use any one `t_(2g)` d-orbital in back bondin. `H_(4)SiO_(4), H_(2)NBF_(2), O(SiH_(3))_(2), CCl_(2), N(SiH_(3))_(2), (NB)_(x), R_(3)PO, P_(4)O_(10), CCl_(3)^(-)`
View SolutionCalculate expression `(x+y+z)` for diatomic molecules.
where x=Total number of singly occupied molecular orbital (SOMO) in `O_(2)`.
y=Total number of singly occupied molecular orbital (SOMO) in `B_(2)`
z=Total number of singly occupied molecular orbital (SOMO) in `NO`.
View SolutionIf Hund rule violate, then find the total number of species among following which whill be dimagnetic:
`B_(2), O_(2), N_(2)^(-), C_(2), NO, OF, N_(2)^(2-), BN`
View SolutionConsider the following table

Than calculate value of experssion `|(n_(1)+n_(2)+n_(3)+n_(4))/(m_(1)+m_(2)+m_(3)+m_(4))|^(2)`.
View SolutionTotal number of species among following, in which bond angle is equal to or less than `109^(@)28'` and also they act as lewis base :
`NH_(3), NMe_(3), O(SiH_(3))_(2), ICl_(4)^(-), XeO_(3), BF_(2)Cl, SiF_(4), AsH_(3), SO_(2)F_(2)`
View SolutionTotal number of unpaired electrons(s) present in both cationic and anionic part of compound `O_(2)[PtF_(6)]`.
View SolutionTotal number of species which has/ have symmetrical electronic distribution in their HOMO and also paramagnetic.
`N_(2)^(+), O_(2)^(2-), C_(2), O_(2), B_(2), C_(2)^(2-), N_(2)^(2-)`.
View SolutionTotal number of molecules, in which each covalent bond is comprised of effective back bond. `BF_(3), N(SiH_(3))_(3), PF_(3),, POF_(3), B(OH)_(3), O(SiH_(3))_(2), BFH_(2), BF_(2)(NH_(2)), NH(SiH_(3))_(2)`
View SolutionTotal number of angle in `SeCl_(4)` which are less than `90^(@)`.
View SolutionConsider the following species `O(Me)_(2), N(SiH_(3))_(3), CO, O(SiH_(3))_(2), CCl_(2)("singlet"), CCl_(3)^(-), H_(4)SiO_(4), OCl_(2), MeNCS`. Then calculate the number of species which have `(p_(pi)-p_(x))` back bond or `(p_(pi)-d_(pi)` back bond.
View SolutionTotal number of molecules which can form H-bond among themselves.
`SiH_(3)OH, HCN, B(OMe)_(3), NHMe_(2), CH_(2)CONH_(2), HCHO, HCOOH, NH_(2)OH, H_(4)SiO_(4)`
View SolutionConsider two covalent compounds `AL_(n_(1)) and BL_(n_(2))`, if central atom (A) of first compounds has total six electron pairs and central atom (B) of second compound contains total five electron pairs in its valence shell and both compounds are planar and non-polar then calculate value of experssion `(n_(1)-n_(2))^(2)`.
[Where `n_(1) and n_(2)` are number of monovalent surrounding atom (L)]
View SolutionCalculate the `I-I` distance in (Å) for given compound `H_(2)C_(2) I_(2)` if `C-I` bond length is 2.35Å. `(sin60^(@)=0.866)`
View SolutionThere are some arrangements of atomic orbitals which are given below:

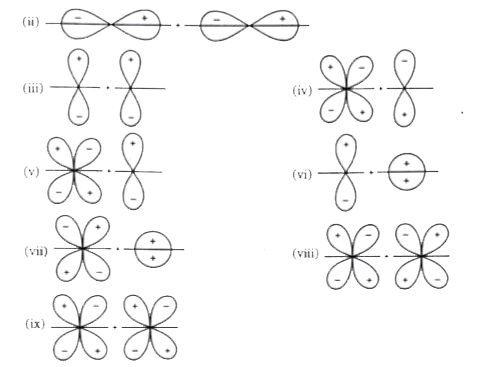 Then calculate the value of "`QtimesR-P'" where P, Q and R are no. of arrangements which give bonding molecular orbitals (positive overlap), antibonding molecular orbitals (negative overlap) and non-bonding molecular orbitals (zero overlap) respectively.
Then calculate the value of "`QtimesR-P'" where P, Q and R are no. of arrangements which give bonding molecular orbitals (positive overlap), antibonding molecular orbitals (negative overlap) and non-bonding molecular orbitals (zero overlap) respectively.
View SolutionNumber of hybrid orbital C atoms which have 33% p-character in `C(CN)_(4)`.
View SolutionMax. no. of equal `P-O` bonds in `P_(2)O_(7)^(4-)` ion is :
View SolutionConsider the following species:
(i) `CH_(3)^(+)`
(ii) `(C_(3)H_(5))_(3)Al`
(iii) `HCHO`
(iv) `CH_(4)`
(v) `(C_(2)H_(5))_(3)N`
(vI) `TiCl_(4)`
(vii) `CO_(2)`
(viii) `SiCl_(4)`
(ix) `BF_(3)`
the find out total number of species which can act as Lewis acid.
View SolutionCalculate value of `|x-y|`, here x and y are the total number of bonds in benzene and benyne respectively which are formed by overlapping of hybridized orbitals .
View SolutionConsider the following compounds :
`(i) IF_(5) " " (ii) ClI_(4)^(-) " " (iii) XeO_(2)F_(2) " " (iv) NH_(2)^(-) `
`(v) BCl_(3) " " (vi) BeCl_(2) " " (vii) AsCl_(4)^(+) " " (viii) B(OH)_(3)`
(ix) `NO_(2)^(-) " " (x) ClO_(2)^(+)`
Then calculate value of "x+y-z", here, x,y and z are total number of compounds in given compounds in which central atom used their all three p-orbitals, only two p-orbitals and only one p-orbital in hybridisation respectively .
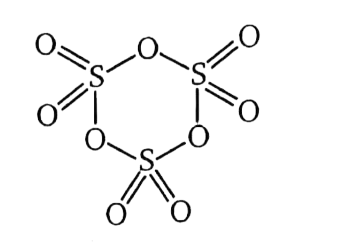
View SolutionConsider the following

Calculate value of `p+q`, here p and q are total number of `dpi-ppi` bonds and total number of `sp^(3)` hybridised atoms respectively in given molecule.
View SolutionConsider the following orbitals (i)`3p_(x)` (ii)`4d_(x^(2))` (iii)`3d_(x^(2)-y^(2))` (iv)`3d_(yz)`
Then, calculate value of "`x+y-z`" here x is total number of gerade orbital and y is total number of ungerade orbitals and z is total number of axial orbitals in given above orbitals.
View SolutionConsider the following oxyanions :
`PO_(4)^(3-), P_(2)O_(6)^(4-), SO_(4)^(2-), MnO_(4)^(-), CrO_(4)^(2-), S_(2)O_(5)^(2-), S_(2)O_(7)^(2-)` and find the value of `R+Q-P`
where
P=Number of oxy aions having three equivalent
`X-O` bonds per central atom
O=Number of oxy anions having two equivalent
`X-O` bonds per central atom
R=Number of oxy anions having four equivalent
`X-O` bonds per central atom
View SolutionConsider the following three compounds `(i)AX_(2n)^(n-)`, (ii)`AX_(3n)` and (ii)`AX_(4n)^(n+)`, where central atom A is 15th group element and their maximum covalency is 3n. If total number of proton in surrounding atom X is n and value of n is one, then calculate value of `x^(3)+y^(2)+z^(2)` . (where x, y and z are total number of lone pair at central atom in compounds (i), (ii) and (iii) respectively.
View SolutionConsider the following compounds and Calculate the value of `((P^(2)-Q^(2))/(R+S))`
(i)`BeF` (ii)`ICl` (iii)`BeF_(3)` (iv)`BrF_(5)` (v)`ICl_(3)` (vi)`IF_(3)` (vii)`IF_(5)` (viii)`IF_(7)`,
Where P: Total number of polar compounds.
Q: Total number of planar compounds.
R: Total number of non-polar compounds.
S: Total number of non-planar compounds.
View SolutionConsider the following compounds
(1)`H_(3)CF` (2)`H_(2)CF_(2)` (3)` CH_(4)` (4)`H_(3)C CF_(3)` (5)`CH_(3)CH_(3)` (6)`C_(2)H_(4)`
and calculate value of Y+X, (where X is the total number of compounds which have `H-C-H` bond angles equal to `109^(@)28'` and Y is the total number of compounds which have `H-C-H` bond angles greater than `109^(@)28'` and less than `120^(@)`
View SolutionThere are some species given below. (i)`O_(2)^(+)` (ii)`CO` (iii)`B_(2)` (iv)`O_(2)^(-)` (v)`NO^(+)` (vi)`He_(2)^(+)` (vii)`C_(2)^(2+)` (vii)` CN^(-)` (ix)` N_(2)^(-)`
total number of species which have fractional bond order.
View SolutionFollowing compounds A and B have similar structure with delocalization of `pi`-electrons system. `(A)(PNCl_(2))_("x/2")` (B)`(CH)_(x)`
If value of x is 6, then calculate value of "P+Q", where 'P' is total no. of `sigma`-bonds in compounds A and B and 'Q' is total no. of `pi` bonds in compounds A and B.
View SolutionThe hybridization of central atoms of compounds A, B, C and D are `sp^(3)d, sp^(3), sp^(2) and sp` respectively. If compounds A and D have same shape like `I_(3)^(-)` and compounds B and C have same shape like water structure. Then calculate value of "P+Q+R+S", where P, Q, R, and S are number of lone pairs on central atoms of compounds A, B, C and D respectively.
View SolutionIn compound `PCl_(x)F_(5-x)`, possible values of x are 0 to 5, then calculate value of `x_(1)+x_(2)+x_(3)` (where `x_(1), x_(2) and x_(3)`… are possible values of x, with zero dipole moment for given compound).
View Solution
SUBJECTIVE PROBLEMS questions and complete solutions for chapter CHEMICAL BONDING (ADVANCED) of VK JAISWAL CHEMISTRY (HINGLISH) of Class 12