Complete Solutions to EXERCISE (SINGLE CHOICE PROBLEMS) of chapter QUADRATIC EQUATIONS of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | QUADRATIC EQUATIONS |
| VK JAISWAL | EXERCISE (SINGLE CHOICE PROBLEMS) |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
Sum of values of `x` and `y` satisfying `3^x-4^y=77, 3^(x/2)-2^y=7` is
View SolutionIf `f(x) =Pi_(i=1)^3(x-a_i) + sum_(i=1)_3 a_i - 3x` where `a_i < a_(i+1)` for i = 1,2, then f(x) = 0 have
View SolutionComplete set of real values of 'a' for which the equation `x^4-2ax^2+x+a^2 -a=0` has all its roots real
View SolutionThe cubic polynomial with leading coefficient unity all whose roots are 3 units less than the roots of the equation `x ^(3) -3x ^(2) -4x +12=0` is denoted as `f (x) ` then `f '(x)` is equal to :
View SolutionThe set of value of `k (k in R)` for which the equation `x ^(2) -4 |x|+3 -|k-1|=0` will have exactly four real roots, is:
View SolutionThe number of integers satisfying the inequality is `x/(x+6)<=1/x`
View SolutionThe product of uncommon real roots of the polynomials ` p(x)=x^4+2x^3-8x^2-6x+15` and ` q(x) ` `= x^3+4x^2-x-10 ` is :
View SolutionIf `lamda_1, lamda_2 (lambda_1 > lambda_2)` are two values of `lambda` for which the expression `f(x,y) = x^2 + lambdaxy +y^2 - 5 x - 7y + 6` can be resolved as a product of two linear factors, then the value of `3lamda_1 + 2lamda_2` is
View SolutionLet `alpha,beta` be the roots of the quadratic equation `ax^2+bx+c=0` then the roots of the equation `a(x+1)^2+b(x+1)(x-2)+c(x-2)^2=0` are:-
View SolutionIf a,b `in` R distinct numbers satisfying |a-1| + |b-1| = |a| + |b| = |a+1| + |b+1|, Then the minimum value of |a-b| is :
View SolutionThe smallest positive integer p for which expression `x ^(2)- 2px +3p[+4` is negative for atleast one real x is:
View SolutionIf x `in` R then `(x^(2)+2x+a)/(x^(2)+4x+3a)` can take all real values if
View SolutionIf 2 lies between the roots of the equation `t ^(2) - mt +2 =0,(m in R)` then the value of `[((2 |x|)/(9+x ^(2)))^(m)]` is:
(where [.] denotes greatest integer function)
View SolutionThe number of integral roots of the equation `x ^(8) -24x ^(7) -18x ^(5) +39x ^(2) +1155=0` is:
View SolutionIf the value of `m^4+1/m^4=119` then the value of `|m^3-1/m^3|`=
View SolutionIf the equation `ax^2+2bx+c=0` and `ax^2+2cx+b=0`, `a!=o`, `b!=c`, have a common too then their other roots are the roots of the quadratic equation
View SolutionIf `cos alpha, cos beta and c gamma `are the roots of the equation `9x ^(3)-9x ^(2) -x+1 =0, alpha, beta , gamma in [0,pi]` then the radius of the circle whose centre is `(sum alpha, sum cos alpha)` and passing through `(2 sin ^(-1) (tan pi//4), 4)` is :
View SolutionFor real values of x, the value of expression `(11x^2-12x-6)/(x^2+4x+2)`
View Solution`(x+3)/(x ^(2)-2) ge (1)/(x-4)` holds for all x satisfying :
View SolutionIf `x=4+3i` (where `I =sqrt(-1)),` then the value of `x ^(3)-4x ^(2)-7x+12` equals:
View SolutionLet `f (x) =(x^(2) +x-1)/(x ^(2) x-1),` then the largest vlaue of `f (x) AA x in [-1, 3]` is:
View SolutionLet `f (x) =(x^(2) +x-1)/(x ^(2) - x+1)`, In above problem, the range of `f (x) AA x in [-1, 1]` is:
View SolutionIf the roots of the equation `1/(x+p) + 1/(x+q) = 1/r` are equal in magnitude but opposite in sign and its product is ` alpha `
View SolutionThe roots of `a_1x^2+b_1x + c_1=0`are reciprocal of the roots of the equation `a_2x^2 +b_2x+c_2=0` if
View SolutionIf `alpha!= beta` but `alpha^2 = 5alpha-3, beta^2 = 5beta - 3`, then find the equation whose roots are `alpha/beta and beta/alpha`.
View SolutionIf the difference between the roots of `x^2+ax+b=0` is same as that of `x^2+bx+a= 0` `a!=b`, then:
View SolutionIf `tan theta_1,tantheta_2,tan theta_3,tan theta_4` are the roots of the equation `x^4-x^3sin2beta+x^2cos2beta-xcosbeta-sinbeta=0` then prove that `tan(theta_1+theta_2+theta_3+theta_4)=cot beta `
View SolutionLet a,b,c , d ar positive real number such that `a/b ne c/d,` then the roots of the equation: `(a^(2) +b^(2)) x ^(2) +2x (ac+ bd) + (c^(2) +d^(2))=0` are :
View SolutionIf `alpha, beta` are the roots of `ax^2 + bx + c = 0,` the equation whose roots are `2 + alpha, 2 + beta` is
View SolutionMinimum posible number of positive root of the quadratic equation
`x ^(2) -(1+ lamda) x + lamda -2 =0, lamda in R: `
View SolutionLet `alpha, beta ` be ral roots of the quadratic equation`x ^(2)+kx+ (k^(2) +2k-4) =0,` then the minimum value of `alpha ^(z)+beta ^(z)` is equal to :
View SolutionPolynomial `P (x)=x ^(2)-ax +5 and Q(x)=2x ^(3)+5x-(a-3)` when divided by `x-2` have same remainders, then 'a' is equal to
View SolutionIf `a and b(!=0)` are the roots of the equation `x^2+ax+b=0` then the least value of `x^2+ax+b` is
View SolutionLet `alpha,beta` be the roots of the equation `ax^2+bx+c=0`. A root of the equation `a^3x^2+abcx+c^3=0` is (i) `alpha+beta` (ii) `alpha^2+beta` (iii)`alpha^2-beta` (iv) `alpha^2beta`
View SolutionLet a, b, c be the lengths of the sides of a triangle (no two of them are equal) and `k in R`.If the roots of the equation `x^2 + 2(a+b+c)x+6k(ab+bc+ac)=0` are real, then:
View SolutionRoot(s) of the equatio `9x^(2) - 18|x|+5 = 0` belonging to the domain of definition of the function `f(x) = log(x^(2) - x - 2)`, is (are)
View SolutionIf `beta + cos ^(2) alpha, beta + sin ^(2) alha ` are the roots of `x ^(2) + 2 bx +c=0 and gamma + cos ^(4) alpha, gamma + sin ^(4) alpha ` are the roots of `x ^(2) + 2Bx+C=0,` then :
View SolutionMinimum vlaue of `|x-p| + |x-15| +|x-p-15|.` If `p le x le 15 and 0 lt p lt 15` :
View SolutionIf the equadratic equation `4x ^(2) -2x -m =0 and 4p (q-r) x ^(2) -2p (r-p) x+r (p-q)-=0` have a common root such that second equation has equal roots then the vlaue of m will be :
View SolutionThe range of k for which the inequality `kcos^2x-kcosx+1>=0AAxepsilon(-oo,oo)` is:
View SolutionIf `(1+alpha)/(1-alpha),(1+beta)/(1-beta), (1+gamma)/(1-gamma)` are the cubic equation f(x) = 0 where `alpha,beta,gamma` are the roots of the cubic equation `3x^3 - 2x + 5 =0`, then the number of negative real roots of the equation f(x) = 0 is :
View SolutionThe sum of all intergral values of `lamda` for which `(lamda^(2) + lamda -2) x ^(2) + (lamda +2) x lt 1 AA x in R,` is:
View SolutionIf `alpha,beta,gamma,delta in R` satisfy `((alpha+1)^2+(beta+1)^2+(gamma+1)^2+(delta+1)^2)/(alpha+beta+gamma+delta) = 4` If biquadratic equation `a_0 x^4 + a_1 x^3 + a_2 x^2 + a_3 x _ a_4 =0` has the roots `(alpha+1/beta -1),(beta +1/gamma -1),(gamma+1/delta -1),(delta+1/alpha -1)`. then the value of `a_2/a_0` is
View SolutionIf the complete set of value of x satisfying `|x-1|+|x-2|+|x-3|>=6` is `(-oo,a]uu[b,oo)`, then `a+b=`
View SolutionIf exactly one root of the quadratic equation `x ^(2) -(a+1 ) +2a =0` lies in the interval `(0,3)` then the set of value 'a' is given by :
View SolutionThe condition that the roots of `x^3 +3 px^2 +3qx +r = 0` may be in `H.P.` is
View SolutionIf x is ral and `4y ^(2)+4 xy +x +6=0,` then the complete set of values of x for which y is real, is :
View SolutionThe solution of the equation `log _( cosx ^(2)) (3-2x) lt log _( cos x ^(2)) (2x -1) ` is:
View SolutionThe roots `alpha and beta` of the quadratic equation `px^(2) + qx + r = 0` are real and of opposite signs. The roots of `alpha(x-beta)^(2) + beta(x-alpha)^(2) = 0` are:
View SolutionLet a,b and c be three distinct real roots of the cubic `x ^(3) +2x ^(2)-4x-4=0.` If the equation `x ^(3) +qx ^(2)+rx+le =0` has roots `1/a, 1/b and 1/c,` then the vlaue of `(q+r+s)` is equal to :
View SolutionSolution set of the inequality, `2-log_(2)(x^(2)+3x) ge0` is-
View SolutionFor what least integral 'k' is the quadratic trinomial `(k-2) x ^(2) + 8x + (k +4)` is positive for all ral values of x ?
View SolutionIf roots of the equation `(m-2)x^2-(8-2m)x-(8-3m)=0` are opposite in sign then the number of integral values of m is/are :
View SolutionIf `log _( 0.6) (log _(6) ((x ^(2) +x)/(x +4))) lt 0,` then complete set of value of 'x' is:
View SolutionTwo different real numbers `alpha and beta ` are the roots of the quadratic equation `ax ^(2) + c=0 a,c ne 0,` then ` alpha ^(3) + beta ^(3)` is:
View SolutionThe least integral value of 'k' for which `(k-1) x ^(2) -(k+1) x+ (k+1)` is positive for all real value of x is:
View SolutionIf `(-2, 7)` is the highest point on the graph of `y =-2x ^(2) -4ax+k,` then k equals :
View SolutionIf `a+b+c=0, a,b,c in Q` then roots of the equation `(b+c-a) x ^(2) + (c+a-c) =0` are:
View SolutionIf two roots of `x ^(3) -ax ^(2) + bx -c =0` are equal in magnitude but opposite in sign. Then:
View SolutionIf `alpha and beta` are the ral roots of `x ^(2) + px +q =0 and alpha ^(4), beta ^(4) ` are the roots of `x ^(2) - rx+s =0.` Then the equation `x ^(2) -4qx+2q ^(2)-r =0` has always `(alpha ne beta, p ne 0 , p,q, r, s in R)`:
View SolutionIf `(x^2+p x+1)` is a factor of `(a x 63+b x+c),t h e n` `a^2+c^2=-a b` b. `a^2-c^2=-a b` c. `a^2-c^2=a b` d. none of these
View SolutionIn a `Delta ABC tan ""A/2, tan ""B/2, tan ""C/2 ` are in H.P., then the value iof `cot ""A/2 cot ""C/2` is :
View SolutionQ. Let `f(x)=10-|x-10|` `AA`x`in[-9,9]` If M and m be the maximum and minimum value of f(x) respectively then
View SolutionSolution of the quadratic equation `(3 |x| -3) ^(2) = |x| +7, ` which belongs to the domain of the function `y = sqrt((x-4)x )` is :
View SolutionNumber of real solutions of the equation `x ^(2) +3|x| + 2 =0` is:
View SolutionIf the roots of `x^2-bx +c=0` are two consecutive integers then `b^2-4c=`
View SolutionIf x is real, then minimum vlaue of `(3x ^(2) + 9x +17)/(3x ^(2) +9x+7)` is:
View SolutionIf `(x^2+2x+7)/(2x+3)<6`, x`in` R then
View SolutionIf x is real, tehn range of `(3x -2)/(7x+5)` is :
View SolutionLet A denotes the set of values of x for which `(x+2)/(x-4) le0` and B denotes the set of values of x for which `x^2-ax-4 le 0`. If B is the subset of A then a cannot take integral value (a) 0, (b) 1 (c) 2 (d) 3
View SolutionIf the quadratic polynomial `P (x)=(p-3)x ^(2) -2px+3p-6` ranges from `[0,oo)` for every `x in R,` then the value of p can be:
View SolutionIf graph of the quadratic `y = ax ^(2)+bx+c` is given below :
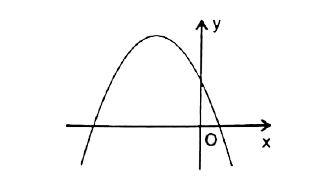 then:
then:
View SolutionIf quadratic equation `ax^2+bx+c=0` does not have real roots, then which of the following may be false (a) `a(a-b+c) gt 0` (b) `c(a- b+c)>0` e) `b(a- b+c) gt 0` (d) `a +b+c) (a-b+c)gt0`
View SolutionMinimum vlaues of `y = x ^(2) -3x+5, x in [-4, 1]` is:
View SolutionIf `3x^(2) -17x+10 =0 and x^(2)-5x+m =0` has a common root, then sum of all possible real values of 'm' is:
View SolutionFor real numbers x and y, if `x^2+xy-y^2+2x -y+1=0`, then (a) y can not be between 0 and `8/5` (b) y can not be between `-8/5 and 8/5` (c) y cannnot be between `-8/5 and 0`(d) y cannot be between `-16/5 and 0`
View SolutionIf `3x ^(4) -6x ^(3) +kx ^(2)-8x-12`is divisible by `x-3,` then it is also divisible by :
View SolutionThe complete set of values of a so that equation `sin^4 x+ a sin^2 x+ 4=0` has at least one real root is (A) `(- oo, -5]` (B) `(- oo , 4] uu [ 4, oo)` (C) `(-oo, -4]` (D) `[4, oo)`
View SolutionLet `r _(1) s_(1) t` be the roots of the equation `x ^(3) + ax ^(2) +bx+c=0,` such that `(rs )^(2) + (st)^(2) + (rt)^(2) =b^(2)-kac,` then k =
View SolutionIf the roots of the cubic `x ^(3) +ax ^(2) + bx +c=0` are three consecutive positive integers, then the value of `(a ^(2))/(b +1) =`
View SolutionLet 'k' be a real number. The minimum number of distinct real roots possible of the equation `(3x^2+kx+3)(x^2+kx-1)=0` is
View SolutionIf r and s are variables satisfying the equation `(1)/(r+s) =1/r+1/s. ` The value of `((r )/(s ))^(3)` is equal to :
View SolutionLet `f(x) = x^2 + ax + b`. If the maximum and the minimum values of f(x) are 3 and 2 respectively for `0 <= x <= 2`, then the possible ordered pair(s) of (a,b) is/are
View SolutionThe roots of the equation `|x^2-x-6|=x+2` are
View SolutionIf `a ,b ,c` be the sides of ` A B C` and equations `a x 62+b x+c=0a n d5x^2+12+13=0` have a common root, then find `/_Cdot`
View SolutionIf `alpha, beta and gamma` are three ral roots of the equatin `x ^(3) -6x ^(2)+5x-1 =0,` then the value of `alpha ^(4) + beta ^(4) + gamma ^(4)` is:
View SolutionIf one of the roots of the equation `2x^2-6x+k=0` is `((alpha+5i)/2)`, then the values of a and k are
View SolutionLet `x_1 and x_2` be the real roots of the equation `x^2 -(k-2)x+(k^2 +3k+5)=0` then the maximum value of `x_1^2+x_2^2` is
View SolutionThe set of values of a for which ` (a - 1) x^(2) - (a + 1) x + a - 1`
`ge 0 ` ture for all ` x ge 2` is
View SolutionIf ` alpha, beta` be the roots of `4x^2-17x+lambda=0, lambda in R` such that `1 lt alpha lt 2` and `2 lt beta lt 3` then the number of integral values of `lambda` is `
View SolutionAssume that p is a ral number. In order of `""^(3) sqrt(x+3p+1) -""^(3) sqrt(x ) =1` to have real solutions, it is necessary that:
View SolutionIf `alpha, beta` ar the roots of the quadratic equation `x ^(2) -(3+ 2 ^(sqrt(log _(2)3))-3 ^(sqrt(log _(3)2)))x-2 (3 ^(log _(3)2)-2^(log _(z)3))=0, ` then the value of `alpha ^(2) + alpha beta ` is equal to :
View SolutionIf `m` is the minimum value of `f(x , y)=x^2-4x+y^2+6y` when `xa n dy` are subjected to the restrictions `0lt=xlt=1a n d0lt=ylt=1,` then the value of `|m|` is________
View SolutionThe expression `ax^2+2bx+c`, where 'a' is non-zero real number, has same sign as that of 'a' for every real value of x,then roots of quadratic equation `ax^2+ (b-c) x-2b-c -a-0` are: (a) real and equal (b) real and unequal (c) non-real having positive real part(d) non-real having negative real part
View SolutionLet a,b and c be the roots of `x ^(3) -x+1 =0,` then the ralue of `((1)/(a+1)+(1)/(b+1)+(1)/(c+1))` equals to :
View SolutionThe number of integral values of k for which the inequality
`x^(2)-2(4k-1)x+15k^(2)-2k-7 ge0` hold for `x in R` are _____________
View SolutionThe number of integral values which can be taken by the expression, `f (x) = (x ^(3)-1)/((x-1) (x ^(2) -x+1))` for `x in R,` is:
View SolutionThe comlete set of values of m for which the inequality `(x ^(2) -mx-2)/( x ^(2) + mx +4)gt-1` is satisfied `aa x in R,` is :
View SolutionThe complete set of values of a for which the roots of the equatin `x ^(2) -2 |a+1| x|1 =0` are real is given by :
View SolutionIf the quadratic polynomials defined on real coefficient
`P(x)=a_(1)x^(2)+2b_(1)x+c_(1)` and `Q(x)=a_(2)x^(2)+2b_(2)x+c_(2)` take positive values `AA x in R`, what can we say for the trinomial `g(x)=a_(1)a_(2)x^(2)+b_(1)b_(2)x+c_(1)c_(2)` ?
View Solution
EXERCISE (SINGLE CHOICE PROBLEMS) questions and complete solutions for chapter QUADRATIC EQUATIONS of VK JAISWAL MATHS (HINGLISH) of Class 12