Complete Solutions to Exercise of chapter GEOMETRY of Class 6 book with complete answers and questions
| Class 6 | MATHS |
| Chapter | GEOMETRY |
| NCERT EXEMPLAR | Exercise |
| Number Of Questions | 56 |
| Academic Year | 2023-24 |
Name all the line segments in Fig. 2.24.

View SolutionName the line segments shown in Fig. 2.25.

View SolutionStatement the mid points of all the sides of Fig. 2.26

View SolutionName the vertices and the line segments in Fig. 2.27
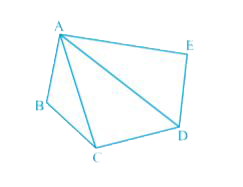
View SolutionWrite down fifteen angles (less than `180^(@)`) involved in Fig. 2.28
View SolutionName the following angles of Fig. 2.29, using three letters :
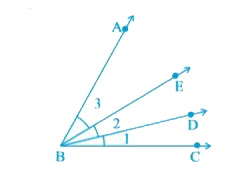
`angle1`
View SolutionName the following angles of Fig. 2.29, using three letters :
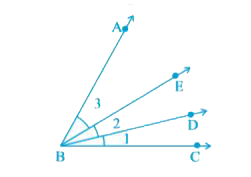
`angle2`
View SolutionName the following angles of Fig. 2.29, using three letters :

`angle3`
View SolutionName the following angles of Fig. 2.29, using three letters :
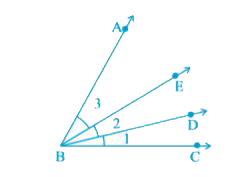
`angle1+angle2`
View SolutionName the following angles of Fig. 2.29, using three letters :
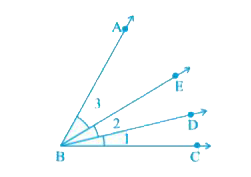
`angle2+angle3`
View SolutionName the following angles of Fig. 2.29, using three letters :
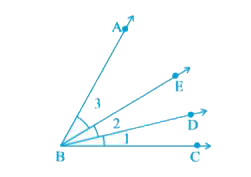
`angle1+angle2+angle3`
View SolutionName the following angles of Fig. 2.29, using three letters :
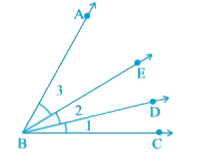
`angleCBA`-`angle1`
View SolutionName the point and then the line segments in each of the following figures (Fig. 2.30):

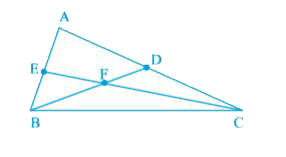
View SolutionWhich points in Fig. 2.31, appear to be mid - point of the line segments ? When you locate a mid - point, name the two equal oline segments formed by it

View SolutionIs it possible for the same line segment to have two different lengths ?
View SolutionIs it possible for the same
angle to have two different measures ?
View SolutionWill the measure of `angleABC` and of `angleCBD` make measure of `angleABD` in Fig. 2.32
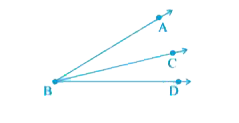
View SolutionWill the lenghts of line segment AB and line segment BC make the length of line segment AC in Fig. 2.33 ?

View SolutionDraw two acute angles and one obtuse angle without using a protractor. Estimate the measures of the angles. Measure them with the help of a protractor and see how much accurate is your estimate.
View SolutionLook at Fig. 2.34. Mark a point
(a) A which is in the interior of both `angle1` and `angle2`.
(b) B which is in the interior of only `angle1`.
(c ) Point C in the interior of `angle1`.
Now, state whether points B and C lie in the interior of `angle2` also.

View SolutionFind out the incorrect statement, if any, in the following An angle is formed when we have
(a) two rays with a common end-point
(b) two line segments with a common end - point
(c ) a ray and a line segment with a common end - point
View SolutionIn which of the following figures (Fig. 2.35),
(a) perpendicular bisector is shown ?
(b) bisector is shown ?
(c ) only bisector is shown ?
(d) only perpendicular is shown ?

View SolutionWhat is common in the following figures (i) and (ii) (Fig. 2.36.) ?

Is Fig. 2.36 (i) that of triangle ? If not why ?
View SolutionIf two rays intersect will their point of intersection be the vertex of an angle of which the rays are the two sides ?
View SolutionIn Fig. 2.37
name any four angles that appear to be acute angles.

View SolutionIn Fig. 2.37
name any two angles that appear to be obtuse angles.
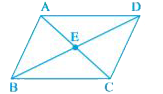
View SolutionIn Fig, 2.38,
(a) is `CA+CB=AB`? (b) is `BA+AC=CB` ?
(c ) is `AB+BC=CA` ?
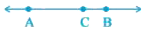
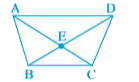
View SolutionIn Fig. 2.39
(a) What is `AE+EC` ?
(b) What is `AC-EC` ?
(c ) What is `BD-BE` ?
(d) What is `BD-DE` ?
View SolutionUsing the information given, name the right angles in each part of Fig. 2.40:
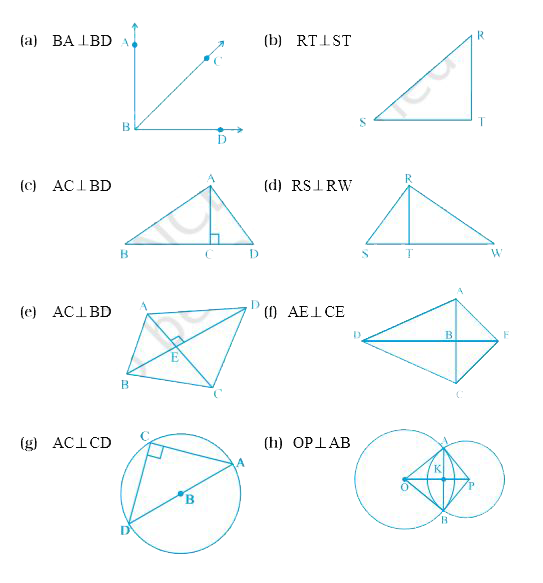
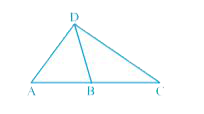
View SolutionWhat conclusion can be drawn from each part of Fig. 2.14, if
DB is the bisector of `angleADC` ?
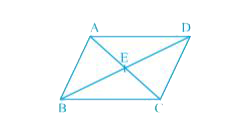
View SolutionWhat conclusion can be drawn from each part of Fig. 2.14, if
BD bisects `angleABC` ?
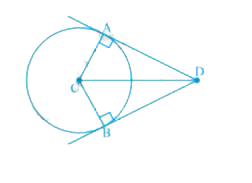
View SolutionWhat conclusion can be drawn from each part of Fig. 2.14, if
DC is the bisector of `angleADB,CA bot DA` and `CB bot DB` ?
View SolutionAn angle is said to be trisected, if it is divided into three equal parts. If in Fig. 2.42 into three equal parts. If in fig. 2.42, `angleBAC`=`angleCAD`=`angleDAE`, how many trisectors are there for `angleBAE` ?

View SolutionHow many points are marked in Fig 2.43 ?

View SolutionHow many line segments are threr in Fig. 2.43 ?

View SolutionIn Fig. 2.44, how many points are marked ? Name them.

View SolutionHow many line segments are there in Fig. 2.44 ? Name them.

View SolutionIn Fig 2.45 how many points are marked ? Name them.

View SolutionIn Fig 2.45 how many line segments are there ? Name them.

View SolutionIn Fig. 2.46, how many points are marked ? Name them.

View SolutionIn Fig. 2.46 how many line segments are there ? Name them.

View SolutionIn Fig. 2.47, O is the centre of the circle.
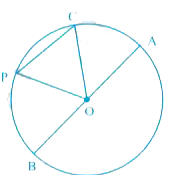
Name all chords of the circle.
View SolutionIn Fig. 2.47, O is the centre of the circle.
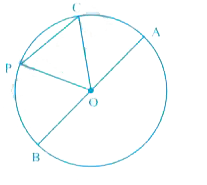
Name all radii of the circle.
View SolutionIn Fig. 2.47, O is the centre of the circle.

Name a chord, which is not the diameter of the circle.
View SolutionIn Fig. 2.47, O is the centre of the circle.
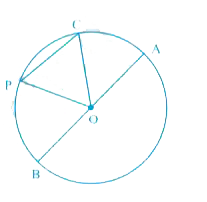
Shade sectors OAC and OPB.
View SolutionIn Fig. 2.47, O is the centre of the circle.
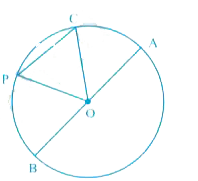
Shade the smaller segment of the circle formed by CP.
View SolutionCan we have two acute angles whose sum is
an acute angle ? Why or why not ?
View SolutionCan we have two acute angles whose sum is
a right angle ? Why or why not ?
View SolutionCan we have two acute angles whose sum is
an obtuse angle ? Why or why not ?
View SolutionCan we have two acute angles whose sum is
a straight angle ? Why or why not ?
View SolutionCan we have two acute angles whose sum is
a reflex angle ? Why or why not ?
View SolutionCan we have two obtuse angles whose sum is
a reflex angle ? Why or why not ?
View SolutionCan we have two obtuse angles whose sum is
a complete angle ? Why or why not ?
View SolutionWrite the name of
(a) vertices
(b) edges , and
(c ) faces of the prism shown in Fig. 2.48
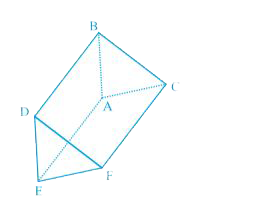
View SolutionHow many edges, faces and vertices are there in a sphere ?
View SolutionDraw all the diagonals of a pentagon ABCDE and name them.
View Solution
Exercise questions and complete solutions for chapter GEOMETRY of NCERT EXEMPLAR of Class 6
All Exercises from NCERT EXEMPLAR Class 6 MATHS GEOMETRY
- Exercise
- Exercise (Fill in the blanks to make the statements true:)
- Exercise (Out of foure options only one is correct. Write the correct answer.)
- Exercise (State whether the statements given in questions are true (T) or false (F):)
- Solved Examples
- Solved Examples (In examples 3 and 4, fill in the blanks to make the statements true :)
- Solved Examples (In examples 5 to 7, state whether the statements are true or false.)