Complete Solutions to All Questions of chapter BASIC GEOMETRICAL CONCEPTS of Class 6 book with complete answers and questions
| Class 6 | MATHS |
| Chapter | BASIC GEOMETRICAL CONCEPTS |
| Mathematics | All Questions |
| Number Of Questions | 40 |
| Academic Year | 2023-24 |
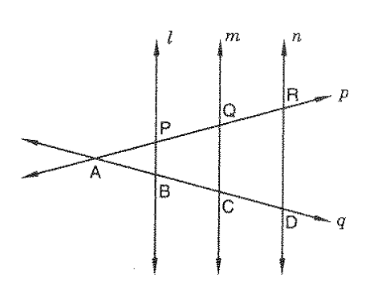
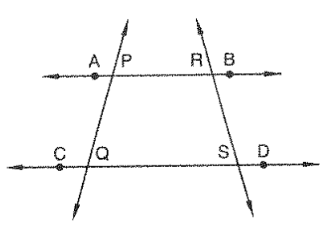
From Figure, name
(i)All pairs of parallel lines.
(ii)all pairs of intersecting lines.
(iii)ines of whose point of intersection in `P`
(iv)lines whose point of intersection in `C`
(v)lines whose point of intersection in `R`
(vi)Collinear points.
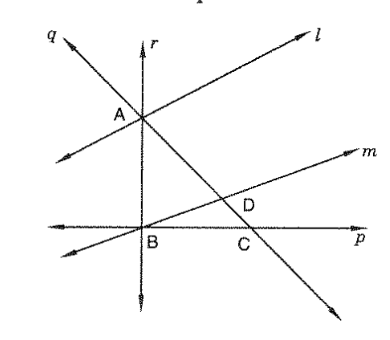
View SolutionFrom Figure, write
(i)Lines intersecting at `A`
(ii)Lines intersecting at `B`
(iii)Concurrent lines and their point of concurrence.
View SolutionMark three points in your notebook and name them.
View SolutionDraw a line in your notebook and name it using a small letter of the alphabet.
View SolutionDraw a line in your notebook and name it by taking any two points on it.
View SolutionGive three examples from your environment of: (i)Points (ii) Portion of a line (iii)Plane surfaces (iv) portion of a plane (v)Curved surfaces
View SolutionThere are a number of ways by which we can visualise a portion of a line. State whether the following represent a portion of a line or not: A piece of elastic stretched to the breaking point. Wire between two electric poles. The line thread by which a spider lowers itself.
View SolutionCan you draw a line on the surface of a sphere which lies wholly on it?
View SolutionMark a point on a sheet of paper and draw a line passing through it. How many lines can you draw through this point?
View Solutionmark any two points `P\ a n d\ Q` in your note book and draw a line passing through the points. How many lines can you draw passing through both the points?
View SolutionGiven an example of a horizontal plane and a vertical plane from your environment.
View SolutionHow many lines may pass through one given point, two given points, any three collinear points?
View SolutionIs it ever possible for exactly one line to pass through three points?
View SolutionExplain why it is not possible for a line to have a mid-point.
View SolutionMark three non-collinear points `A ,\ B\ a n d\ C` in your not book. Draw lines through these points taking two at time. Name these lines. How many such different lines can be drawn?
View SolutionCoplanar points are the points that are in the same plane. Thus, Can 150 points be coplanar? Can 3 points be non-coplanar?
View SolutionUsing a ruler, check whether the following points given in fig. 10.20 are collinear or not:
(i)D, A and C (ii) A, B and C (iii)A, B and E (iv) B, C and E

View SolutionLines `p ,\ q` are coplanar. So are the lines `p ,\ r` . Can conclude that the lines `p ,\ q ,\ r` are coplanar?
View SolutionGiven three examples each of : (a) intersecting lines (b)parallel lines from your environment.
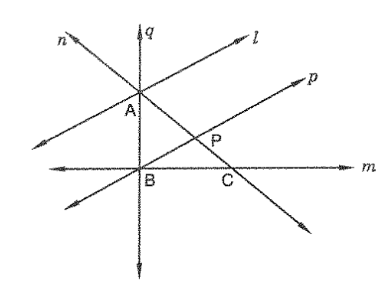
View SolutionForm Fig., write
(i)all pairs of parallel lines. (ii)all pairs of intersection lines. (iii)lines whose point of intersection is `l` . (iv) lines whose point of intersection is `D` . (v) lines whose point of intersection is `E` . (vi) lines whose point of intersection is `A` .
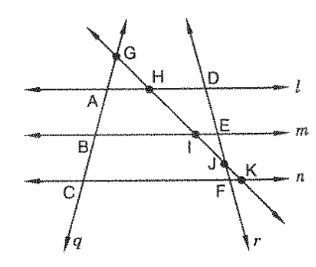
View SolutionFrom Fig., write concurrent lines and their points of concurrence.
View SolutionMark four points `A ,\ B ,\ C\ a n d\ D` in your notebook such that no three of them are collinear. Draw all the lines which join them in pairs as shown in Fig.
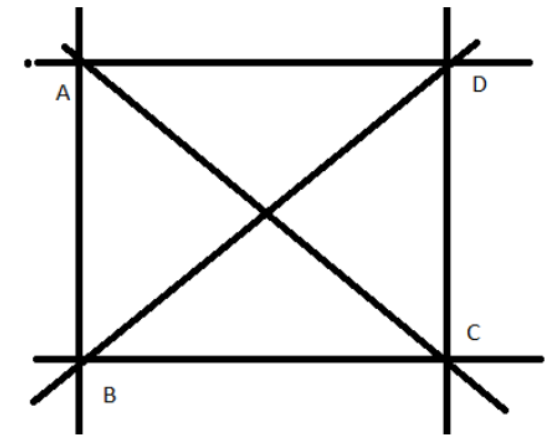
How many such lines can be drawn? Write the names of these lines. Name the lines which are concurrent at `A` .
View SolutionWhat is the maximum number of points of intersection of three lines in a plane? What is the minimum number?
View SolutionWith the help of figure, find the maximum and minimum number of points of intersection of four lines in a plane.
View SolutionLines `p ,\ q\ a n d\ r` are concurrent. Also, lines `p ,\ r\ a n d\ s` are concurrent. Draw a figure and state whether lines `p ,\ q ,\ r\ a n d\ s` are concurrent or not.
View SolutionLines `p ,\ q\ a n d\ r` are concurrent. Also lines `p ,\ s\ a n d\ t` are concurrent. Is always true that the lines `q ,\ r\ a n d\ s` will be concurrent? Is it always true for lines `q ,\ r\ a n d\ t` ?
View SolutionFill in the blanks in the following statements using suitable words: (a) A page of a book is a physical example of a …… (b) An inkpot has both…. surfaces (c) Two lines in a plane are either ….or are…..
View SolutionIdentify rays and line segments form the following figures:

View SolutionHow many line segments are there in each of the following figures? Name all of them.
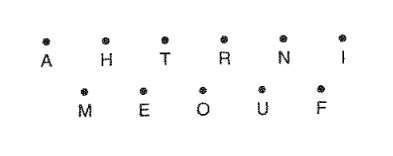
View SolutionIn Fig. points are given in two rows. Join the points `AM , HE ,TO,RUN,IF` . How many line segments are formed?
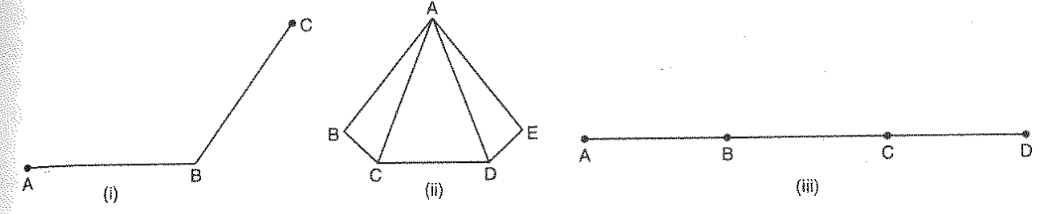
View SolutionIn Fig., name: Five line segments. (ii) Five rays (iii) Non-intersection line segments
View SolutionIn each of the following cases, state whether you can draw line segments on the given surfaces: The face of a cuboid. The surface of an egg or apple. The curved surface of a cylinder. The curved surface of a cone. The base of a cone.
View SolutionMark the following points on a sheet of paper. Tell how many line segments can be obtained in each case: Two points A, B. Three non-collinear points A, B, C. Four points such that no three of them belong to the same line. Any five points so that on three of them are collinear.
View SolutionCount the number of line segments in Fig.

View SolutionIn Fig.,

name all rays with initial points as `A ,\ B\ a n d\ C` respectively. Is ray ` A B ` different from ray ` A C ` ? Is ray ` B A ` different from ray ` C A ` ? Is ray ` C P ` different from ray ` C Q ` ?
View SolutionGive three examples of line segments from your environment.
View SolutionDraw rough diagrams to illustrate the following: (i) Open curve (ii) Closed curve
View SolutionClassify the following curves as open or closed:
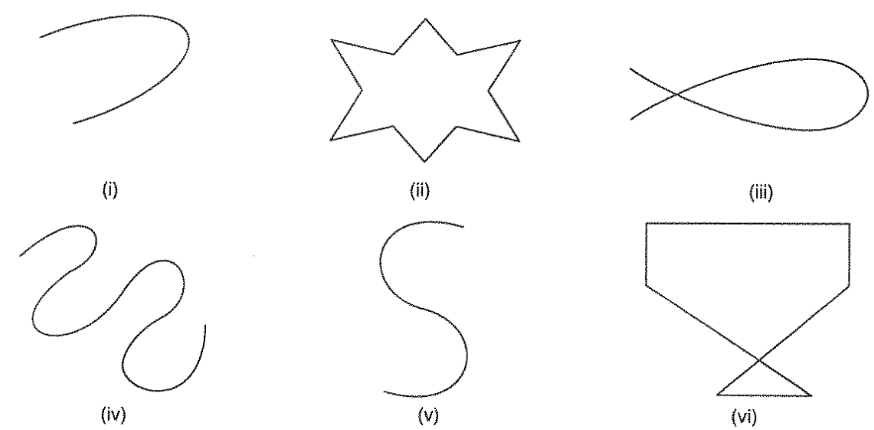
View SolutionDraw any polygon and shade its interior.
View SolutionIllustrate, if possible, each one of the following with a rough diagram: (a) A closed curve that is not a polygon. (b) An open curve made up entirely of line segments. (c) A polygon with two sides.
View Solution
All Questions questions and complete solutions for chapter BASIC GEOMETRICAL CONCEPTS of RD SHARMA MATHS (ENGLISH) of Class 6