Complete Solutions to PROBLEM of chapter पायथागोरसचा सिद्धान्त of Class 7 book with complete answers and questions
| Class 7 | MATHS |
| Chapter | पायथागोरसचा सिद्धान्त |
| NAVNEET PUBLICATION | PROBLEM |
| Number Of Questions | 14 |
| Academic Year | 2023-24 |
काटकोन '/_\PQR' मध्ये '/_P= 90°' जर '/(PQ) = 24' सेमी आणि '/ (PR) = 10' सेमी, तर रेख 'QR' ची लांबी काढा.`
View Solutionकाटकोन '/_\LMN' मध्ये, '/_M = 90°' जर 'l (LM) = 12' सेमी आणि 'l (LN) = 20 सेमी', तर रेख 'MN' ची लांबी काढा.`
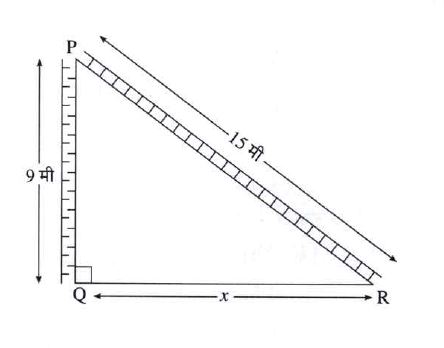
View Solution15 मी लांबीची शिडी जमिनीपासून 9 मीटर उंचीवरील एका खिडकीपाशी पोहोचते, तर भिंतीचा पाया व शिडीचे खालचे टोक यांच्यामधील अंतर काढा.` :
View Solutionपुढे काही त्रिकुटे दिली आहेत, त्यांतील पायथागोरसचे त्रिकुट ठरवा :
`3,4,5`
View Solutionपुढे काही त्रिकुटे दिली आहेत, त्यांतील पायथागोरसचे त्रिकुट ठरवा :
`2,4,5`
View Solutionपुढे काही त्रिकुटे दिली आहेत, त्यांतील पायथागोरसचे त्रिकुट ठरवा :
`4,5,6`
View Solutionपुढे काही त्रिकुटे दिली आहेत, त्यांतील पायथागोरसचे त्रिकुट ठरवा :
`2,6,7`
View Solutionपुढे काही त्रिकुटे दिली आहेत, त्यांतील पायथागोरसचे त्रिकुट ठरवा :
`9,40,41`
View Solutionपुढे काही त्रिकुटे दिली आहेत, त्यांतील पायथागोरसचे त्रिकुट ठरवा :
`4,7,8`
View Solutionपुढे काही त्रिकोणांच्या बाजू दिल्या आहेत, त्यावरून कोणते त्रिकोण काटकोन त्रिकोण आहेत, ते ओळखा :
(दिलेल्या बाजूंपैकी सर्वांत मोठ्या बाजूचा वर्ग इतर दोन बाजूंच्या वर्गाच्या बेरजेइतका असेल, तर त्या बाजूंनी तयार होणारा त्रिकोण काटकोन त्रिकोण असतो.)'
`8,15,17`
View Solutionपुढे काही त्रिकोणांच्या बाजू दिल्या आहेत, त्यावरून कोणते त्रिकोण काटकोन त्रिकोण आहेत, ते ओळखा :
(दिलेल्या बाजूंपैकी सर्वांत मोठ्या बाजूचा वर्ग इतर दोन बाजूंच्या वर्गाच्या बेरजेइतका असेल, तर त्या बाजूंनी तयार होणारा त्रिकोण काटकोन त्रिकोण असतो.)
`11,12,15`
View Solutionपुढे काही त्रिकोणांच्या बाजू दिल्या आहेत, त्यावरून कोणते त्रिकोण काटकोन त्रिकोण आहेत, ते ओळखा :
(दिलेल्या बाजूंपैकी सर्वांत मोठ्या बाजूचा वर्ग इतर दोन बाजूंच्या वर्गाच्या बेरजेइतका असेल, तर त्या बाजूंनी तयार होणारा त्रिकोण काटकोन त्रिकोण असतो.)
`11,60,61`
View Solutionपुढे काही त्रिकोणांच्या बाजू दिल्या आहेत, त्यावरून कोणते त्रिकोण काटकोन त्रिकोण आहेत, ते ओळखा :
(दिलेल्या बाजूंपैकी सर्वांत मोठ्या बाजूचा वर्ग इतर दोन बाजूंच्या वर्गाच्या बेरजेइतका असेल, तर त्या बाजूंनी तयार होणारा त्रिकोण काटकोन त्रिकोण असतो.)
`1.5,1.6,1.7`
View Solutionपुढे काही त्रिकोणांच्या बाजू दिल्या आहेत, त्यावरून कोणते त्रिकोण काटकोन त्रिकोण आहेत, ते ओळखा :
(दिलेल्या बाजूंपैकी सर्वांत मोठ्या बाजूचा वर्ग इतर दोन बाजूंच्या वर्गाच्या बेरजेइतका असेल, तर त्या बाजूंनी तयार होणारा त्रिकोण काटकोन त्रिकोण असतो.)
`40,20,30`
View Solution
PROBLEM questions and complete solutions for chapter पायथागोरसचा सिद्धान्त of NAVNEET PUBLICATION of Class 7