Complete Solutions to EXAMPLE of chapter CONGRUENCE OF TRIANGLES of Class 7 book with complete answers and questions
| Class 7 | MATHS |
| Chapter | CONGRUENCE OF TRIANGLES |
| PSEB | EXAMPLE |
| Number Of Questions | 85 |
| Academic Year | 2023-24 |
`triangleABC` and `trianglePQR` are congruent under the correspondence:
`ABC harr RQP`
Write the parts of `triangleABC` that correspond to
`barPQ`
View Solution`triangleABC` and `trianglePQR` are congruent under the correspondence:
`ABC harr RQP`
Write the parts of `triangleABC` that correspond to
`angleQ`
View Solution`triangleABC` and `trianglePQR` are congruent under the correspondence:
`ABC harr RQP`
Write the parts of `triangleABC` that correspond to
`barRP`
View SolutionWhen two triangles, say ABC and PQR are given, there are, in all, six possible matchings or correspondences. Two of them are
(i) ABC PQR and (ii) ABC QRP.
Find the other four correspondences by using two cutouts of triangles. Will all these correspondences lead to congruence? Think about it.
View SolutionComplete the following statements:
Two line segments are congruent if ___________.
View SolutionComplete the following statements:
Among two congruent angles, one has a measure of `70^@` , the measure of the other angle is ___________.
View SolutionComplete the following statements:
When we write `angleA = angleB`, we actually mean_______.
View SolutionGive any two real-life examples for congruent shapes.
View SolutionIf `triangleABC~= triangleFED` under the correspondence `ABC harr FED`, write all the corresponding congruent parts of the triangles.
View SolutionIn `triangleDEF ~= triangleBCA`, write the part(s) of `triangleBCA` that correspond to
`angleE`
View SolutionIn `triangleDEF ~= triangleBCA`, write the part(s) of `triangleBCA` that correspond to
`barEF`
View SolutionIn `triangleDEF ~= triangleBCA`, write the part(s) of `triangleBCA` that correspond to
`angleF`
View SolutionIn `triangleDEF ~= triangleBCA`, write the part(s) of `triangleBCA` that correspond to
`barDF`
View SolutionIn triangles ABC and PQR, AB = 3.5 cm, BC = 7.1 cm, AC = 5 cm, PQ = 7.1 cm, QR = 5 cm and PR = 3.5 cm. Examine whether the two triangles are congruent or not. If yes, write the congruence relation in symbolic form.

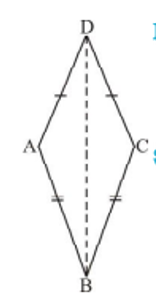
View SolutionIn fig Ad = CD and AB = CB.
State the three pairs of equal parts in `triangleABD` and `triangleCBD`.
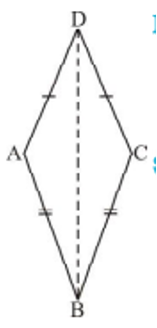
View SolutionIn fig Ad = CD and AB = CB.
Is `triangleABD ~= triangleCBD`? Why or why not?
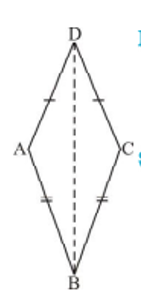
View SolutionIn fig Ad = CD and AB = CB.
Does BD bisect `angleABC`? Give reasons.
View SolutionIn Fig, lengths of the sides of the triangles are indicated. By applying the SSS congruence rule, state which pairs of triangles are congruent. In case of congruent triangles, write the result in symbolic form:
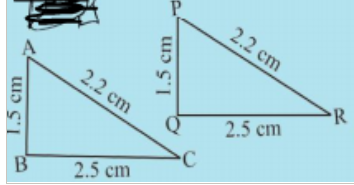
View SolutionIn Fig, lengths of the sides of the triangles are indicated. By applying the SSS congruence rule, state which pairs of triangles are congruent. In case of congruent triangles, write the result in symbolic form:
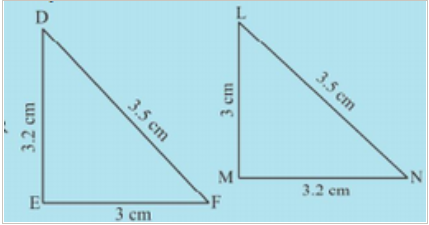
View SolutionIn Fig, lengths of the sides of the triangles are indicated. By applying the SSS congruence rule, state which pairs of triangles are congruent. In case of congruent triangles, write the result in symbolic form:
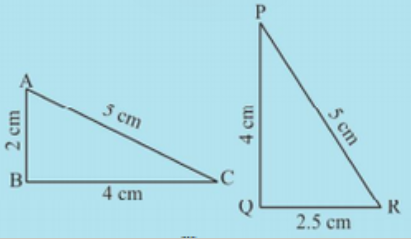
View SolutionIn Fig, lengths of the sides of the triangles are indicated. By applying the SSS congruence rule, state which pairs of triangles are congruent. In case of congruent triangles, write the result in symbolic form:
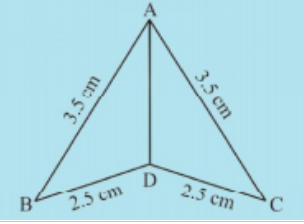
View SolutionIn Fig, AB = AC and D is the mid-point of `barBC`.

State the three pairs of equal parts in `triangle ADB` and `triangleADC`.
View SolutionIn Fig, AB = AC and D is the mid-point of `barBC`.

Is `triangleADB ~= triangleADC`? Give reasons.
View SolutionIn Fig, AB = AC and D is the mid-point of `barBC`.

Is `angleB = angleC`? Why?
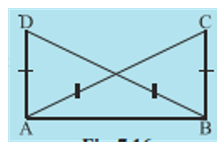
View SolutionIn Fig, Ac = BD and AD = BC. Which of the following statements is meaningfully written?
View SolutionABC is an isosceles triangle with AB = AC.Take a trace-copy of ABC and also name it as ABC.
State the three parts of equal parts in `triangleABC` and `triangleACB`.
View SolutionABC is an isosceles triangle with AB = AC.Take a trace-copy of ABC and also name it as ABC.

Is `angleB = angleC`? Why or why not?
View SolutionGiven below are measurements of some parts of two triangles. Examine whether the two triangles are congruent or not, by using SAS congruence rule. If the triangles are congruent, write them in symbolic form.
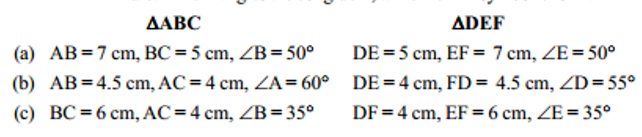 (It will be always helpful to draw a rough figure, mark the measuremants and then probe the question).
(It will be always helpful to draw a rough figure, mark the measuremants and then probe the question).
View SolutionIn Fig AB = AC and AD is the bisector of `angleBAC`.

State three pairs of equal parts in triangles ADB and ADC.
View SolutionIn Fig AB = AC and AD is the bisector of `angleBAC`.

Is `triangleADB ~= triangleADC`? Give reasons.
View SolutionIn Fig AB = AC and AD is the bisector of `angleBAC`.

Is `angleB = angleC`? Give reasons.
View SolutionWhich angle is included between the sides `barDE` and `barEF` of `triangleDEF`?
View SolutionBy applying SAS congruence rule, you want to establish that `trianglePQR~= triangleFED`. It is given that PQ = FE and RP = DF. What additional information is needed to establish the congruence?
View SolutionIn Fig , measures of some parts of the triangles are indicated. By applying SAS congruence rule, state the pairs of congruent triangles, if any, in each case. In case of congruent triangles, write them in symbolic form.
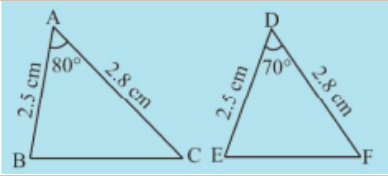
View SolutionIn Fig , measures of some parts of the triangles are indicated. By applying SAS congruence rule, state the pairs of congruent triangles, if any, in each case. In case of congruent triangles, write them in symbolic form.

View SolutionIn Fig , measures of some parts of the triangles are indicated. By applying SAS congruence rule, state the pairs of congruent triangles, if any, in each case. In case of congruent triangles, write them in symbolic form.

View SolutionIn Fig , measures of some parts of the triangles are indicated. By applying SAS congruence rule, state the pairs of congruent triangles, if any, in each case. In case of congruent triangles, write them in symbolic form.
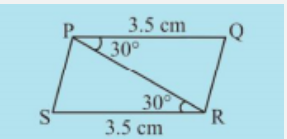
View SolutionIn Fig `bar AB` and `bar CD` bisect each other at O.

State the three pairs of equal parts in two triangles AOC and BOD.
View SolutionIn Fig `bar AB` and `bar CD` bisect each other at O.

Which of the following statements are true?
`triangleAOC ~= triangleDOB`
View SolutionIn Fig `bar AB` and `bar CD` bisect each other at O.

Which of the following statements are true?
`triangleAOC ~= triangleBOD`
View SolutionBy applying ASA congruence rule, it is to be established that `triangleABC ~= triangleQRP` and it is given that BC = RP. What additional information is needed to establish the congruence?
View SolutionIn Fig,can you use ASA congruence rule and conclude that `triangleAOC ~= triangleBOD`?
View SolutionWhat is the side included between the angles M and N of `triangleMNP`?
View SolutionYou want to establish `triangleDEF~= triangleMNP`, using the ASA congruence rule. You are given that `angleD = angleM` and `angleF = angleP`. What information is needed to establish the congruence? (Draw a rough figure and then try!
View SolutionIn Fig, measures of some parts are indicated. By applying ASA congruence rule, state which paris of triangles are congruent. In case of congruence write the result in symoblic form.
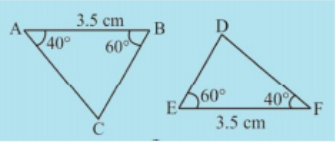
View SolutionIn Fig, measures of some parts are indicated. By applying ASA congruence rule, state which paris of triangles are congruent. In case of congruence write the result in symoblic form.
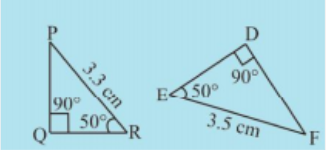
View SolutionIn Fig, measures of some parts are indicated. By applying ASA congruence rule, state which paris of triangles are congruent. In case of congruence write the result in symoblic form.

View SolutionIn Fig, measures of some parts are indicated. By applying ASA congruence rule, state which paris of triangles are congruent. In case of congruence write the result in symoblic form.
View SolutionGiven below are measurements of some parts of two triangles Examine whether the two triangles are congruent or not, by ASA congruence rule. In case of congruence, write it in symbolic form.
View SolutionIn Fig, ray AZ bisects `angleDAB` as well as `angleDCB`.
State the three pairs of equal parts in triangles BAC and DAC.
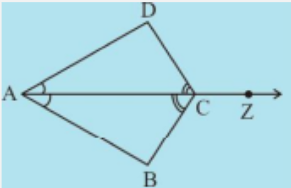
View SolutionIn Fig, ray AZ bisects `angleDAB` as well as `angleDCB`.
Is `triangleBAC ~=triangleDAC`? Give reasons.

View SolutionIn Fig, ray AZ bisects `angleDAB` as well as `angleDCB`.
Is AB = AD? Justify you answer.

View SolutionIn Fig, ray AZ bisects `angleDAB` as well as `angleDCB`.
Is CD = CB? Give reasons.
View SolutionSolve
`x^2-7x+6=0`
View SolutionIn Fig, `DA bot AB`, `CB bot AB` and AC = BD. State the three pairs of equal parts in `triangleABC` and `triangleDAB`. Which of the following statements is meaningful?

`triangleABC ~=triangleBAD`
View SolutionIn Fig, `DA bot AB`, `CB bot AB` and AC = BD. State the three pairs of equal parts in `triangleABC` and `triangleDAB`. Which of the following statements is meaningful?

`triangleABC ~= triangleABD`
View SolutionIn Fig measures of some parts of triangles are given. By applying RHS congruence rule, state which pairs of triangles are congruent. In case of congruent traingles, write the result in symbolic form.
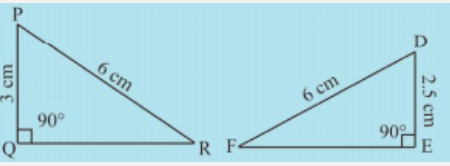
View SolutionIn Fig measures of some parts of triangles are given. By applying RHS congruence rule, state which pairs of triangles are congruent. In case of congruent traingles, write the result in symbolic form.
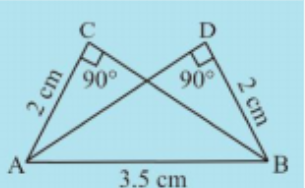
View SolutionIn Fig measures of some parts of triangles are given. By applying RHS congruence rule, state which pairs of triangles are congruent. In case of congruent traingles, write the result in symbolic form.
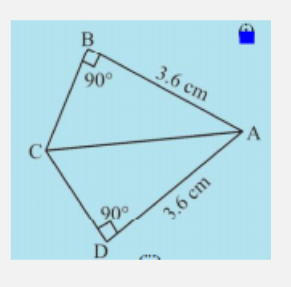
View SolutionIn Fig measures of some parts of triangles are given. By applying RHS congruence rule, state which pairs of triangles are congruent. In case of congruent traingles, write the result in symbolic form.
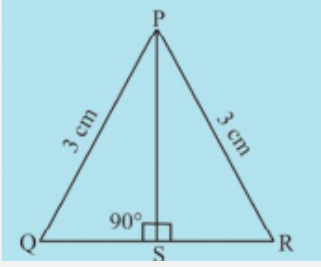
View SolutionIt is to be established by RHS congruence rule that `triangle ABC ~= triangleRPQ`. What additional information is needed, if it is given that
`angleB= angleP` and AB = RP?
View SolutionIn Fig
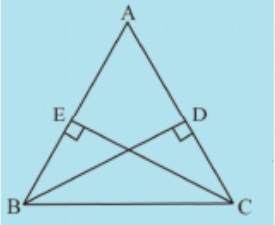
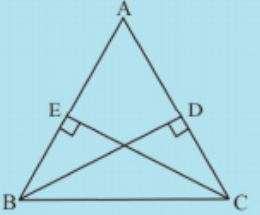
BD and CE are altitudes of `triangleABC` such that BD = CE.
State the three pairs in `triangleCBD` and `triangleBCE`.
View SolutionIn Fig, BD and CE are altitudes of `triangleABC` such that BD = CE.
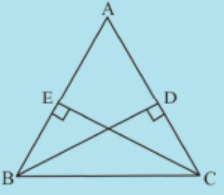
Is `triangleCBD ~= triangleBCE`? Why or why not?
View SolutionIn Fig, BD and CE are altitudes of `triangleABC` such that BD = CE.
Is `angleDCB = angleEBC`? Why or why not?
View SolutionABC is an isosceles triangle with AB = AC and AD is one of its altitudes.
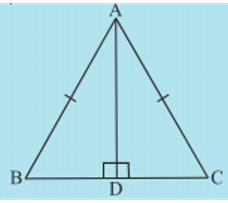
State the three pairs of equal parts in `triangleADB` and `triangleADC`.
View SolutionABC is an isosceles triangle with AB = AC and AD is one of its altitudes.

Is `triangleADB ~= triangleADC`? Why or why not?
View SolutionABC is an isosceles triangle with AB = AC and AD is one of its altitudes.

Is `angleB = angleC`? Why or why not?
View SolutionABC is an isosceles triangle with AB = AC and AD is one of its altitudes.

Is BD = CD? Why or why not?
View SolutionWhich congruence criterion do you use in the following?
Given: Given: AC = DF
AB = DE
BC = EF So, `triangleABC ~= triangleDEF`

View SolutionWhich congruence criterion do you use in the following?
Given: ZX = RP
RQ = ZY
`anglePRQ = angleXZY`
So, `trianglePQR ~= triangleXYZ`

View SolutionWhich congruence criterion do you use in the following?
Given:
`angleMLN = angleFGH`
`angleNML = angleGFH
`, `ML = FG`
So, `triangleLMN ~=triangleGFH`
View SolutionWhich congruence criterion do you use in the following?
Given: EB = DB
AE = BC
`angleA = angleC = 90^@`
So, `triangleABE ~= triangleCDB`

View SolutionYou want to show that `triangleART ~= trianglePEN`, (i) AR = (ii) RT= (iii)AT =
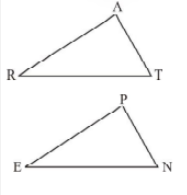
View SolutionYou want to show that `triangleART ~=trianglePEN`, If it is given that `angleT = angleN` and you are to use SAS criterion, you need to have (i) RT= and (ii) PN =

View SolutionYou want to show that `angleART ~=anglePEN`,

If you have SSS criterion, (i) AR= (ii)RT= (iii) AT= ?
View SolutionYou have to show that `triangleAMP ~= triangleAMQ`.
In the following proof, supply the missing reasons.

View SolutionIn `triangleABC, angleA = 30^@`, `angleB=40^@` and `angleC=110^@`
In `trianglePQR, angleP = 30^@`, `angleQ= 40^@` and `angleR= 110^@`
A student says that `triangleABC ~=trianglePQR` by AAA congruence criterion. Is he justified? Why or why not?
View SolutionIn the figure, the two triangles are congruent. The corresponding parts are marked. We can write `triangleRAT ~=?`
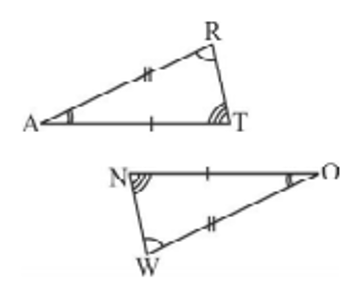
View SolutionComplete the congruence statement:
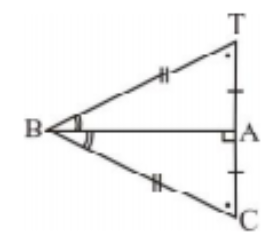
`triangleBCA ~=?`
View SolutionComplete the congruence statement:
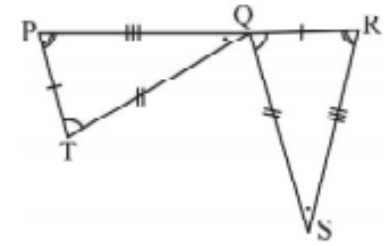
`triangleQRS ~=?`
View SolutionIn a squared sheet, draw two triangles of equal areas such that
the triangles are congruent. What do you say about its perimeters?
View SolutionIn a squared sheet, draw two triangles of equal areas such that
the triangles are not congruent. What do you say about its perimeters?
View SolutionDraw a rough sketch of two triangles such that they have five pairs of congruent parts but still the triangles are not congruent.
View SolutionIf `triangleABC` and `trianglePQR` are to be congruent, name one additional pair of corresponding parts. What criterion did you use?
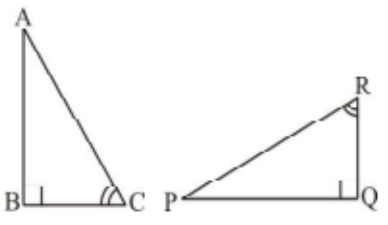
View SolutionExplain, why `triangleABC ~= triangleFED`.
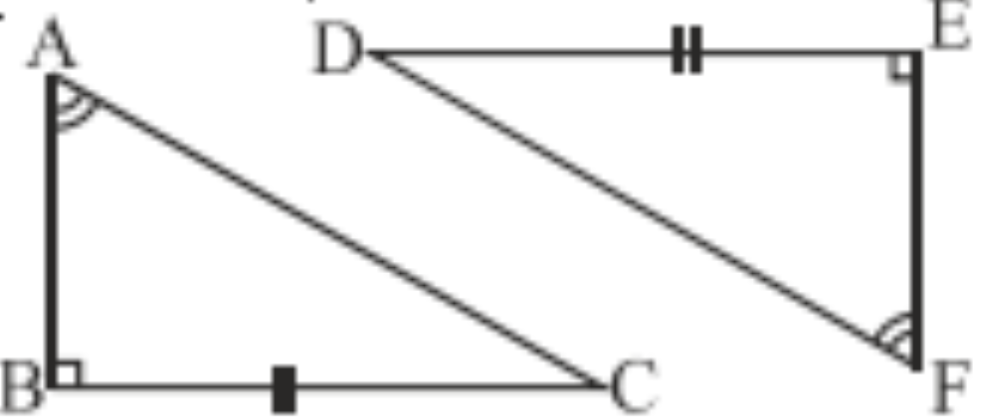
View Solution
EXAMPLE questions and complete solutions for chapter CONGRUENCE OF TRIANGLES of PSEB of Class 7