Complete Solutions to EXAMPLE of chapter Understanding Quadrilaterals. of Class 8 book with complete answers and questions
| Class 8 | MATHS |
| Chapter | Understanding Quadrilaterals. |
| ASHOK PUBLICATION ASSAM | EXAMPLE |
| Number Of Questions | 83 |
| Academic Year | 2023-24 |
Given here are some figures.
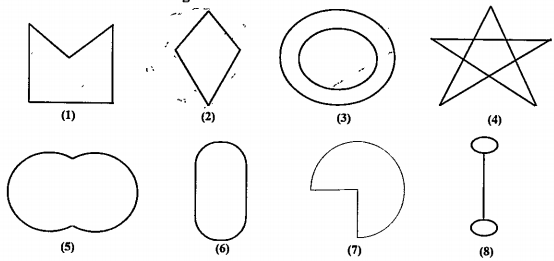
Classify each of them on the basis of the following.
Simple curve
View SolutionGiven here are some figures.

Classify each of them on the basis of the following.
Simple curve
View SolutionGiven here are some figures.

Classify each of them on the basis of the following.
Convex polygon
View SolutionGiven here are some figures.

Classify each of them on the basis of the following.
Concave polygon.
View SolutionHow many diagonals does each of the following have?
A convex quadrilateral.
View SolutionHow many diagonals does each of the following have?
A regular hexagon
View SolutionHow many diagonals does each of the following have?
A triangle
View SolutionWhat is the sum of the measures of the angles of a convex quadrilateral? Will this property hold if the quadrilateral is not convex? (Make non-convex quadrilateral and try!)
View SolutionExamine the table. (Each figure is divided into triangles and the sum of the angles deduced from that.)
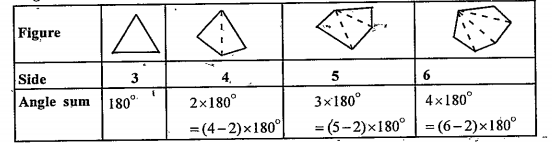
What can you say about the angle sum of a convex polygon with number of sides?
7
View SolutionExamine the table. (Each figure is divided into triangles and the sum of the angles deduced from that.)

What can you say about the angle sum of a convex polygon with number of sides?
8
View SolutionExamine the table. (Each figure is divided into triangles and the sum of the angles deduced from that.)
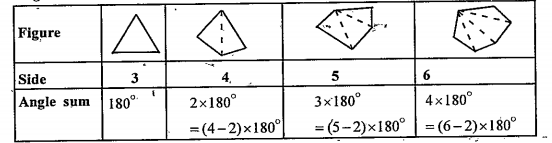
What can you say about the angle sum of a convex polygon with number of sides?
10
View SolutionExamine the table. (Each figure is divided into triangles and the sum of the angles deduced from that.)
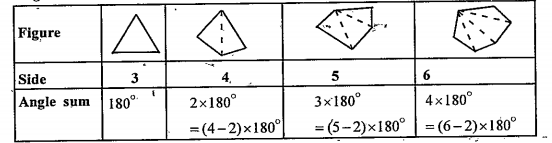
What can you say about the angle sum of a convex polygon with number of sides?
n
View SolutionWhat is regular polygon?
State the name of a regular polygon of
3 sides
View SolutionWhat is regular polygon?
State the name of a regular polygon of
4 sides
View SolutionWhat is regular polygon?
State the name of a regular polygon of
6 sides
View SolutionFind the angle measure x in the following figures.
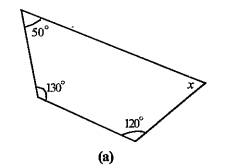
View SolutionFind the angle measure x in the following figures.
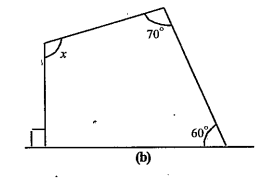
View SolutionFind the angle measure x in the following figures.
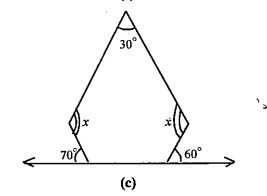
View SolutionFind the angle measure x in the following figures.

View Solution
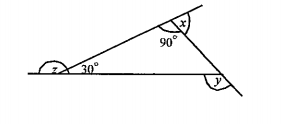
Find
`x+y+z`
View Solution
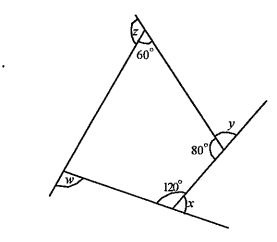
Find
`x+y+z+w`
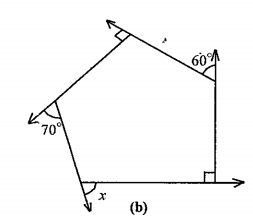
View SolutionFind x in the folloiwng figures.
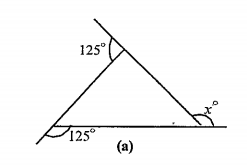
View SolutionFind x in the folloiwng figures.
View SolutionFind the measure of each exterior angle of a regular polygon of
9 sides
View SolutionFind the measure of each exterior angle of a regular polygon of
15 sides
View SolutionHow many sides does a regular polygon have if the measure of an exterior angle is `24^@`?
View SolutionHow many sides does a regular polygon have if each of its interior angles is `165^@`?
View SolutionIs it possible to have a regular polygon with measure of each exterior angle as `22^@`?
View SolutionCan 22 degree be an interior angle of a regular polygon? Why?
View SolutionWhat is the minimum interior angle possible for a regular polygon? Why?
View SolutionWhat is the maximum exterior angle possible for a regular polygon?
View SolutionGiven a parallelogram ABCD, Complete each statement along with the definition or property used.

AD = ________
View SolutionGiven a parallelogram ABCD, Complete the statement along with the definition or property used.

`angle DCB` = ___________
View SolutionGiven a parallelogram ABCD, Complete each statement along with the definition or property used.

AD = ________
View SolutionGiven a parallelogram ABCD, Complete each statement along with the definition or property used.
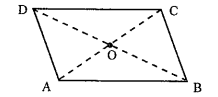
`mangleDAB + mangleCDA` = _________
View SolutionConsider the following parallelograms. Find the values of the unknowns x, y, z.
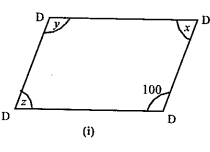
View SolutionConsider the following parallelograms. Find the values of the unknowns x, y, z.
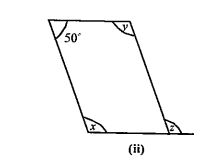
View SolutionConsider the following parallelograms. Find the values of the unknowns x, y, z.

View SolutionConsider the following parallelograms. Find the values of the unknowns x, y, z.
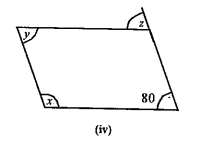
View SolutionConsider the following parallelograms. Find the values of the unknowns x and y.
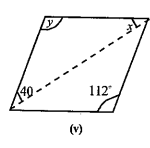
View SolutionCan a quadrilateral ABCD be a parallelogram, if
`angleD + angleB = 180^@`?
View SolutionCan a quadrilateral ABCD be a parallelogram, if
AB = DC = 8 cm, AD = 4 cm and BC =4.4 cm?
View SolutionCan a quadrilateral ABCD be a parallelogram, if
`angleA = 70^@ and angleC = 65^@`?
View SolutionDraw a rough figure, of a quadrilateral that is not a parallelogram but has exactly two opposite angles of equal measure.

View SolutionThe measures of two adjacent angles of a parallelogram are in the ratio `3:2`. Find the measure of each of the angles of the parallelogram.
View SolutionTwo adjacent angles of a parallelogram have equal measure. Find the measure of each of the angles of the parallelogram.
View SolutionThe following figures GUNS and RUNS are parallelograms. Find x and y. (Lengths are in cm)
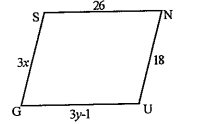
View SolutionThe following figures GUNS and RUNS are parallelograms. Find x and y. (Lengths are in cm)

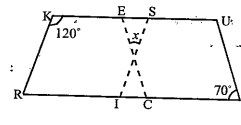
View SolutionIn the above figure both RISK and CLUE are parallelograms. Find the value of x.
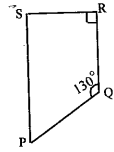
View SolutionExplain how this figure is a trapezium. Which of its two sides are parallel?

View SolutionFind `mangleC`.If AB||DC.

View SolutionFind the the measure of `angleP` and `angleS` if `barSP||barRQ`
(If you find `mangleR`, is there more than one method to find `mangleP`?)
View SolutionState whether True or False.
All rectangle are squares
View SolutionState whether True or False.
All rhombuses are parallelograms
View SolutionState whether True or False.
All squares are rhombuses and also rectangles
View SolutionState whether True or False.
All squares are not parallelograms
View SolutionState whether True or False.
All kites are rhombuses
View SolutionState whether True or False.
All rhombuses are kites
View SolutionState whether True or False.
All parallelograms are trapeziums
View SolutionState whether True or False.
All squares are trapeziums.
View SolutionIdentify all the quadrilaterals that have.
four sides of equal length
View SolutionIdentify all the quadrilaterals that have.
four right angles
View SolutionExplain how a square is.
a quadrilateral
View SolutionExplain how a square is.
a parallelogram
View SolutionExplain how a square is.
a rhombus
View SolutionExplain how a square is.
a rectangle
View SolutionName the quadrilaterals whose diagonals.
bisect each other
View SolutionName the quadrilaterals whose diagonals.
are perpendicular bisectors of each other
View SolutionName the quadrilaterals whose diagonals.
are equal
View SolutionExplain why a rectangle is a convex quadrilateral.
View SolutionABC is a right-angled triangle and O is the mid point of the side opposite to the right angle. Explain who O is equidistant from A,B and C. (The dotted lines are drawn additionally to help you.)
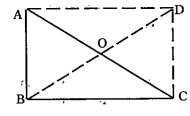
View SolutionTake any quadrilateral, say ABCD , Divide it into two triangles, by drawing a diagonal. You get six angles 1,2,3,4,5 and 6. Use the angle sum property of a triangle and argue how the sum of the measures of and amount to `180^@ + 180^@ = 360^@`.

View SolutionTake four congruent card-board copies of any quadrilateral ABCD, with angles as shown in the figures. Arrange the copies as shown in the figure, where angles `angle1, angle2,angle3,angle4` meet at a point. What can you say about the sum of the angles `angle1, angle2,angle3 and angle4`.
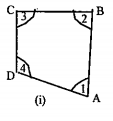
View SolutionTake four congruent card-board copies of any quadrilateral ABCD, with angles as shown in the figures. Arrange the copies as shown in the figure, where angles `angle1, angle2,angle3,angle4` meet at a point. What can you say about the sum of the angles `angle1, angle2,angle3 and angle4`.
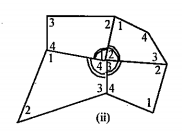
View SolutionConsider a concave quadrilateral ABCD, Split it into two triangles and find the sum of the interior angles.
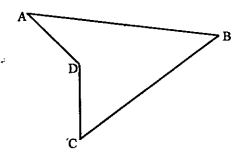
View SolutionTake a regular hexagon.
What is the sum of the measures of its exterior angles x,y,z,p,q,r?
View SolutionTake a regular hexagon.
Is x=y=z=p=q=r where x,y,z,p,q,r are exterior angles? Why?
View SolutionWhat is the measure of each exterior angle?
View SolutionWhat is the measure of each interior angle?
View SolutionDraw a rough figure, of a quadrilateral that is not a parallelogram but has exactly two opposite angles of equal measure.

View SolutionA mason has made a concrete slab. He needs it to be rectangular. In what different ways can he make sure that it is rectangular?
View SolutionA square was defined as a rectangle with all sides equal. Can we define it as rhombus with equal angles? Explore this idea.
View SolutionCan a trapezium have all angles equal? Can it have all sides equal? Explain.
View Solution
EXAMPLE questions and complete solutions for chapter Understanding Quadrilaterals. of ASHOK PUBLICATION ASSAM of Class 8