Complete Solutions to EXAMPLE of chapter Algebraic Expressions and Identities of Class 8 book with complete answers and questions
| Class 8 | MATHS |
| Chapter | Algebraic Expressions and Identities |
| ASHOK PUBLICATION ASSAM | EXAMPLE |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
Identify the terms, their coefficients for each of the following expressions.
`5xyz^2 - 3zy`
View SolutionIdentify the terms, their coefficients for each of the following expressions.
`1 + x + x^2`
View SolutionIdentify the terms, their coefficients for each of the following expressions.
`4x^2y^2 - 4x^2y^2z^2`
View SolutionIdentify the terms, their coefficients for each of the following expressions.
`3-pq+qr-rp`
View SolutionIdentify the terms, their coefficients for each of the following expressions.
`frac(x)(2) + frac(y)(2) - xy`
View SolutionIdentify the terms, their coefficients for each of the following expressions.
`0.3a - 0.6ab + 0.5b`
View SolutionClassify the following polynomials monomials, binomials, tribomials. Which polynomials do not fit in any of these three categories?

View SolutionAdd the following:
ab-bc, bc-ca, ca-ab
View SolutionAdd the following:
a-b+ab, b-c+bc, c-a + ac
View SolutionAdd the following:
`2p^2q^2 - 3pq + 4, 5+ 7 pq - 3p^2 q^2`
View SolutionAdd the following: l2 + m2, m2 + n2, n2 + l2, 2lm + 2mn + 2nl
View SolutionSubtract 4a - 7ab + 3b + 12 from 12a - 9ab + 5b -3
View SolutionSubtract 3xy + 5yz- 7zx from 5xy - 2yz -2zx + 10xyz
View SolutionSubtract `4p^2 q - 3pq + 5 pq^2 - 8p + 7q - 10` from `18-3p - 11 + 5pq - 2pq^2 + 5p^2 q`
View SolutionFind the product of the following pairs of monomials.
4,7p
View SolutionFind the product of the following pairs of monomials.
-4p,7p
View SolutionFind the product of the following pairs of monomials.
-4p, 7pq
View SolutionFind the product of the following pairs of monomials.
`4p^3, -3p`
View SolutionFind the product of the following pairs of monomials.
4p,0
View SolutionFind the areas of rectangles with the following pairs of monomals as their lengths and breadths respectively.
`(p,q), (10m,5n), (20x^2,5y^2), (4x,3x^2), (3mn, 4np)`
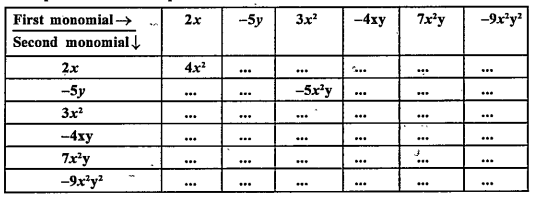
View SolutionComplete the table of products.
View SolutionObtain the volume of rectangular boxes with the following length, breadth and height respectively.
`5a, 3a^2, 7a^4`
View SolutionObtain the volume of rectangular boxes with the following length, breadth and height respectively.
`2p, 4q, 8r`
View SolutionObtain the volume of rectangular boxes with the following length, breadth and height respectively.
`xy,2x^2y,2xy^2`
View SolutionObtain the volume of rectangular boxes with the following length, breadth and height respectively.
a, 2b,3c
View SolutionObtain the product of
`xy,yz, zx`
View SolutionObtain the product of
`a, -a^2,a^3`
View SolutionObtain the product of
`2,4y,8y^2,16y^3`
View SolutionObtain the product of
`a,2b,3c,6abc`
View SolutionObtain the product of
`m, -mn, mnp`
View SolutionCarry out the multiplication of the expressions in each of the following pair.
4p,q+r
View SolutionCarry out the multiplication of the expressions in each of the following pair.
ab,a-b
View SolutionCarry out the multiplication of the expressions in each of the following pair.
`a+b,7a^2b^2`
View SolutionCarry out the multiplication of the expressions in each of the following pair.
`a^2-9,4a`
View SolutionCarry out the multiplication of the expressions in each of the following pair.
pq + qr + rp,0
View SolutionComplete the table.

View SolutionFind the product.
`(a^2)xx(2a^22)`x (4a^26)`
View SolutionFind the product.
`(frac(2)(3) xy) xx (frac(-9)(10) x^2 y^2)`
View SolutionFind the product.
`(-frac(10)(3)pq^3)) xx (frac(6)(5) p^3q))`
View SolutionFind the product.
`x xx x^2 xx x^3 xx x^4`
View SolutionSimplify 3 x (4x-5) +3 and find its values for
`x = frac(1)(2)`
View SolutionSimplify `a(a^2 + a+1) +5` and find its value for
a = 0
View SolutionSimplify `a(a^2 + a+1) +5` and find its value for
a=1
View SolutionSimplify `a(a^2 + a+1) +5` and find its value for
a = -1
View SolutionAdd : p(p-q),q(q-r) and (r-p)
View SolutionAdd : 2x(z-x-y) and 2y(z-y-x)
View SolutionSubtract : 3l(l - 4m + 5n) from 4l(10n - 3m + 2l)
View SolutionSubtract : 3a(a+b+c)-2b(a-b+c) from 4c(-a + b +c)
View SolutionMultiply the binomials.
(2x+5) and (4x -3)
View SolutionMultiply the binomials.
(y-8) and (3y -4)
View SolutionMultiply the binomials.
(2.5l - 0.5m) and (2.5l + 0.5m)
View SolutionMultiply the binomials.
(a+3b) and (x + 5)
View SolutionMultiply the binomials.
`(2pq + 3q^2) and (3pq-2q^2)`
View SolutionMultiply the binomials.
`(frac(3)(4) a^2 + 3b^2) and 4(a^2 -frac(2)(3) b^2)`
View SolutionFind the product:
(5-2x)(3+x)
View SolutionFind the product:
(x + 7y) (7x-y)
View SolutionFind the product:
`(a^2 + b) (a + b^2)`
View SolutionFind the product:
`(p^2 -q^2) (2p + q)`
View SolutionSimplify.
`(x^2 -5) (x+5) + 25`
View SolutionSimplify.
`(a^2 +5) (b^3 + 3) + 5`
View SolutionSimplify.
`(t + s^2) (t^2 -s)`
View SolutionSimplify.
(a+b)(c-d) + (a-b)(c+d) +2 (ac + bd)
View SolutionSimplify.
`(x + y)(2x + y) + (x + 2y)(x-y)`
View SolutionSimplify.
`(x+y)(x^2-xy + y^2)`
View SolutionSimplify.
`(1.5x -4y)(1.5x +4y +3) -4.5x + 12y`
View SolutionSimplify.
`(a+b+c) (a+b+c)`
View SolutionUse a suitable identity to get each of the following products
`(x+3)(x+3)`
View SolutionUse a suitable identity to get each of the following products
`(2y+5)(2y+5)`
View SolutionUse a suitable identity to get each of the following products
`(2a -7) (2a - 7)`
View SolutionUse a suitable identity to get each of the following products
`(3a -frac(1)(2))(3a -frac(1)(2))`
View SolutionUse a suitable identity to get each of the following products
`(1.1m-0.4)(1.1m + 0.4)`
View SolutionUse a suitable identity to get each of the following products
`(a^2 + b^2)(-a^2 + b^2)`
View SolutionUse a suitable identity to get each of the following products
`(6x -7) (6x + 7)`
View SolutionUse a suitable identity to get each of the following products
`(-a+c)(-a+c)`
View SolutionUse a suitable identity to get each of the following products
`(frac(x)(2) + frac(3y)(4))`
`(frac(x)(2) + frac(3y)(4))`
View SolutionUse a suitable identity to get each of the following products
`(7a-9b)(7a-9b)`
View SolutionUse the identity `(x+a)(x+b) =x^2 + (a+b)x + ab` to find the following products.
`(x+3)(x+7)`
View SolutionUse the identity `(x+a)(x+b) =x^2 + (a+b)x + ab` to find the following products.
`(4x+5)(4x+1)`
View SolutionUse the identity `(x+a)(x+b) =x^2 + (a+b)x + ab` to find the following products.
`(4x -5)(4x-1)`
View SolutionUse the identity `(x+a)(x+b) =x^2 + (a+b)x + ab` to find the following products.
`(4x + 5) (4x -1)`
View SolutionUse the identity `(x+a)(x+b) =x^2 + (a+b)x + ab` to find the following products.
`(2x+5y)(2x + 3y)`
View SolutionUse the identity `(x+a)(x+b) =x^2 + (a+b)x + ab` to find the following products.
`(2a^2 +9) (2a^2 + 5)`
View SolutionUse the identity `(x+a)(x+b) =x^2 + (a+b)x + ab` to find the following products.
`(xyz -4) (xyz -2)`
View SolutionFind the following squares by using the identities.
`(b-7)^2`
View SolutionFind the following squares by using the identities.
`(xy+ 3z)^2`
View SolutionFind the following squares by using the identities.
`(6x^2 - 5y)^2`
View SolutionFind the following squares by using the identities.
`(frac(2)(3)m + frac(3)(2) n)^2`
View SolutionFind the following squares by using the identities.
`(0.4p - 0.4q)^2`
View SolutionFind the following squares by using the identities.
`(2xy + 5y)^2`
View SolutionSimplify:
`(a^2 - b^2)^2`
View SolutionSimplify:
`(3x+5)^2 - (2x-5)^2`
View SolutionSimplify:
`(7m - 8n)^2 + (7m + 8n)^2`
View SolutionSimplify:
`(4m + 5n)^2 + (5m + 4n)^2`
View SolutionSimplify:
`(2.5 p - 1.5q)^2 - (1.5 p - 2.5 q)^2`
View SolutionSimplify:
`(ab+bc)^2 - 2ab^2c`
View SolutionSimplify:
`(m^2 - n^2m)^2 + 2m^3n^2`
View SolutionShow that:
`(3x + 7)^2 - 84x = (3x - 7)^2`
View SolutionShow that:
`(9p - 5q)^2 + 180 pq = (9p+ 5q)^2`
View SolutionShow that:
`(frac(4)(3)m -frac(3)(4)n)^2 + 2mn = frac(16)(9) m^2 + frac(9)(16)n^2`
View SolutionShow that:
`(4pq + 3q)^2 - (4pq - 3q)^2 = 48 pq^2`
View Solution
EXAMPLE questions and complete solutions for chapter Algebraic Expressions and Identities of ASHOK PUBLICATION ASSAM of Class 8