Complete Solutions to OLYMPAID/HOTS CORNER of chapter UNDERSTANDING QUADRILATERALS of Class 8 book with complete answers and questions
| Class 8 | MATHS |
| Chapter | UNDERSTANDING QUADRILATERALS |
| MTG IIT JEE FOUNDATION | OLYMPAID/HOTS CORNER |
| Number Of Questions | 11 |
| Academic Year | 2023-24 |
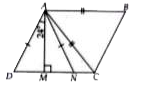
If ABCD is a parallelogram `DeltaADN` and `DeltaABC` are isosceles triangles, then find `/_BAC`.
View SolutionIn the given figure DO and CO are the bisectors of `/_ADC` and `/_BCD` respectively. If `/_ADC=/_BCD=60^(@)` and `/_DAB=100^(@)` find
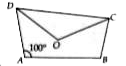
`/_DOC` and `/_ABC`
View SolutionThe diagonals of a rectangle `A B C D` meet at `Odot` If `/_B O C=44^0,` find `/_O A Ddot`
View SolutionABCD is a square of area of 4 square units which is divided into 4 non overlapping triangles as shown in figure, then sum of perimieters of the triangles so formed is

View SolutionMatch the following

View SolutionIn the given figure (not drawn to scale), ABCD is a parallelogram and GBEF is a rectangle. Find
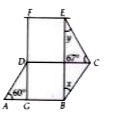
(i) x (ii) y
View SolutionThe measures of the five angles of a hexagon are equal and the sixth angle measures `100^(@)`, then the measure of each of the five angles is
View SolutionIf the given figure is made up of 3 identical regular polygons, then find
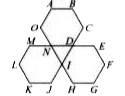
(i) `/_ABC` (ii) `/_DIN`
View SolutionSides AB and CD of a quadrilateral ABCD are extended as shown in the figure Then a+b is equal to
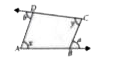
View SolutionIn the given figure ABCD is a parallelogram. Then the values of x and y respectively are

View Solutionin the figure, `X` is a point in the interior of square `ABCD. AXYZ` is also a square. If `DY = 3 cm and AZ = 2 cm.` Then `BY =`
View Solution
OLYMPAID/HOTS CORNER questions and complete solutions for chapter UNDERSTANDING QUADRILATERALS of MTG IIT JEE FOUNDATION of Class 8
All Exercises from MTG IIT JEE FOUNDATION Class 8 MATHS UNDERSTANDING QUADRILATERALS
- EXERCISE(MULTIPLE CHOICE QUESTION LEVEL-1)
- EXERCISE(MULTIPLE CHOICE QUESTION LEVEL-2 ASSERTION AND REASON TYPE)
- EXERCISE(MULTIPLE CHOICE QUESTION LEVEL-2 COMPREHENSION TYPE)
- EXERCISE(MULTIPLE CHOICE QUESTION LEVEL-2 MATCH THE FOLLOWING)
- EXERCISE(MULTIPLE CHOICE QUESTION LEVEL-2 SUBJECTIVE PROBLEMS)
- EXERCISE(MULTIPLE CHOICE QUESTION LEVEL-2)
- ILLUSTRATIONS
- NCERT SECTION (EXERCISE 3.1)
- NCERT SECTION (EXERCISE 3.2)
- NCERT SECTION (EXERCISE 3.3)
- NCERT SECTION (EXERCISE 3.4)
- OLYMPAID/HOTS CORNER
- SOLVED EXAMPLES