Complete Solutions to Example of chapter चतुर्भुजों को समझना of Class 8 book with complete answers and questions
| Class 8 | MATHS |
| Chapter | चतुर्भुजों को समझना |
| SHIVLAAL PUBLICATION | Example |
| Number Of Questions | 14 |
| Academic Year | 2023-24 |
निम्न आकृतियों का सुमेलन कीजिए (ध्यान रखिए! एक आकृति का एक से अधिक आकृतियों से सुमेलन हो सकता है:
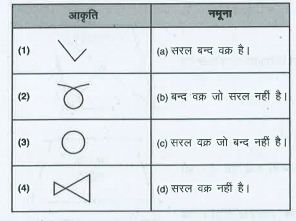 अपने मित्रों से इस मिलान की तुलना कीजिए। क्या वे सहमत हैं?
अपने मित्रों से इस मिलान की तुलना कीजिए। क्या वे सहमत हैं?
View Solutionकुछ और बहुभुजों के उदाहरण देने का प्रयास कीजिए तथा कुछ और ऐसे उदाहरण दीजिए जो बहुभुज न हो ।
View Solutionसत्य `(T)` या असत्य`(F)` कहिए :
`(a)` आयत का प्रत्येक कोण समकोण होता है |
`(b)` आयत की सम्मुख भुजाओं की लंबाई बराबर होती है |
`(c)` वर्ग के विकर्ण एक दूसरे पर लंब होते हैं |
`(d)` समचतुर्भुज की सभी भुजाएँ बराबर लंबाई की होती हैं |
`(e)` समांतर चतुर्भुज की सभी भुजाएँ बराबर लंबाई की होती है |
`(f)` समलंब की सम्मुख भुजाएँ समांतर होती है |
View Solutionक्या आप संलग्न आकृतियों में प्रत्येक विकर्ण का नाम दे सकते हैं? क्या PQ एक विकर्ण है? LN के बारे में आप क्या कह सकते हैं?
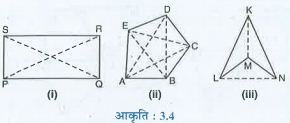
View Solutionसमांतर चतुर्भुज का एक कोण दूसरे कोण का दुगुना है। चारों कोणों का मान ज्ञात कीजिए
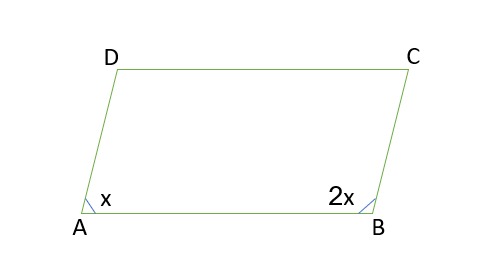
View Solutionक्या आप बता सकते हैं कि इस प्रकार के बहुभुज एक-दूसरे से अलग क्यों है? जो बहुभुज उत्सल होते हैं उनके विकर्णो का कोई भी भाग बहिभाग में नहीं होता है। क्या यह अवतल बहुभुजों के लिए भी सत्य होता है? दी गई आकृतियों का अध्ययन कीजिए। तदुपरान्त अपने शब्दों में उत्तल बहुभुज तथा अवतल बहुभुज समझाने का प्रयास कीजिए। प्रत्येक प्रकार की दो आकृतियाँ बनाइए।
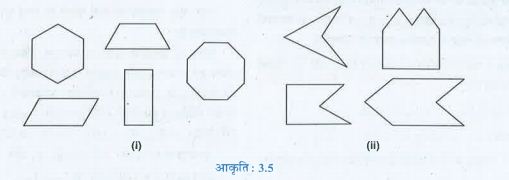
View Solutionक्या एक आयत एक समबहुभुज है?
View Solutionक्या एक समबाहु त्रिभुज समबहभज है? क्यों?
View Solutionक्या आपने किसी ऐसे चतुर्भुज के बारे में पड़ा है जो समभुज तो हो परन्तु समकोणिक न हो?
View Solutionक्या कोई ऐसा त्रिभुज है जो समभुज तो हो परन्तु समकोणिक न हो?
View Solutionकोई एक चतुर्भुज, माना ABCD लीजिए
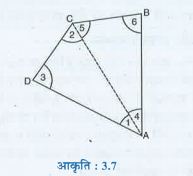 (संलग्न चित्र 3.7)। एक विकर्ण खींचकर इसे दो त्रिभुजों में बाँटिए। आप छः कोण 1,2,3,4,5 और 6 प्राप्त करते हैं। त्रिभुज के कोण -योग वाले गुण-धर्म का उपयोग कीजिये और तर्क कीजिये की कैसे `/_A, /_B, /_C` तथा `/_D` के मापों का `180^@ + 180^@=360^@` योगफल हो जाता है.
(संलग्न चित्र 3.7)। एक विकर्ण खींचकर इसे दो त्रिभुजों में बाँटिए। आप छः कोण 1,2,3,4,5 और 6 प्राप्त करते हैं। त्रिभुज के कोण -योग वाले गुण-धर्म का उपयोग कीजिये और तर्क कीजिये की कैसे `/_A, /_B, /_C` तथा `/_D` के मापों का `180^@ + 180^@=360^@` योगफल हो जाता है.
View Solutionकिसी चतुर्भुज ABCD, की गत्ते वाली चार सर्वांगसम प्रतिलिपियाँ लीजिए जिनके कोण दर्शाए गए हैं। [आकृति 3.8 (i))। इन प्रतिलिपियों को इस प्रकार से व्यवस्थित कीजिए जिसमें `/_1, /_2, /_3, /_4` एक ही बिन्दु पर मिलें जैसा कि आकृति 3.8 (10) में है।
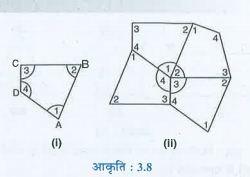 आप `/_1, /_2, /_3` तथा `/_4` के योगफल के बारे में क्या कह सकते है?
आप `/_1, /_2, /_3` तथा `/_4` के योगफल के बारे में क्या कह सकते है?
View Solutionचतुर्भुज ABCD पर पुनः विचार कीजिये (चित्र 3 .9 )। माना इसके अभ्यंतर में कोई बिंदु P स्तिथ है। P को शीशो A,B,C तथा D से जोड़िये। आकृति में `/_\PAB` पर विचार कीजिये। हम देखते है की `x=180^@ -m/_2 – m/_3`, इसी प्रकार से `/_\PBC`, से `y=180^@ -m/_4 – m/_5`, `/_\PCD`, से `z=180^@ -m/_6 – m/_7`, और`/_\PDA`, से `w=180^@ -m/_8 – m/_1`.
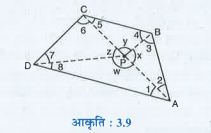 इसका उपयोग करके कुल माप ` m/_1 +m/_2_ + … + m/_8` ज्ञान कीजिये क्या यह आपको परिणाम तक पहुँचाने में सहायता करता है? यदि रखिए `/_x + /_y + /_z + /_w = 360^@` है।
इसका उपयोग करके कुल माप ` m/_1 +m/_2_ + … + m/_8` ज्ञान कीजिये क्या यह आपको परिणाम तक पहुँचाने में सहायता करता है? यदि रखिए `/_x + /_y + /_z + /_w = 360^@` है।
View Solutionयदि चतुर्भुज उत्तल नहीं होते तो क्या होता? चतुर्भुज ABCD पर विचार कीजिए।
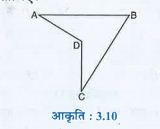
इसे जो त्रिभुजों में बांटिए और अंत, कोणों का योगफल गुना कीजिये (चित्र : 3.10) ।
View Solution
Example questions and complete solutions for chapter चतुर्भुजों को समझना of SHIVLAAL PUBLICATION of Class 8