Complete Solutions to साधित उदाहरण of chapter त्रिभुजों की सर्वागसमता एवं त्रिभुजों में असमानता of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | त्रिभुजों की सर्वागसमता एवं त्रिभुजों में असमानता |
| ALOK BHARTI PUBLICATION | साधित उदाहरण |
| Number Of Questions | 21 |
| Academic Year | 2023-24 |
`trianglePQR` में PQ = PR और `angleQ = 2angleP` तो त्रिभुज के प्रत्येक कोण की माप निकालें।
View Solutionसिद्ध करें कि समबाहु त्रिभज के प्रत्येक कोण की माप `60^@` होती है।
View Solutionयदि किसी त्रिभुज के शीर्ष बिन्दु से गुजरने वाली सरल रेखा आधार का लम्ब समद्विभाजक हो तो सिद्ध करें कि वह त्रिभुज समद्विबाहु त्रिभुज होगा।
View Solutionयदि किसी त्रिभुज के शीर्ष कोण का समद्विभाजक आधार को भी समद्विभाजित करे तो सिद्ध करें कि वह त्रिभुज एक समद्विबाहु त्रिभुज होगा।
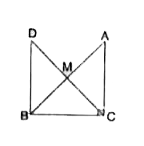
View Solutionसमकोण `triangleABC` में `angleC = 90^@` एवं M, AB का मध्य बिन्दु है। बिन्दु C को M से मिलाया गया एवं इसे विन्दु D तक इस प्रकार बढ़ाया गया कि CM = DM. बिन्दु D को B से मिलाया गया।
सिद्ध करें कि
(i)`triangleAMC cong triangleBMD` , (ii)`angleDBC=90^@` , (iii)`triangleDBC cong triangleACB` एवं `CM=1/2AB`
View SolutionABC एक समद्विबाहु त्रिभुज है जिसमें AB = AC है। BA भुजा को D बिन्दु तक इस प्रकार बढ़ाया कि AD = AB, दिखायें कि `angleBCD=90^@`
View SolutionBE एवं CF, `triangleABC` के दो समान शीर्षलम्ब हैं। R.H.S. सर्वांगसमता का प्रयोग करते हुए सिद्ध करें कि `triangleABC` एक समद्विबाहु त्रिभुज होगा।
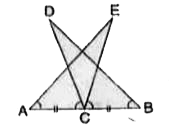
View Solutionबगल की आकृति में AC=BC , `angleDCA=angleECB` तथा `angleDBC=angleEAC` है।
सिद्ध करें कि `triangleDBC cong triangleEAC`
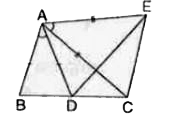
View Solutionदी गई आकृति में AC = AE, AB =AD और `angleBAD=angleEAC`
सिद्ध करें कि BC=DE
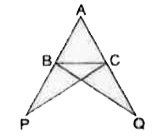
View Solutionनीचे दी गई आकृति में ABC एक समद्विबाहु त्रिभुज है जिसमें AB = AC है । AB एवं AC को क्रमश: P एवं Q बिन्दु तक इस प्रकार बढ़ाया गया है कि AP = AQ, सिद्ध करें कि PC=BQ
View SolutionABC एक त्रिभुज है जिसमें `angleB = 2angleC, BC` भुजा पर एक बिन्दु D इस प्रकार है कि AB = CD तथा AD, `angleBAC` को समद्विभुज करता है। सिद्ध करें कि `angleBAC=72^@` .
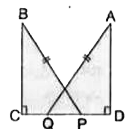
View Solutionदी गई आकृति में `AD bot CD` एवं `BC bot CD` है। यदि AQ = BP एवं DP = CQ हो तो सिद्ध करें कि `angleDAQ=angleCBP`
View Solutionकिसी समकोण त्रिभुज में एक न्यूनकोण दूसरे का दुगुना है । सिद्ध करें कि इस समकोण त्रिभुज का कर्ण सबसे छोटी भुजा का दुगुना है।
View Solutionसिद्ध करें कि किसी त्रिभुज की दो भुजाओं का योगफल उसकी तीसरी भुजा की माध्यिका के दुगुने से बड़ा होता है
View Solution`trianglePQR` के अभ्यंतर में एक बिन्दु O है सिद्ध करें कि OQ+OR `lt` PQ + PR
View Solutionसिद्ध करें कि किसी समकोण त्रिभुज में कर्ण उसकी सबसे बड़ी भुजा होती है।
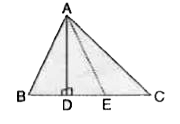
View Solutionदी गई आकृति में `triangleABC` में `AD bot BC` एवं `DC gt DB` तथा DE=DB तो सिद्ध करे कि AC `gt` AB
View Solution`triangleABC` में `AC gt AB` एवं AD, `angleA` का समद्विभाजक है। सिद्ध करें कि `angleADC gt angleADB`
View Solutionदी गयी आकृति में `triangleABC` की भुजाएँ AB तथा AC क्रमश: P एवं Q तक बढ़ायी गयी हैं एवं `anglePBC lt angleQCB` है। सिद्ध करें कि AC `gt` AB
View Solution`trianglePQR` की भुजा QR पर एक बिन्दु T है एवं कोई एक बिन्दु S इस प्रकार है कि RT = ST, सिद्ध करें कि `PQ + PR gt QS`
View Solutionसिद्ध करें कि किसी त्रिभुज की तीनों भुजाओं का योगफल उसकी तीनों माध्यिकाओं के योगफल से बड़ा होता है।
View Solution
साधित उदाहरण questions and complete solutions for chapter त्रिभुजों की सर्वागसमता एवं त्रिभुजों में असमानता of ALOK BHARATI MATHS (HINDI) of Class 9
All Exercises from ALOK BHARTI PUBLICATION Class 9 MATHS त्रिभुजों की सर्वागसमता एवं त्रिभुजों में असमानता
- प्रश्नावली (Exercise) 10
- प्रश्नावली (Exercise) 11
- प्रश्नावली (Exercise) 12
- प्रश्नावली (Exercise) 13
- प्रश्नावली (Exercise) 14
- प्रश्नावली (Exercise) 15
- प्रश्नावली (Exercise) 16
- प्रश्नावली (Exercise) 17
- प्रश्नावली (Exercise) 18
- प्रश्नावली (Exercise) 19
- प्रश्नावली (Exercise) 20
- प्रश्नावली (Exercise) 21
- प्रश्नावली (Exercise) 22
- प्रश्नावली (Exercise) 23
- प्रश्नावली (Exercise) 25
- प्रश्नावली (Exercise) 26
- प्रश्नावली (Exercise) 27
- प्रश्नावली (Exercise) 28
- प्रश्नावली (Exercise) 29
- प्रश्नावली (Exercise) 30
- प्रश्नावली (Exercise) 31
- प्रश्नावली (Exercise) 35
- प्रश्नावली (Exercise) 36
- प्रश्नावली (Exercise) 39
- प्रश्नावली (Exercise) 41
- प्रश्नावली (Exercise) 42
- प्रश्नावली (Exercise) 43
- प्रश्नावली (Exercise) 45
- प्रश्नावली (Exercise) 9
- प्रश्नावली (Exercise) 9 (अतिलघु उत्तरीय प्रश्न )
- प्रश्नावली (Exercise) 9 (बहुविकल्पीय प्रश्न)
- साधित उदाहरण