Complete Solutions to EXERCISE 10.2 (प्रश्नावली) लघु उत्तरीय प्रश्न of chapter चतुर्भुज of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | चतुर्भुज |
| ALOK BHARTI PUBLICATION | EXERCISE 10.2 (प्रश्नावली) लघु उत्तरीय प्रश्न |
| Number Of Questions | 14 |
| Academic Year | 2023-24 |
यदि किसी समांतर चतुर्भुज का एक कोण अपने आसन्न कोण का दो-तिहाई है। इसके प्रत्येक कोण की माप बताएँ।
View Solution(a) समान्तर चतुर्भुज ABCD में `angle A = (2x + 25)`""^(@)`` एवं `angle B = (3x - 5)^@` हो तो `x` का मान बताएँ।
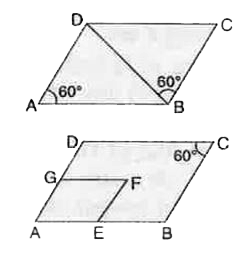
(b) दी गयी आकृति में समान्तर चतुर्भुज ABCD में `angle DAB = angle DBC = 60`""^(@)`` है।
(i) `angle CDB` (ii) `angle ADB` मान ज्ञात करें।
(c) दी गयी आकृति में ABCD एवं AEFG दो समांतर चतुर्भुज हैं। यदि `angle C = 60^@` हो तो (i) `angle F ` (ii) `angle AGF` की माप बताएँ।
View Solution(a) किसी समचतुर्भुज के विकर्णों की लम्बाई 12 सेमी एवं 16 सेमी हो तो इसके प्रत्येक भुजा की लम्बाई ज्ञात करें।
(b) किसी समचतुर्भुज के प्रत्येक भुजा की माप 10 सेमी एवं इसके एक विकर्ण की लम्बाई 16 सेमी है। इसके दूसरे विकर्ण की लम्बाई ज्ञात करें।
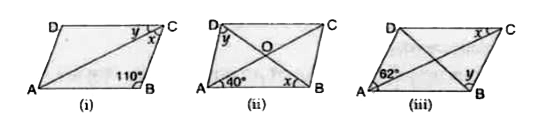
View Solutionनीचे दी गयी प्रत्येक आकृति में ABCD एक समचतुर्भुज है। प्रत्येक चित्र में `x` एवं `y` का मान ज्ञात करें।
View Solution(a) यदि किसी समांतर चतुर्भुज का एक कोण छोटे कोण के दुगुने से 30`""^(@)` कम है तो इसके प्रत्येक कोण की माप बताएँ।
(b) समान्तर चतुर्भुज ABCD की परिमाप 30 सेमी तथा AB की लम्बाई 9.5 सेमी है। BC की लम्बाई ज्ञात करें।
View Solutionदी गयी आकृति में ABCD एवं ADEF दो B समांतर चतुर्भुज है। यदि CA = AF तथा `angle ACD= 60^@` हो, तो `angle ECF` का मान ज्ञात करें।

View SolutionP, Q, R एवं S क्रमशः किसी समचतुर्भुज की भुजाओं AB, BC, CD एवं DA के मध्यबिन्दु हैं। सिद्ध करें कि PQRS एक आयत होगा।
View Solutionसामांतर चतुर्भुज ABCD में `angle A` एवं `angle C` के समद्विभाजक `DC` एवं `AB` से क्रमशः `P` एवं `Q` बिन्दुओं पर मिलते हैं। सिद्ध करें कि `APCQ` एक समांतर चतुर्भुज होगा।
View Solution`Delta ABC` की माध्यिका `AD`, बिन्दु `X` तक इस प्रकार बढ़ायी गयी है कि `AD = DX` है। सिद्ध करें कि `ABXC` एक समांतर चतुर्भुज होगा।
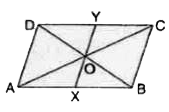
View Solutionदी गयी आकृति में समान्तर चतुर्भुज `ABCD` के विकर्ण एक-दूसरे को बिन्दु-O पर प्रतिच्छेद करते हैं। एक सरल रेखा `XOY , AB` एवं `CD` को क्रमशः बिन्दुओं `X` एवं `Y` पर काटती है। सिद्ध करें कि `OX = OY`
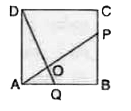
View Solutionदी गयी आकृति में `ABCD` एक वर्ग है। `A` को `BC` पर स्थित किसी बिन्दु P से तथा D को AB पर स्थित किसी बिन्दु `Q` से मिलाया गया है। यदि `AP = DQ` हो तो सिद्ध करें कि `AP bot DQ` है।
View Solutionसमांतर चतुर्भुज ABCD की भुजाएँ AB तथा AD क्रमश: बिन्दुओं E एवं F तक इस प्रकार बढ़ायी गयी हैं कि AB = BE एवं AD = DF है। साबित करें कि ECF एक सरल रेखा होगी।
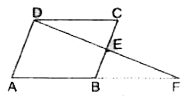
View Solutionदी गयी आकृति में ABCD एक समांतर चतुर्भुज है तथा E, BC का मध्यबिन्दु है। यदि DE एवं AB को आगे की ओर बढ़ाने पर बिन्दु F पर मिलती हो तो सिद्ध करें कि AF = 2AB होगा।
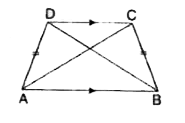
View Solutionएक समलम्ब `square ABCD` में, `AB ||DC` एवं `AD = BC` है। सिद्ध करें कि `DeltaABC ~= Delta BAD`
View Solution
EXERCISE 10.2 (प्रश्नावली) लघु उत्तरीय प्रश्न questions and complete solutions for chapter चतुर्भुज of ALOK BHARATI MATHS (HINDI) of Class 9
All Exercises from ALOK BHARTI PUBLICATION Class 9 MATHS चतुर्भुज
- EXERCISE 10.1 (प्रश्नावली) अतिलघु उत्तरीय प्रश्न (रिक्त स्थानों की पूर्ति करें।)
- EXERCISE 10.1 (प्रश्नावली) अतिलघु उत्तरीय प्रश्न (सही विकल्प चुनें)
- EXERCISE 10.1 (प्रश्नावली) लघु उत्तरीय प्रश्न
- EXERCISE 10.2 (प्रश्नावली) अतिलघु उत्तरीय प्रश्न
- EXERCISE 10.2 (प्रश्नावली) अतिलघु उत्तरीय प्रश्न (बहुविकल्पीय प्रश्न)
- EXERCISE 10.2 (प्रश्नावली) अतिलघु उत्तरीय प्रश्न (रिक्त स्थानों की पूर्ति करें।)
- EXERCISE 10.2 (प्रश्नावली) लघु उत्तरीय प्रश्न
- EXERCISE 10.3 (प्रश्नावली) अतिलघु उत्तरीय प्रश्न
- EXERCISE 10.3 (प्रश्नावली) अतिलघु उत्तरीय प्रश्न (रिक्त स्थानों की पूर्ति करें।)
- EXERCISE 10.3 (प्रश्नावली) लघु उत्तरीय प्रश्न
- SOLVED EXAMPLE (साधित उदाहरण)