Complete Solutions to उदाहरण of chapter क्षेत्रफल of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | क्षेत्रफल |
| ALOK BHARTI PUBLICATION | उदाहरण |
| Number Of Questions | 21 |
| Academic Year | 2023-24 |
ABCD एक समान्तर चतुर्भुज है, `AE _|_` DC और `CF _|_ AD` है। यदि AB= 16 सेमी, AE = 8 सेमी और CF = 10 सेमी, तो AD ज्ञात करें।

View SolutionP और Q समान्तर चतुर्भुज ABCD की भुजाओं DC और AD पर स्थित दो बिंदु हैं सिद्ध करें कि ar`(Delta APB ) = `ar `(Delta BQC )`
View Solutionयदि E,F,G,H क्रमशः समान्तर चतुर्भुज ABCD की भुजाओं के मध्य बिंदु हैं, तो दिखाएँ कि
`ar(squareEFGH) = ( 1)/(2) ar( squareABCD)` है।
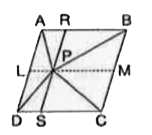
View Solutionदी गयी आकृति में, P समान्तर चतुर्भज ABCD के अभ्यांतर में स्थित कोई बिंदु है। दर्शाएं कि
(i) `ar (Delta APB ) + ar (Delta PCD ) = (1)/(2)
(ar||^(g m)ABCD)`
(ii) `ar(Delta APD) + ar(Delta BPC ) = ar(Delta APB) + ar(Delta PCD) `
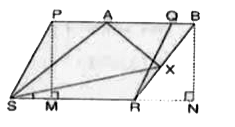
View Solutionदी गयी आकृति में PQRS एवं ABRS दो समान्तर चतुर्भुज हैं तथा X भुजा BR पर स्थित कोई बिंदु है। दर्शाइए कि
(i) `ar(||^(g m) PQRS) = ar ( ||^(g m) ABRS)`
(ii) `ar ( Delta AXS ) = ( 1)/(2) ar ( ||^(g m) PQRS) `
View Solutionसिद्ध करें कि किसी त्रिभुज की माध्यिका उसे समान क्षेत्रफल वाले दो त्रिभुजों में बाँटती है।
View Solutionएक किसान के पास समान्तर चतुर्भुज PQRS के रूप में एक खेत है। उसने RS पर स्थित कोई बिंदु A लिया और उसे P एवं Q से मिला दिया। खेत कितने भागों में विभाजित हो गया है ? इन भागों के आकार क्या है ? वह किसान खेत में गेहूँ और दालें बराबर -बराबर भागों में अलग-अलग बोना चाहता है। वह ऐसा कैसे करेगा ?
View SolutionPQRS एक समान्तर चतुर्भुज है। X एवं Y क्रमशः QR एवं SR के मध्यबिंदु हैं। सिद्ध करें कि
`ar ( Delta PXY) = ( 3)/( 8) ar(||^(g m) PQRS )`
View Solutionयदि `Delta ABC` की मध्यिकाएँ एक -दूसरे को G बिंदु पर परिच्छेद करें तो सिद्ध करें
`ar ( Delta AGB ) = ar (Delta BGC ) = ar( Delta AGC ) = ( 1)/( 3) ar ( Delta ABC )`
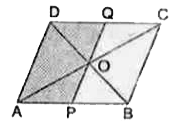
View Solutionदी गयी आकृति में ABCD एक समान्तर चतुर्भुज है। विकर्ण AC एवं BD एक-दूसरे को O बिंदु पर प्रतिच्छेद करते हैं। o बिंदु से होती हुई एक रेखा PQ खींची गयी है जो AB को P बिंदु तथा DC को Q बिंदु पर काटती है। सिद्ध करें कि
`ar (square APQD ) = ( 1)/(2) ar( ||^( g m ) ABCD )`
View Solution`Delta ABC` की माध्यिका AD पर स्थित E कोई बिंदु है। दर्शाइए कि `ar(Delta ABE ) = ar ( Delta ACE )`
View Solutionचतुर्भुज ABCD के विकर्ण AC एवं BD परस्पर बिंदु P पर परिच्छेद करते हैं। सिद्ध करें कि
`ar (Delta APB ) xx ar ( Delta CPD ) = ar ( Delta APD ) xx ar ( Delta BPC )`
View SolutionABCD एक समानांतर चतुर्भुज है और BC को किसी बिंदु Q तक इस प्रकार बढ़ाया गया कि AD =CQ है। यदि AQ भुजा DC को P पर प्रतिच्छेद करती है तो सिद्ध करें कि
`ar(Delta BPC ) = ar(Delta DPQ )`
View Solutionदी गयी आकृति में भुजा BC पर दो बिंदु D एवं E इस प्रकार स्थित है कि `BD =DE=EC`, सिद्ध करें कि
`ar(Delta ABD ) = ar ( Delta DE ) = ar ( Delta AEC )`
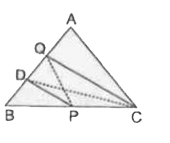
View Solutionदी गयी आकृति में बिंदु D,`Delta ABC` की भुजा AB का मध्यबिंदु है और P भुजा BC पर कोई बिंदु है। यदि `CQ || PD` हो तो सिद्ध करें कि
`ar( Delta BPQ ) = ( 1)/( 2) ar ( Delta ABC )`
View SolutionABC और ABD एक ही आधार AB पर बने दो त्रिभुज हैं। यदि रेखाखंड CD,AB से O बिंदु पर समद्विभाजित होता है तो दर्शाइए कि `ar(Delta ABC ) = ar ( Delta ABD )`
View SolutionD,E, और F क्रमशः `Delta ABC ` की भुजाओं BC,CA एवं AB के मध्य बिंदु हैं। दर्शाइए कि
(i) BDEF एक समान्तर चतुर्भुज है।
(ii) `ar(Delta DEF ) = ( 1)/(2) ar(Delta ABC )`
(iii) `ar( ||^(g m) BDEF ) = ( 1)/(2) ar ( Delta ABC )`
View Solutionमाना कि P,Q,R,S क्रमशः चतुर्भुज ABCD की भुजाओं AB,BC,CD एवं DA के मध्यबिंदु हैं दर्शाएँ कि
(i) PQRS एक समान्तर चतुर्भुज है।
(ii) `ar( ||^( g m ) PQRS) = ( 1)/(2) ar ( square ABCD )`
View SolutionABCD एक समतल चतुर्भुज है ,जिसमें AB `||` DC है AC के समान्तर खींची गयी एक रेखा AB को X पर तथा BC को Y पर प्रतिच्छेद करती है। सिद्ध करें कि
`ar( Delta ADX ) = ar (Delta ACY )`
View SolutionXY,`Delta ABC` की भुजा BC के समांतर एक रेखा है। यदि `BE || AC ` और `CF || AB` रेखा XY से क्रमशः E और F बिंदुओं पर मिलती है तो दर्शाइए कि
`ar( Delta ABE ) = ar ( Delta ACF)`
View Solutionएक आयत ABCD के अभ्यन्तर में स्थित एक बिंदु O से इसके शीर्षबिंदुओं A,B,C एवं D को मिलाया गया है। सिद्ध करें कि
`ar ( Delta AOD ) + ar ( Delta BOC ) = ar ( Delta AOB ) +ar(Delta COD )`
View Solution
उदाहरण questions and complete solutions for chapter क्षेत्रफल of ALOK BHARATI MATHS (HINDI) of Class 9