Complete Solutions to अभ्यास प्रश्न 12.1 of chapter त्रिभुजों की सर्वांगसमता of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | त्रिभुजों की सर्वांगसमता |
| BALAJI PUBLICATION | अभ्यास प्रश्न 12.1 |
| Number Of Questions | 11 |
| Academic Year | 2023-24 |
चित्र में वर्ग ABCD में एक बिंदु X है । AX पर एक वर्ग AXYZ बनाया जाता है ।
सिद्ध कीजिए किBX = DZ

View Solutionदिये गये चित्र में AD और BC परस्पर O पर प्रतिच्छेद करते है तो सिद्ध कीजिए :
(i)` AB = CD " तथा " AC = BD `
(ii) `angleBCD = angleCBA" तथा " angleDAC = angleADB`

View Solutionएक त्रिभुज ABC की माध्यिकाएँ BE और CF बराबर है । तो सिद्ध कीजिए कि त्रिभुज समद्विबाहु है ।
(संकेत : माध्यिकाओं का प्रतिच्छेद बिंदु इन्हें 2:1 के अनुपात में विभाजित करता है । )
View Solutionदिये गये चित्र में , एक वर्ग PQRS तथा SRT के समबाहु त्रिभुज है तो सिद्ध कीजिए
(i) PT = QT
(ii) ` angleQRT = 150^(@)`
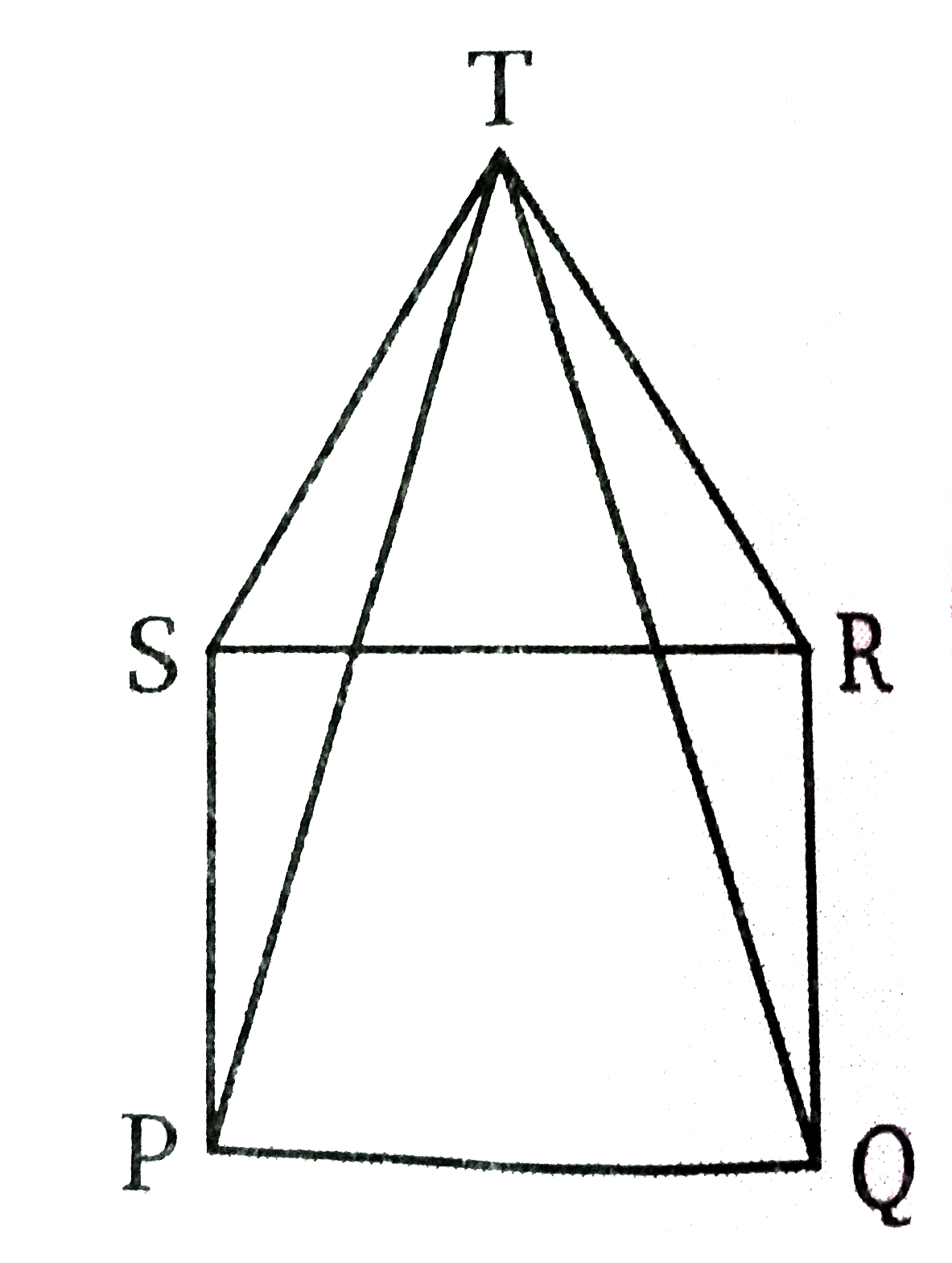
View SolutionABC एक समबाहु त्रिभुज है ,D कोई इसका अन्तः केंद्र है । DC पर एक समद्विबाहु त्रिभुज DEC खींचा गया है । (चित्र में दिखाये (CE=DC) अनुसार ) तो सिद्ध कीजिए कि `DeltaACE` तथा `DeltaBCD` सर्वांगसम है ।
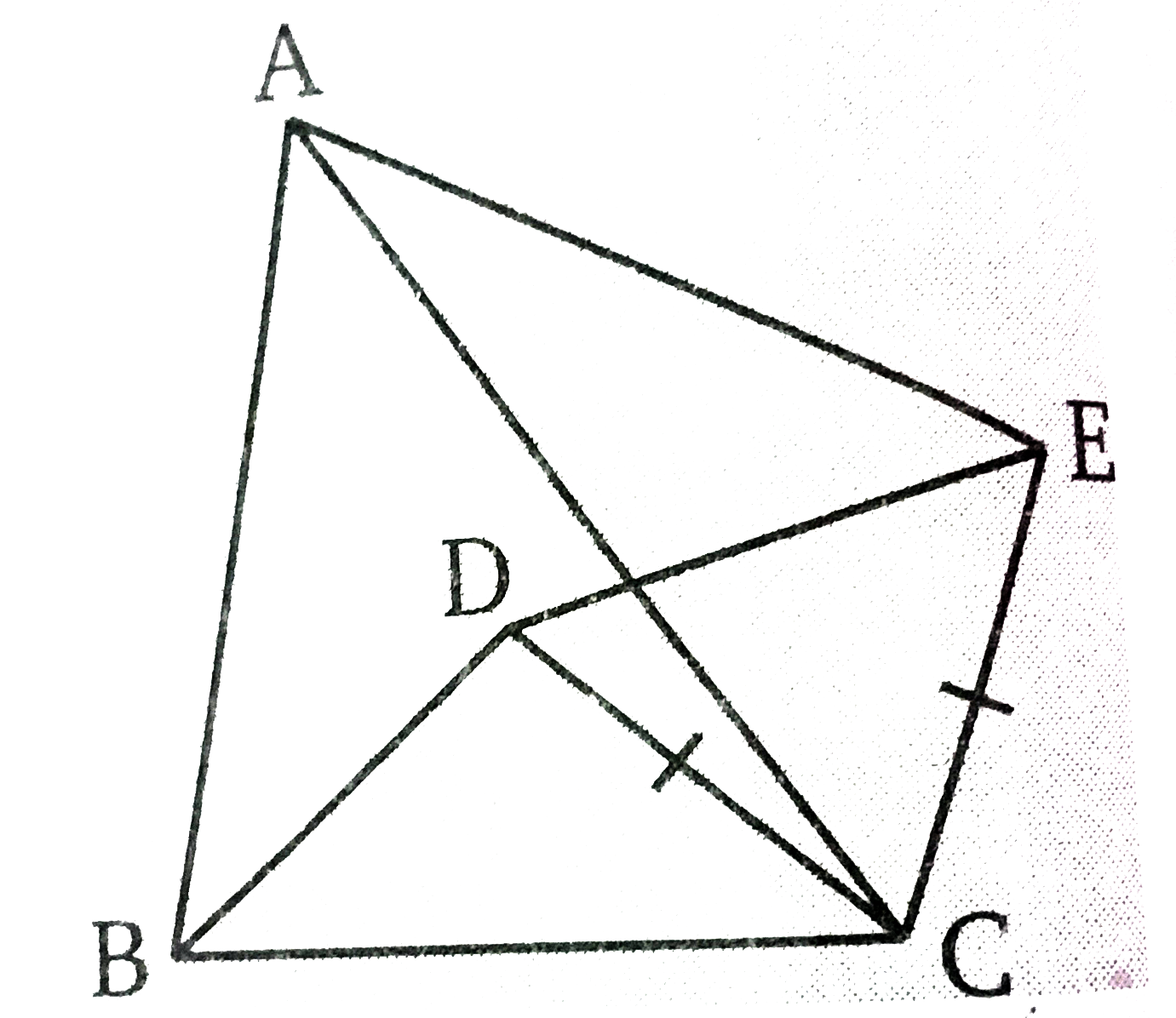
View Solutionभुजा AB = AC का एक समद्विबाहु त्रिभुज ABC है तथा `angleB" तथा "angleC` के समद्विभाजक परस्पर O पर प्रतिच्छेद करते है । तो सिद्ध कीजिए कि `BO = CO " तथा "AO, angleBAC` का समद्विभाजक है ।
View Solutionदिये गये चित्र में ,`BA bot AC" तथा "DE bot EF` इस प्रकार है कि `BA = DE" तथा " DF = BC` तो सिद्ध कीजिए कि AC = EF

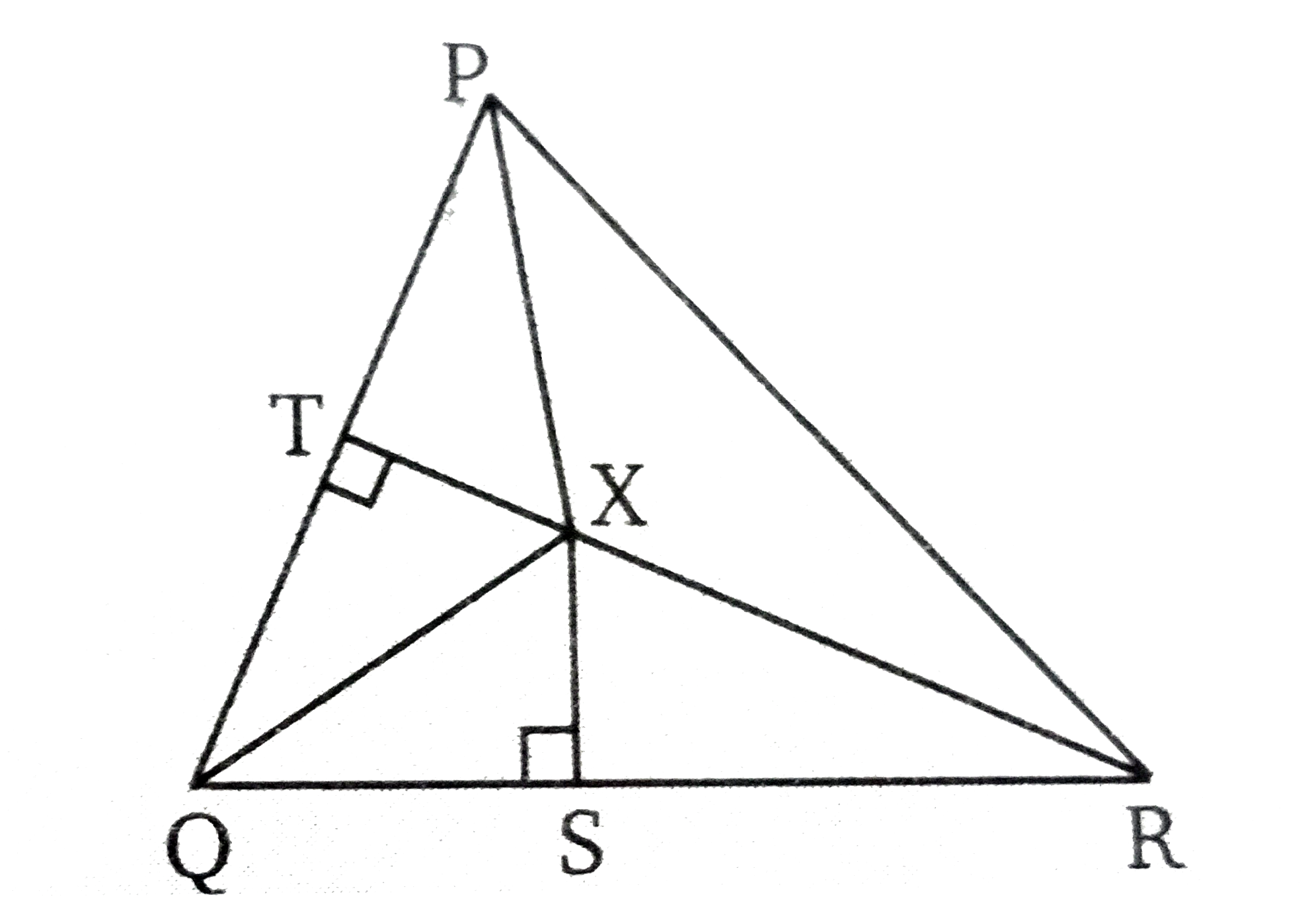
View Solutionदिये गये चित्र में ,QX तथा `RX, DeltaPQR` के क्रमश : `angleQ " तथा " angleR` के समद्विभाजक है यदि `XS bot QR" तथा " XT bot PQ` तो सिद्ध कीजिए -
(i) `DeltaXTQ = DeltaXSQ`
(ii) `PX , angleP` का समद्विभाजक है ।
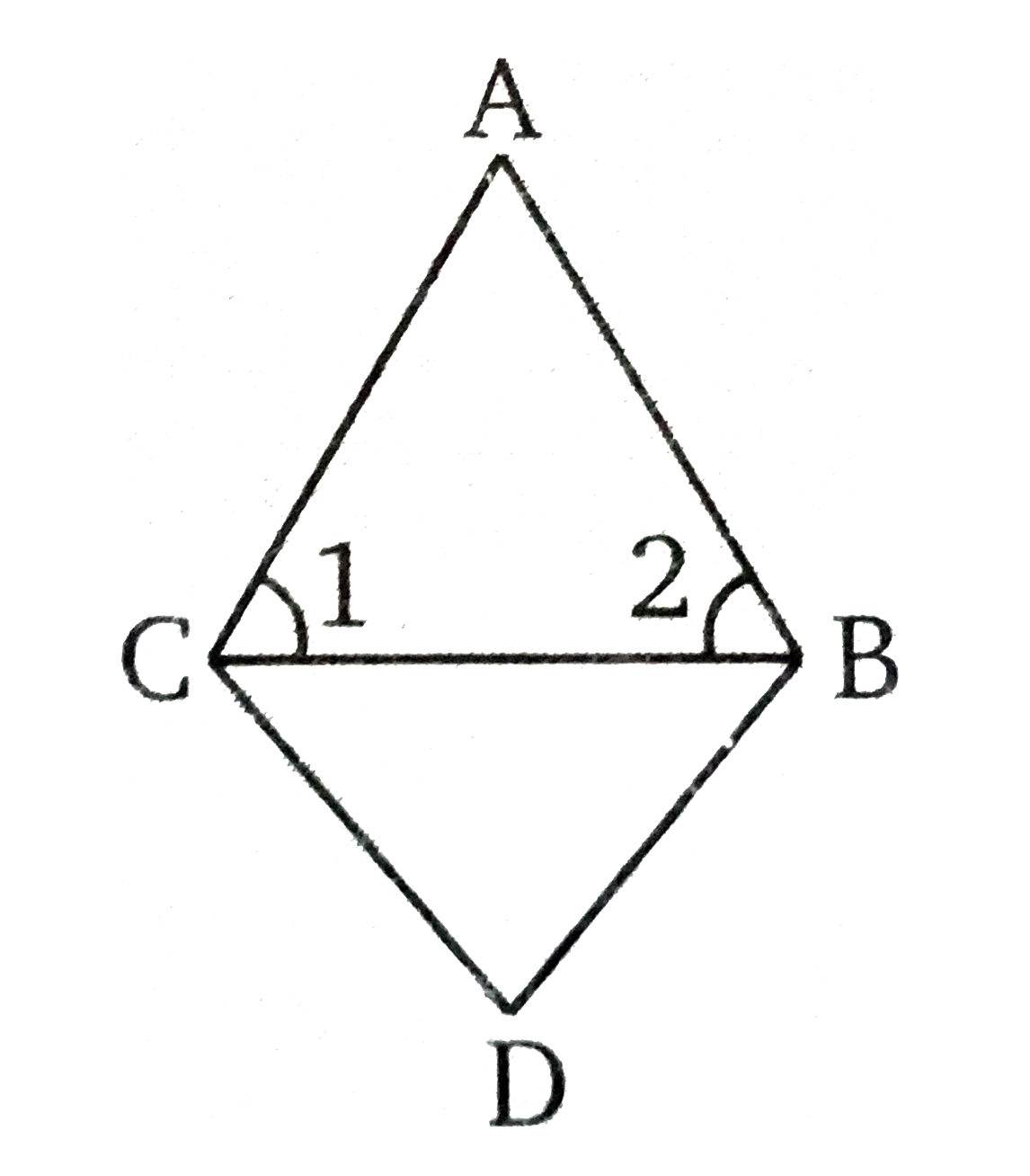
View Solutionचित्र में , `angle1 = angle2, AC bot CD" तथा " AB bot BD` तो सिद्ध कीजिए कि BD = CD
View Solutionदिये गये चित्र में , `AB = EF, BC = DE, AB bot BD" तथा" FE bot CE` तो सिद्ध कीजिए कि `DeltaABD cong Delta FEC`

View Solutionचित्र में ,`AB = AC` तथा `angleACD = 115^(@)," तब " angleBAC= ?`
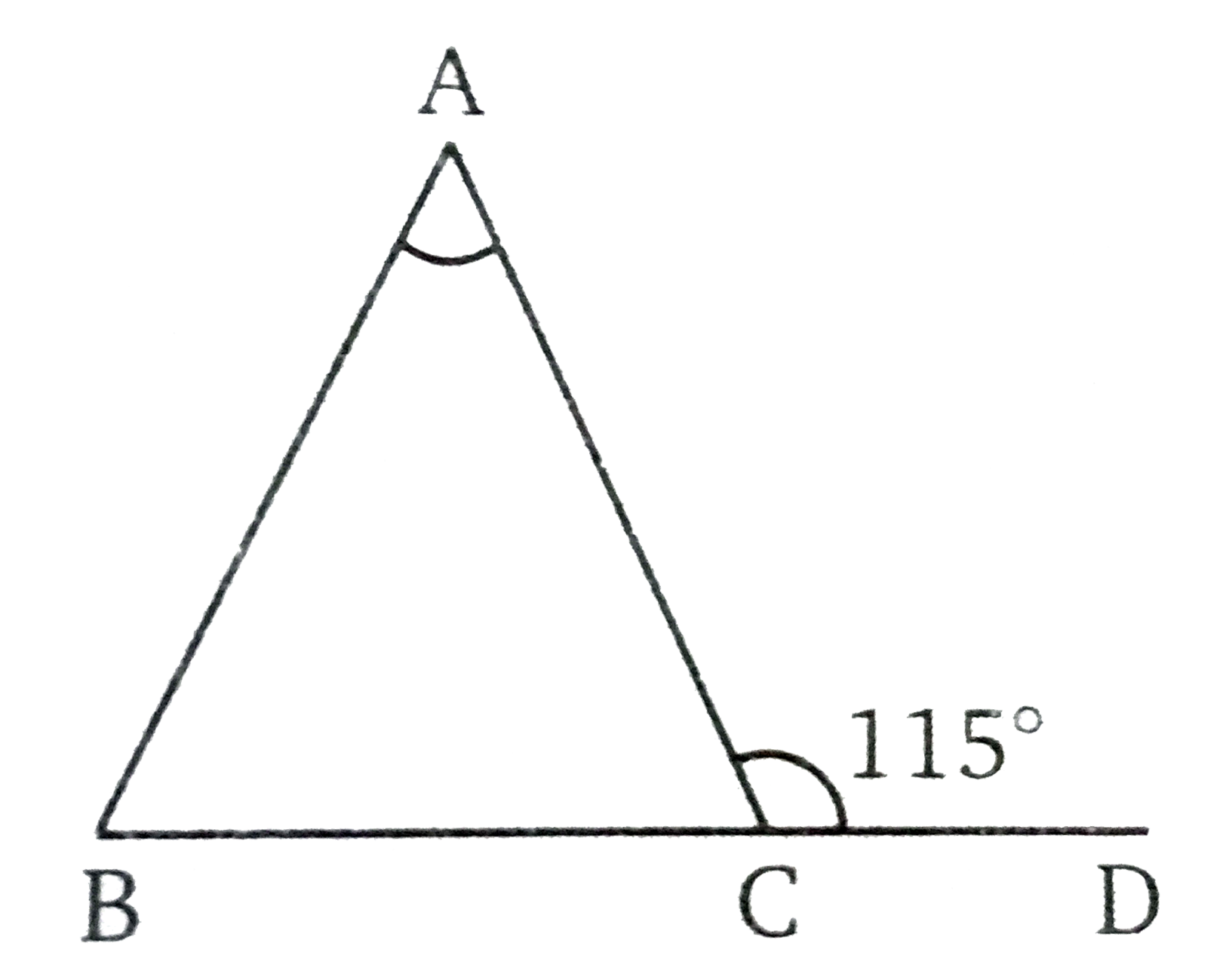
View Solution
अभ्यास प्रश्न 12.1 questions and complete solutions for chapter त्रिभुजों की सर्वांगसमता of SHREE BALAJI MATHS (HINDI) of Class 9