Complete Solutions to प्रश्नमाला 9C (बहुवैकल्पिक प्रश्न) of chapter त्रिभुजों की सर्वांगसमता एवं असमिकाएँ of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | त्रिभुजों की सर्वांगसमता एवं असमिकाएँ |
| BHARATI BHAWAN | प्रश्नमाला 9C (बहुवैकल्पिक प्रश्न) |
| Number Of Questions | 20 |
| Academic Year | 2023-24 |
निम्नांकित में से कौन-सा त्रिभुजों की सर्वांगसमता का नियम नहीं है?
View Solutionयदि एक त्रिभुज ABC में `angleA=50^(@)` तथा `angleB=60^(@)` है, तो सबसे बड़ी भुजा है
View Solutionयदि एक त्रिभुज की सबसे लंबी भुजा की लंबाई 12 cm हो, तो अन्य दो भुजाओं की लंबाइयाँ हो सकती हैं
View Solutionयदि `DeltaABC` में `angleA=100^(@),angleB=30^(@)` तथा `angleC=50^(@)` हो, तो
View Solutionयदि AB = QR, BC = RP तथा CA = PQ है, तो नीचे दिए गए कथनों में से कौन-सा सत्य है?
View Solutionयदि `DeltaPQR~=DeltaABC,PQ=5cm,angleQ=40^(@)` तथा `angleP=80^(@)` है, तो निम्नांकित में से कौन-सा कथन सत्य है?
View Solution`DeltaABC` में, `BC=AB` तथा `angleB=80^(@)` है। तब, `angleA=`?
View Solutionयदि `DeltaABC~=DeltaPQR` है, तो निम्नांकित में कौन सत्य नहीं है?
View Solution`DeltaABC` में,`angleC=angleA,BC=4`cm तथा `AC=5cm` है। तब, AB = ?
View Solution`DeltaABC` में, यदि `angleCgtangleB` हो, तो
View Solution`DeltaABC` तथा `DeltaDEF` में, `AB=FD,angleA=angleD` है। दोनों त्रिभुज SAS द्वारा सर्वांगसम होंगे यदि
View Solutionएक समकोण `DeltaDEF` में यदि `angleE=90^(@)` है, तो
View Solution`DeltaABC` में
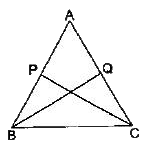
View Solutionआकृति में, AB = AC तथा AP = AQ है। सर्वांगसमता के किस प्रतिबंध के अधीन `DeltaPBC~=DeltaQCB` है?
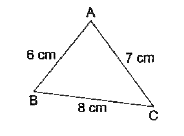
View Solution`DeltaABC` में `angleA=50^(@),angleB=60^(@)` है। निम्नांकित में से कौन-सा विकल्प त्रिभुज की भुजाओं की लंबाइयों को बढ़ते क्रम में दर्शाता है?
View Solutionएक त्रिभुज की दो भुजाओं की लंबाइयाँ क्रमशः 4 cm तथा 2 .5 cm है। निम्नांकित में से कौन-सी उसकी तीसरी भुजा की लंबाई नहीं हो सकती?
View Solution`DeltaABC` तथा `DeltaDEF` में, यदि AB = DE तथा BC = EF है, तो `DeltaABC~=DeltaDEF` होने के लिए आवश्यक है
View Solution`DeltaABC` तथा `DeltaDEF` में, यदि `angleB=angleE` तथा `angleC=angleF` है, तो `DeltaABC~=DeltaDEF` होने के लिए आवश्यक है
View Solution`DeltaABC` तथा `DeltaPQR` में यदि `AB=AC,angleC=angleP` तथा `angleB=angleQ` है, तो वे दोनों त्रिभुज
View Solutionयह संभव नहीं कि एक त्रिभुज बनाया जा सके जब भुजाएँ हों
View Solution
प्रश्नमाला 9C (बहुवैकल्पिक प्रश्न) questions and complete solutions for chapter त्रिभुजों की सर्वांगसमता एवं असमिकाएँ of BHARATI BHAWAN of Class 9