Complete Solutions to प्रश्नमाला 14 A of chapter हीरोन का सूत्र of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | हीरोन का सूत्र |
| BHARATI BHAWAN | प्रश्नमाला 14 A |
| Number Of Questions | 22 |
| Academic Year | 2023-24 |
एक त्रिभुज का क्षेत्रफल ज्ञात कीजिए जिसके आधार की लंबाई 24 cm है तथा संगत ऊँचाई 14.5 cm है।
View Solutionएक त्रिभुजाकार क्षेत्र के आधार की लंबाई उसकी ऊँचाई से तीन गुनी है। यदि Rs. 58 प्रति हेक्टेयर की दर से क्षेत्र की बुवाई की कुल लागत Rs. 783 है, तो क्षेत्र का आधार और ऊँचाई ज्ञात कीजिए।
View Solutionत्रिभुज का क्षेत्रफल ज्ञात कीजिए जबकि उसकी भुजाएँ 42 cm, 34 cm और 20 cm हैं। सबसे बड़ी भुजा के संगत त्रिभुज की ऊँचाई भी ज्ञात करें।
View Solutionएक त्रिभुज के तीनों भुजाओं की लंबाइयाँ क्मशः 10 cm, 24 cm तथा 26 cm हैं। 24 cm वाली भुजा के सम्मुख शीर्षबिंदु से इस भुजा पर डाले गए लंब की लंबाई ज्ञात कीजिए।
View Solutionयदि एक त्रिभुज की भुजाओं का अनुपात `5 : 12 : 13` और परिमाप 120 cm है, तो इसका क्षेत्रफल ज्ञात कीजिए। त्रिभुज के सबसे छोटे शीर्षलंब की लंबाई भी परिकलित कीजिए।
View Solutionएक समद्विबाहु त्रिभुज का क्षेत्रफल ज्ञात कीजिए जिसकी प्रत्येक समान भुजा 13 cm तथा आधार 20 cm है।
View Solutionएक समद्विबाहु त्रिभुज के आधार की लंबाई 80 cm है तथा उसका क्षेत्रफल `360 cm^(2)` है। त्रिभुज का परिमाप ज्ञात कीजिए।
View Solutionएक समद्विबाहु त्रिभुज का परिमाप 32 cm है। प्रत्येक समान भुजा की लंबाई का आधार से अनुपात `3 : 2` है। त्रिभुज का क्षेत्रफल ज्ञात कीजिए।
View Solutionएक त्रिभुज का परिमाप 50 cm है। त्रिभुज की एक भुजा उसकी सबसे छोटी भुजा से 4 cm लंबी है तथा तीसरी भुजा सबसे छोटी भुजा के दुगुने से 6 cm छोटी है। त्रिभुज का क्षेत्रफल ज्ञात कीजिए।
View Solutionएक पुल की त्रिभुजाकार दीवार की भुजाएँ 13 m, 14 m तथा 15 m है। इस दीवार पर इश्तहार लगाने का किराया Rs. 2000 प्रति `m^(2)` प्रतिवर्ष है। प्रचार के लिए उस दीवार का 6 माह तक उपयोग करने हेतु एक कंपनी की कुल लागत कितनी आएगी?
View Solutionएक समद्विबाहु त्रिभुज का परिमाप 42 cm है तथा उसके आधार की लंबाई, प्रत्येक समान भुजा की लंबाई की `1(1)/(2)` गुनी है (i) त्रिभुज की प्रत्येक भुजा की लंबाई, (ii) त्रिभुज का क्षेत्रफल तथा (iii) त्रिभुज की ऊँचाई ज्ञात कीजिए। `[sqrt7 = 2.64 "लीजिए।"]`
View Solutionयदि एक समबाहु त्रिभुज का क्षेत्रफल `36sqrt3 cm^(2)` है, तो उसका परिमाप ज्ञात कीजिए।
View Solutionयदि एक समबाहु त्रिभुज का क्षेत्रफल `81sqrt3 cm^(2)` है तो उसकी ऊँचाई ज्ञात कीजिए।
View Solutionएक समबाहु त्रिभुज की भुजा 8 cm है। उसका क्षेत्रफल हीरोन सूत्र द्वारा ज्ञात कीजिए। इसकी ऊँचाई भी ज्ञात कीजिए।
View Solutionएक समकोण त्रिभुज की सबसे लंबी भुजा 125 m है तथा शेष दो भुजाओं में से एक 100 m है। हीरोन के सूत्र का प्रयोग करते हुए, इसका क्षेत्रफल ज्ञात कीजिए।
View Solutionउस समकोण त्रिभुज का क्षेत्रफल और परिमाप ज्ञात कीजिए जिसकी कर्ण के अतिरिक्त भुजाएँ 18 cm और 80 cm है।
View Solutionएक समकोण त्रिभुज का परिमाप 24 cm है। यदि इसका कर्ण 10 cm है तो हीरोन सूत्र का प्रयोग कर त्रिभुज का क्षेत्रफल ज्ञात कीजिए।
View Solutionनीचे दी गई आकृति में छायांकित भाग का क्षेत्रफल ज्ञात कीजिए।
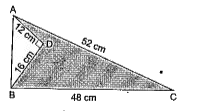
View Solution`Delta ABC` के अर्धपरिमाप तथा भुजाओं की लंबाइयों के अंतर क्रमशः 8cm,7 cm तथा 5cm हैं। त्रिभुज का क्षेत्रफल ज्ञात कीजिए।
View Solutionफर्श पर एक फूलों का डिजाइन 16 त्रिभुजाकार टाइलों से बनाया गया है, जिनमें से प्रत्येक की भुजाएँ 16cm, 12 cm तथा 20 cm हैं। इन टाइलों को Rs. 1 प्रति `cm^(2)` की दर से पॉलिश कराने का व्यय ज्ञात कीजिए।
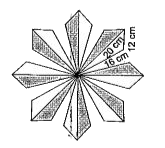
View Solutionकपड़े के 12 त्रिभुजाकार टुकड़ों को सीकर एक छाता बनाया गया है। प्रत्येक टुकड़े की माप `(50 cm xx 20 cm xx 50 cm)` है। छाते में कुल कितना कपड़ा लगा है?
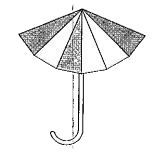
View Solutionयदि एक त्रिभुज की प्रत्येक भुजा को दुगुना कर दिया जाए तो उसके क्षेत्रफल में कितने प्रतिशत की वृद्धि हो जाएगी?
View Solution
प्रश्नमाला 14 A questions and complete solutions for chapter हीरोन का सूत्र of BHARATI BHAWAN of Class 9