Complete Solutions to EXAMPLES of chapter THEOREMS ON AREAS of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | THEOREMS ON AREAS |
| CALCUTTA BOOK HOUSE | EXAMPLES |
| Number Of Questions | 28 |
| Academic Year | 2023-24 |
D, E and F are the mid-points of the sides of BC, CA and AB of the `DeltaABC`. If `DeltaABC=16Sq.cm.,` then the area of the trapezium FBCE is-
View SolutionA, B, C, D are the mid-points of the sides PQ, QR, RS and SP respectively of the parallelogram PQRS. The area of PQRS = 36 Sq.cm. Then the area of the region ABCD is-
View SolutionO is any point inside the parallelogram ABCD. `DeltaAOB+DeltaCOD=16` sq.cm. Then the area of the parallelogram ABCD is-
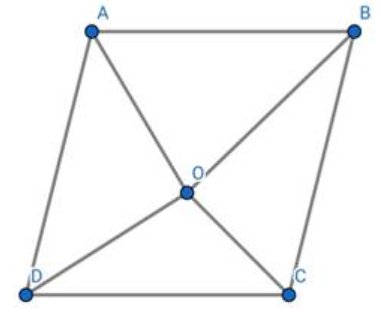
View SolutionD is the mid-point of BC of `DeltaABC`. E and O are the mid-points of BD and AE respectively. Then the area of the triangle BOE is-
View SolutionA parallelogram, a rectangle and a triangle are on the same base and between same parallels and their areas are P, R and T respectively, then
View SolutionPM is a median of the `DeltaPQR`. PM is extended to N such that PM = MN. If O be the mid-point of MN and if area of `DeltaPQR` be 40 sq.cm, then the area of the `DeltaQOM` is-
View SolutionDE is the perpendicular drawn from D of the parallelogram ABCD to its side AB and BF is the perpendicular drawn from B of ABCD to its side AD. If AB = 10cm, AD = 8 cm and DE = 6 cm, then find BF.
View SolutionThe area of the parallelogram ABCD is 100 sq. units. P is the mid-point of BC. Determine the area of the `DeltaABP`.
View SolutionAD is a medium of `DeltaABC` and P is a point on the side AC of `DeltaABC` such that area of `DeltaADP` : area of `DeltaABD` = 2 : 3, Determine the ratio (area of `DeltaPDC` : area of `DeltaABC`).
View SolutionABDE is a parallelogram. F is the mid-point of ED. If the area of the triangle ABD be 20 sq.cm, find the area of `DeltaAEF`.
View SolutionDetermine the length of the line joining between two points`(6,0) and (-2,0)`
View SolutionE is the mid-point of the medium AD of the `DeltaABC`. Prove that `DeltaBED=1/4DeltaABC`.
View SolutionDetermine the length of the line joining between two points`(4,3) and (2,1)`
View SolutionThe distance between the sides AB and DC of the rhombus ABCD is PQ and that between AD and BC is RS. Prove that PQ = RS.
View SolutionDetermine the length of the line joining between two points`(-2,-2) and (2,2)`
View SolutionDetermine the length of the line joining between two points`(0,-10) and (0,-3)`
View SolutionTwo triangles ABC and ABD of equal areas are on the opposite sides of AB. Prove that AB bisects CD equally.
View SolutionD is the mid-point of the side BC of the `DeltaABC`. The parallelogram CDEF lie between the same parallels CD and PQ, a parallel st. line of PQ through A. Prove that `DeltaABC` =parallelogram CDEF.
View SolutionP is any point on the diagonal BD of the parallelogram ABCD. Prove that `DeltaAPD=DeltaCPD`.
View SolutionAD and BE are the medians of the triangle ABC. Prove that `DeltaACD=DeltaBCE`.
View SolutionDetermine the length of the line joining between two points`(-7,0) and (-2,0)`
View SolutionIn `DeltaABC`, AB = AC. The perpendiculars drawn from B and C to AC and AB respectively, intersect the sides AC and AB at the points E and F respectively. Prove that FE||BC.
View SolutionIn triangle ABC, `angleABC=angleACB`. The bisectors of `angleABCandangleACB` intersect AC and AB at E and F respectively. Prove that FE||BC.
View SolutionDetermine the length of the line joining between two points`(0,15) and (0,4)`
View SolutionDetermine the length of the line joining between two points`(18,0) and (8,0)`
View SolutionFind that the point `(-5,0)` lie in which quadrant?
View SolutionFind the co ordinate on the Y axis cut by the straight line `2x-3y=12`
View SolutionFind the co ordinate on the X axis cut by the straight line `2x-3y=12`
View Solution
EXAMPLES questions and complete solutions for chapter THEOREMS ON AREAS of CALCUTTA BOOK HOUSE MATHS (BENGALI ENGLISH) of Class 9