Complete Solutions to Exercise 2.1 of chapter INTRODUCTION TO EUCLID'S GEOMETRY of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | INTRODUCTION TO EUCLID'S GEOMETRY |
| CPC CAMBRIDGE PUBLICATION | Exercise 2.1 |
| Number Of Questions | 7 |
| Academic Year | 2023-24 |
Which of the following statements are true and which are false? Give reasons for your answer.
(i) Only one line can pass through a single point.
(ii) There are infinite number of lines which pass through two distinct points.
(iii) A terminated line can be produced indefinitely on both the sides.
(iv) If two circles are equal, then their radii are equal.
(v) In given fig., `AB=PQ` and `PQ=XY`, then `AB=XY`.

View SolutionGive a definition for each of the following terms. Are there other terms that need to be defined first? What are they and how might you define them ?
(i) Parallel lines
(ii) Perpendicular lines
(iii) Line Segment
(iv) Radius of a circle
(v) Square
View SolutionConsider the two 'postulates' gives below:
(i) Given any two distinct points A and B, there exists a third point C, which is between A and B.
(ii) There exist at least three points that are not on the same line.
Do these postulates contain any undefined terms? Are these postulates consistent? Do they follow from Euclid's postulates? Explain.
View SolutionIf a point C lies between two points A and B, such that `AC=BC`, then prove that `AC=1/2 AB`. Explain by drawing the figure.

View SolutionIn question 4, point C is called a mid-point of line segment AB. Prove that every line segment has only one mid-point.
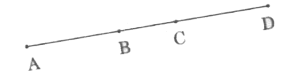
View SolutionIn the following figure, if `bar(AC)=bar(BD)`, then prove that `bar(AB)=bar(CD)`.
View SolutionWhy is axiom 5, in the list of Euclid's axiom considered on 'universal truth'? (Note that the question is not about the fifth postulate.)
View Solution
Exercise 2.1 questions and complete solutions for chapter INTRODUCTION TO EUCLID'S GEOMETRY of CAMBRIDGE MATHS (KANNADA ENGLISH) of Class 9