Complete Solutions to EXERCISE -7.1 of chapter QUADRILATERALS of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | QUADRILATERALS |
| CPC CAMBRIDGE PUBLICATION | EXERCISE -7.1 |
| Number Of Questions | 12 |
| Academic Year | 2023-24 |
The angles of quadrilateral are in the ratio `3:5:9:13`. Find all the angles of the quadrilateral.
View SolutionIf the diagonals of a parallelogram are equal, then show that it is rectangle .
View SolutionShow that if the diagonals of a quadrilateral bisect each other at right angles then it is a rhombus.
View SolutionShow that the diagonals of a square are equal and bisect each other at right angles.
View SolutionShow that if the diagonals of a quadrilateral are equal and bisect each other at right angles then it is a square.
View SolutionDiagonals AC of a parallelogram ABCD bisects `angleA`. Show that
it bisects `angleC` also
ABCD is a rhombus
View SolutionABCD is a rhombus Show that diagonal AC bisects `angleA` as well as `angleC` and diagonal BD bisects `angleB` as well as `angleD`.
View SolutionABCD is a rectangle in which diagonals AC bisects `angleA` as well as `angleC`, Show that
ABCD is a square
diagonal BD bisects `angleB` as well as `angleD`
View SolutionIn parallelogram ABCD two points P and Q are taken on diagonal BD such that DP=BQ show that
`DeltaAPD approx Delta CQB`
`DeltaAQB approx Delta CPD`
AQ=CP
APCQ is a parallelogram
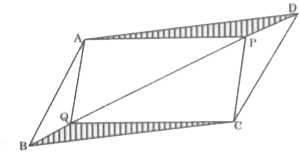
View SolutionABCD is a parallelogram and AP and CQ are perpendicular from vertices A and C on diagonal BD. Show that
`DeltaAPB approx DeltaCQD`
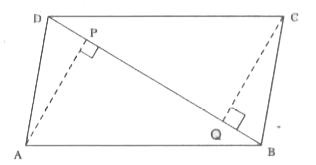
AP=CQ
View SolutionIn `DeltaABC and DeltaDEF, AB=DE,AB||DE, BC=EF and BC||EF` Vertices A,B and C are joined to vertices D , E and F respectively show that
quadrilateral ABED is a parallelogram
quadrilateral BEFC is a parallelogram
`AD||CF and AD=CF`
quadrilateral ACFD is a parallelogram
AC=DF
`DeltaABC approx DeltaDEF`.
View SolutionABCD is a trapezium in which `AB||CD and AD=BC` Show that
`angleA=angleB`
`angleC=angleD`
`DeltaABC approx DeltaBAD`
diagonal AC=diagonal BD
View Solution
EXERCISE -7.1 questions and complete solutions for chapter QUADRILATERALS of CAMBRIDGE MATHS (KANNADA ENGLISH) of Class 9