Complete Solutions to EXERCISE 12.6 of chapter CIRCLES of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | CIRCLES |
| CPC CAMBRIDGE PUBLICATION | EXERCISE 12.6 |
| Number Of Questions | 4 |
| Academic Year | 2023-24 |
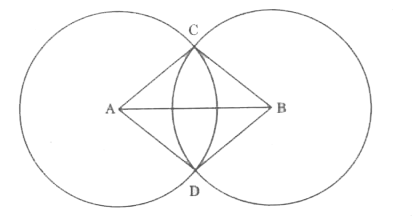
Prove that the line of centres of two intersecting circles subtends equal angles at the two point of intersection.
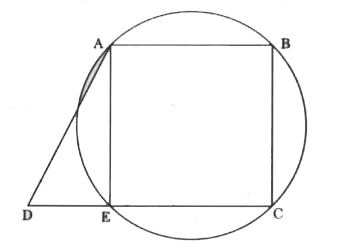
View SolutionABCD is a parallelogram. The circle through A, B and C intersect CD (produced if necessary) at E. Prove that AE = AD.
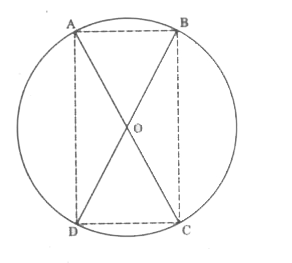
View SolutionAC and BD are chords of a circle which bisect each other. Prove that
(i) AC and BD are diameters,
(ii) ABCD is a rectangle.
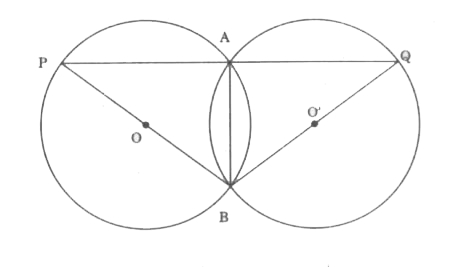
View SolutionTwo congruent circles intersect each other at points A and B. Through A any line segment PAQ is drawn so that P, Q lie on the two circles. Prove that BP = BQ.
View Solution
EXERCISE 12.6 questions and complete solutions for chapter CIRCLES of CAMBRIDGE MATHS (KANNADA ENGLISH) of Class 9