Complete Solutions to दीर्घ उत्तरीय प्रश्न of chapter चतुर्भुज (समांतर चतुर्भुज) of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | चतुर्भुज (समांतर चतुर्भुज) |
| DAS GUPTA | दीर्घ उत्तरीय प्रश्न |
| Number Of Questions | 12 |
| Academic Year | 2023-24 |
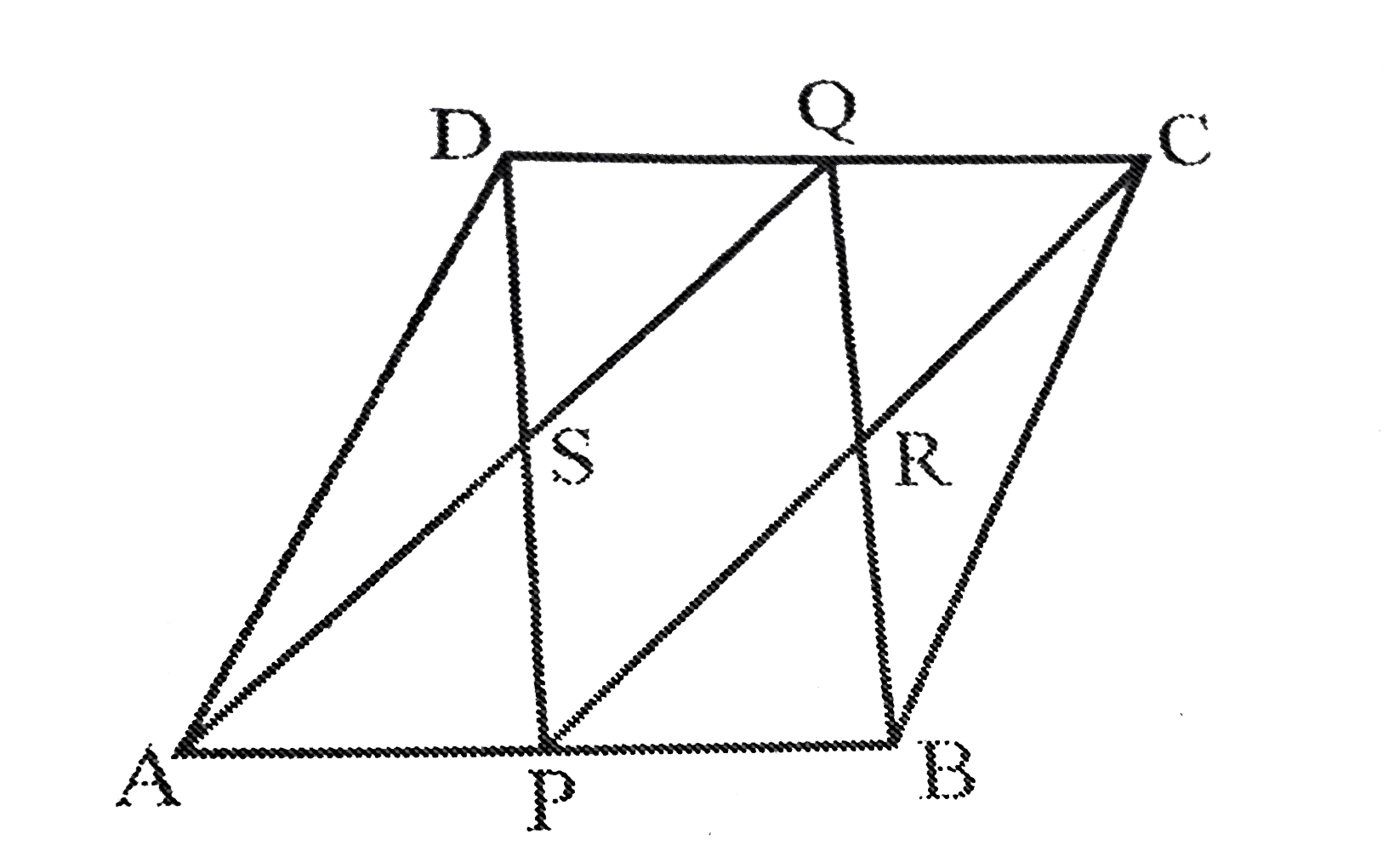
ABCD एक समांतर चतुर्भुज है । जिसमें P और Q क्रमश : सम्मुख भुजाओं AB और CD के मध्य - बिंदु है । ( देखिए आक्रति 8.18 ) | यदि AQ , DP को S पर प्रतिच्छेद करे और BQ ,CP को R पर प्रतिच्छेद करे , तो दर्शाइए कि :
(i) APCQ एक समांतर चतुर्भुज है ।
(ii) DPBQ एक समांतर चतुर्भुज है ।
(iii) PSQR एक समांतर चतुर्भुज है ।
View Solutionयदि एक तिर्यक रेखा दो समांतर रेखाओं को प्रतिच्छेद करती हो तो सिद्ध कीजिए कि अंतः कोणों के दो युग्मों के समद्विभाजकों से एक आयत बनता है।
View Solution`DeltaABC` और `DeltaDEF` में `AB||DE` और `BC||EF` और AB = DE ,BC = EF .
सिद्ध करें कि `AC=DF`
View Solutionसिद्ध करें कि समचतुर्भुज के विकर्ण एक-दूसरे के लंब समद्विभाजक हैं।
View Solutionसिद्ध करें कि किसी वर्ग की भुजाओं के मध्यबिंदुओं को क्रम से मिलानेवाली रेखाएं एक वर्ग बनाती हैं।
View Solutionसिद्ध करें कि किसी समचतुर्भुज के क्रमागत भुजाओं के युग्मों के मध्यबिंदुओं को मिलानेवाले रेखाखंडों से बना चतुर्भुज एक आयत होता है। अथवा चतुर्भुज ABCD एक समचतुर्भुज है और P,Q,R,S क्रमशः AB,BC,CD,DA के मध्यबिंदुएं हैं। सिद्ध कीजिए कि चतुर्भुज PQRS एक आयत है।
View Solutionएक चतुर्भुज ABCD के विकर्ण परस्पर लंब है। सिद्ध कीजिए कि इसकी भुजाओं के मध्यबिंदुों को मिलानेवाले रेखाखंडों से एक आयत बनता है।
View SolutionABCD एक समांतर चतुर्भुज है E और F उसकी सम्मुख भुजा AD और BC के मध्यबिंदु है। सिद्ध करें कि DEBF एक समांतर चतुर्भुज है एवं रेखाखंड BE और DF, विकर्ण AC को समत्रिभाजित करते है।
View Solutionत्रिभुज ABC में शीर्ष A से खींची गई रेखा AD माध्यिका है और E,AD का मध्यबिंदु है। BE को बढ़ाने पर यह AC से F पर मिलती है। सिद्ध कीजिए कि
`AF=1/3AC`.
View Solutionसिद्ध करें कि समलंब चतुर्भुज की असमांतर भुजाओं के मध्यबिंदुओं को मिलानेवाला रेखाखंड समांतर भुजाओं के समांतर और उनके योग का आधा होता है।
View SolutionABCD एक समलंब चतुर्भुज है जिसमें भुजा AB भुजा DC के समांतर है और E,AD का मध्यबिंदु है। यदि भुजा CB पर बिंदु G इस प्रकार हो कि रेखाखंड `EG||` भुजा DC तो सिद्ध करें कि `EG=1/2(AB+DC)`.
View Solutionसिद्ध करें कि वह सरल रेखा जो समलंब चतुर्भुज की एक असमांतर भुजा के मध्यबिंदु से उसकी समांतर भुजाओं के समांतर खींची गई है, दूसरी असमांतर भुजा को समद्विभाजित करती है।
View Solution
दीर्घ उत्तरीय प्रश्न questions and complete solutions for chapter चतुर्भुज (समांतर चतुर्भुज) of BHARATI BHAWAN MATHS (HINDI) of Class 9