Complete Solutions to अभ्यास के लिए of chapter त्रिभुज of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | त्रिभुज |
| DEEPAK PUBLICATION | अभ्यास के लिए |
| Number Of Questions | 11 |
| Academic Year | 2023-24 |
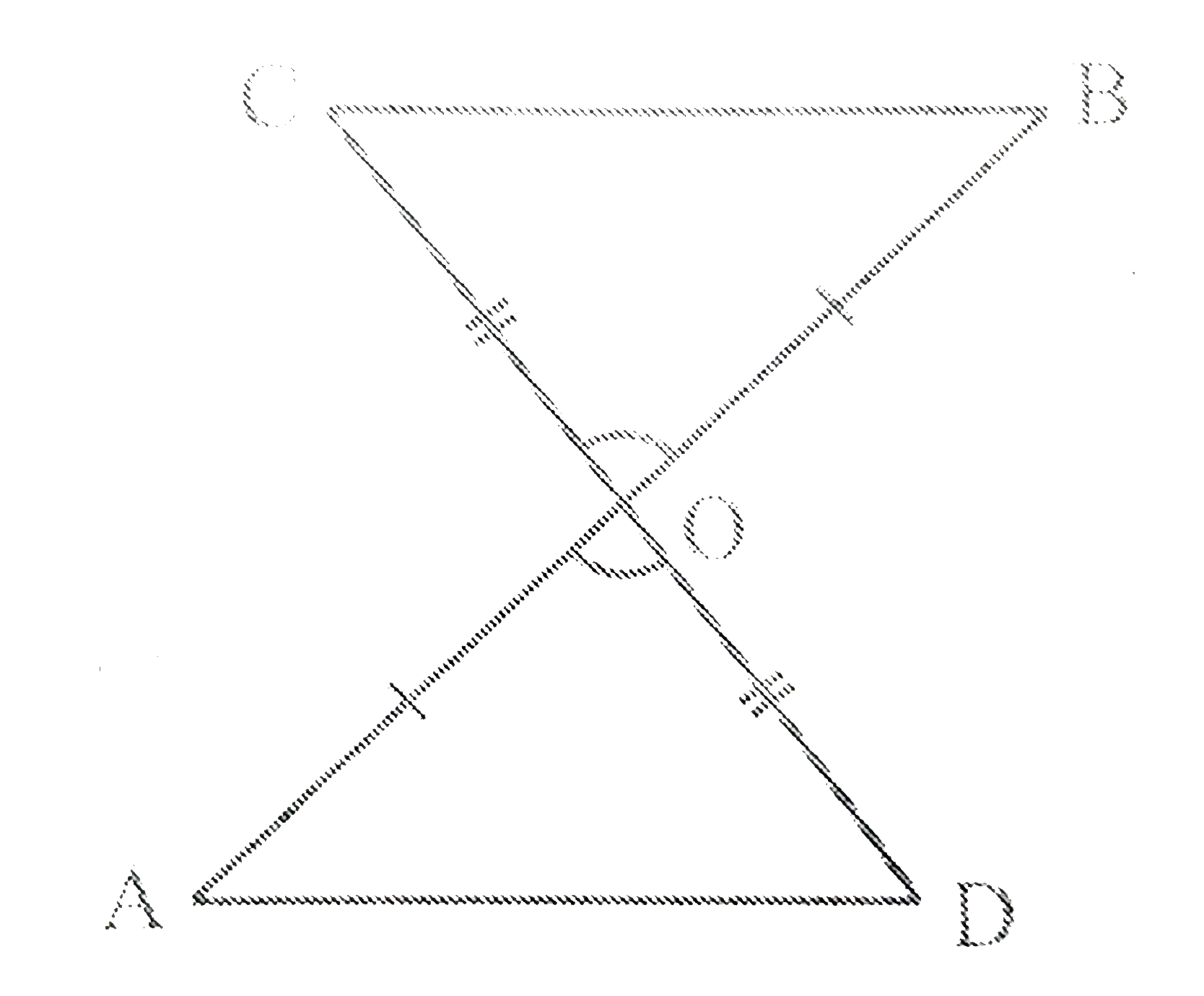
आकृति में OA = OB और OD = OC है। दर्शाइए कि
(i) `Delta AOD ~= Delta BOC ` और (ii) AD || BC है।
View SolutionAB एक रेखाखंड है और रेखा `l` इसका लम्ब समद्विभाजक है। यदि `l` पर स्थित P कोई बिंदु है, तो दर्शाइए कि P बिंदुओं A और B से समदूरस्थ (equidistant) है।
View Solutionरेखाखंड AB एक अन्य रेखाखंड CD के समांतर है और O रेखाखंड AD का मध्य बिंदु है (देखिए चित्र) | दर्शाइए कि (i) `DeltaAOB~=DeltaDOC` (ii) O रेखाखंड BC का भी मध्य बिंदु है |
View Solutionसिद्ध कीजिए कि किसी समद्विबाहु त्रिभुज में बराबर भुजाओं के सम्मुख कोण बराबर होते है।
View Solutionयदि किसी त्रिभुज के दो कोण समान हों तो उनकी सम्मुख भुजाएँ समान होती हैं।
View SolutionE और F क्रमश: त्रिभुज ABC की बराबर भुजाओ AB और AC के मध्यें-बिंदु है दर्शाइए की BF=CE है
View Solutionयदि किसी त्रिभुज के एक कोण का समद्विभाजक सम्मुख भुजा को समद्विभाजित करता हो , तो सिद्ध कीजिए कि त्रिभुज समद्विबाहु त्रिभुज है ।
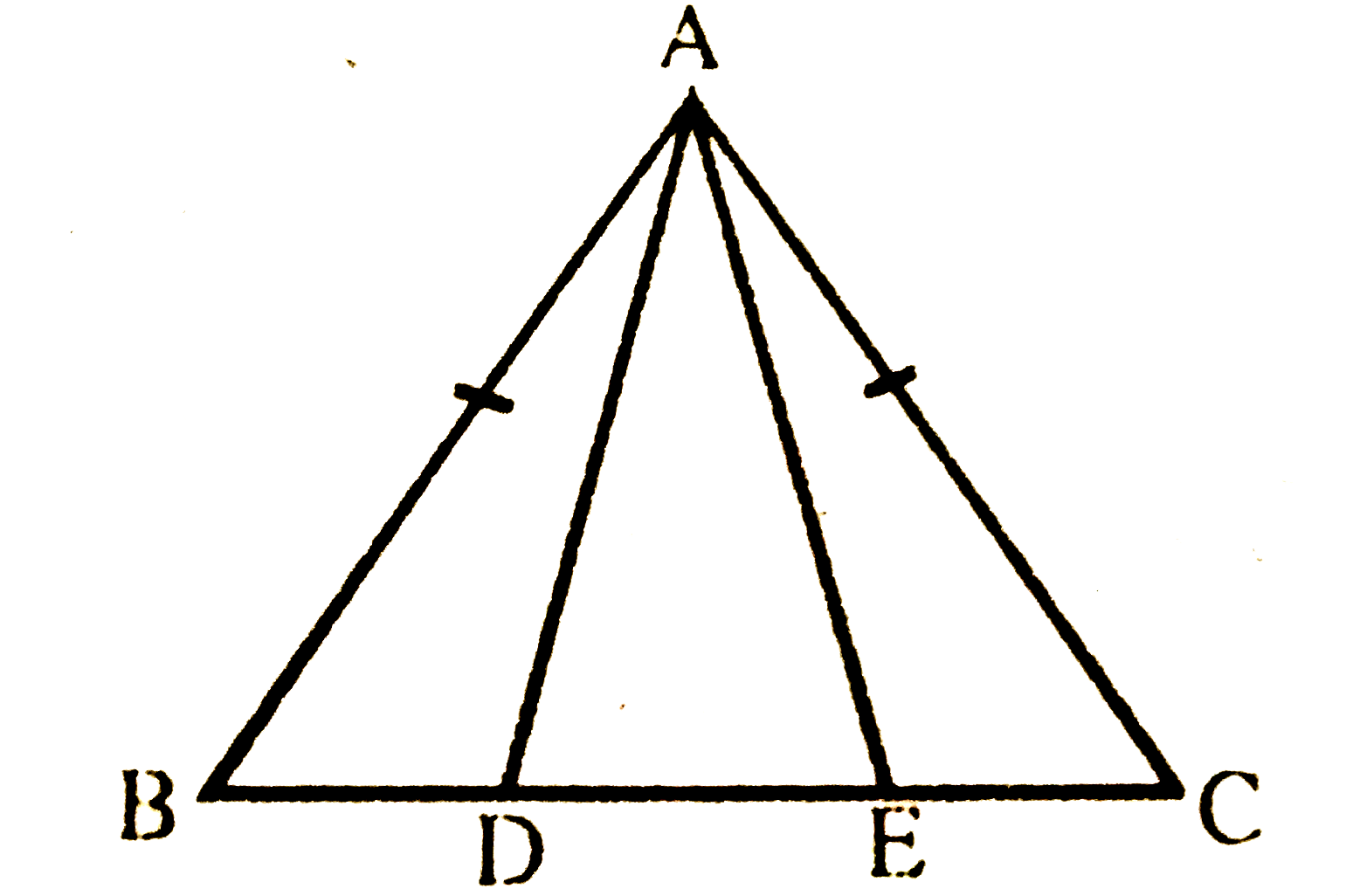
View Solutionएक समद्विबाहु त्रिभुज ABC जिसमें AB = AC है, की भुजा BC पर दो बिंदु D और E इस प्रकार हैं कि BE = CD है (देखिए चित्र) | दर्शाइए कि AD = AE है |
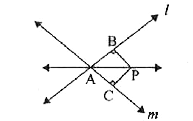
View Solutionबिंदु A पर प्रतिच्छेद करने वाली दो रेखाओं l और m से समदूरस्थ एक बिंदु P है (देखिए आकृति)। दर्शाइए कि रेखा AP दोनों रेखाओं के बीच के कोण को समद्विभाजित करती है।
View Solutionत्रिभुज PQR में कोण P, Q तथा R के माप आपस में समान हैं। सिद्ध करें कि `DeltaPQR` समबाहु त्रिभुज है।
View Solutionसमद्विबाहु त्रिभुज का प्रत्येक कोण को डिग्री में लिखें यदि
`DeltaABC` में यदि `angleA=100^(@)` और AB = AC हो, तो `angleB` तथा `angleC` ज्ञात करें |
View Solution
अभ्यास के लिए questions and complete solutions for chapter त्रिभुज of DEEPAK PUBLICATION of Class 9