Complete Solutions to अभ्यास के लिए प्रश्न of chapter समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल |
| DEEPAK PUBLICATION | अभ्यास के लिए प्रश्न |
| Number Of Questions | 6 |
| Academic Year | 2023-24 |
चित्र में , ABCD एक समान्तर चतुर्भुज है तथा EFCD एक आयत है। साथ ही `AL bot DC `, तो सिद्ध कीजिए कि
`(i) ar(ABCD) =ar(EFCD) " "(ii) ar(ABCD)=DCxxAL`
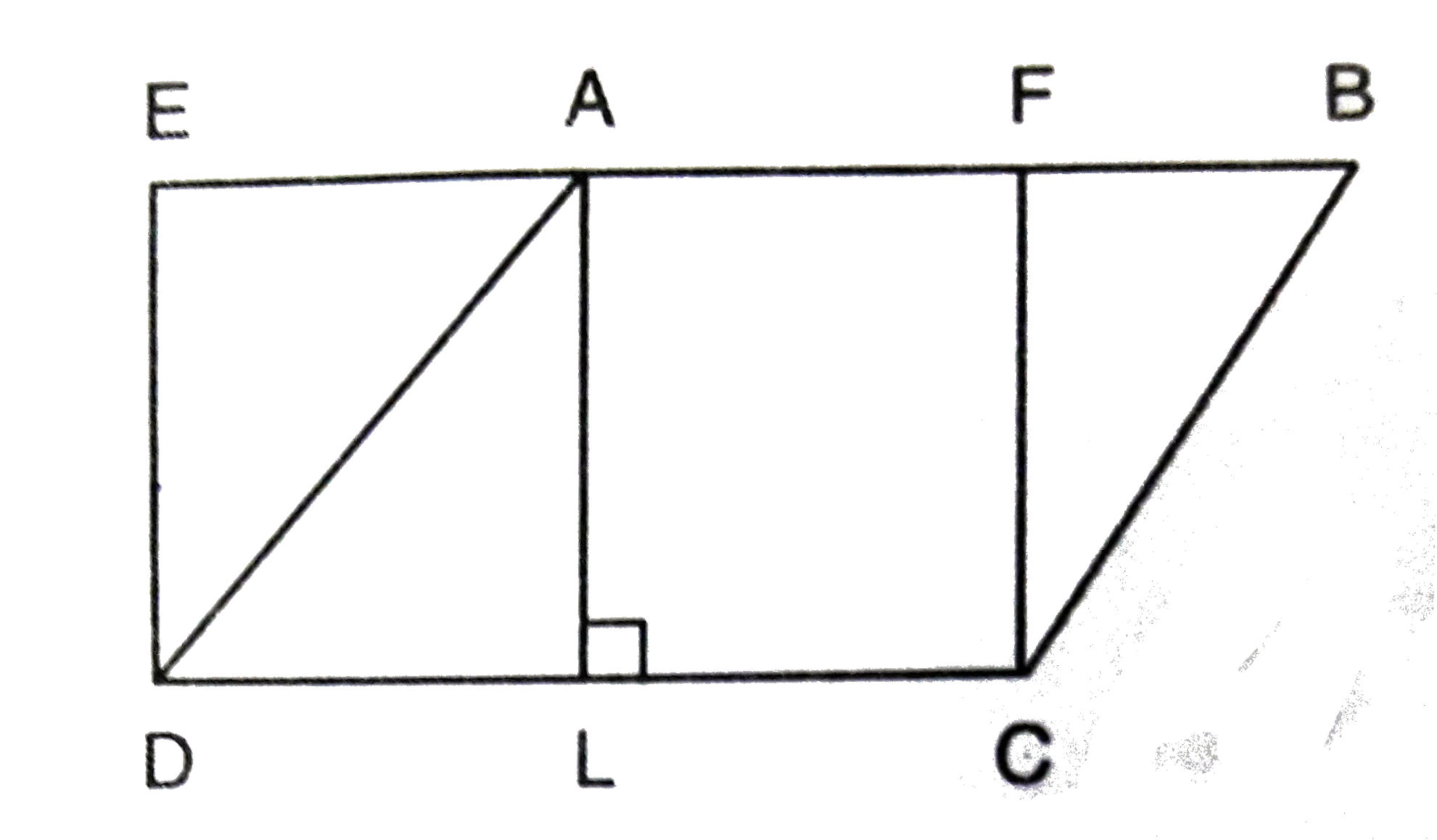
View Solutionचित्र में , ABCD एक समान्तर चतुर्भुज है तथा EFCD एक आयत है। साथ ही `AL bot DC `, तो सिद्ध कीजिए कि
`(i) ar(ABCD) =ar(EFCD) " "(ii) ar(ABCD)=DCxxAL`

View Solutionयदि एक त्रिभुज और एक समान्तर चतुर्भुज एक ही आधार और एक ही समान्तर रेखाओं के बीच स्थित हों, तो सिद्ध कीजिए कि त्रिभुज का क्षेत्रफल समान्तर चतुर्भुज का क्षेत्रफल का आधा होता है।
View Solutionआक्रति 9.22 में ,ABCD एक चतुर्भुज है और BE ।। AC इस प्रकार है कि BE बढ़ाई गई DC को E पर मिलती है । दर्शाइए कि त्रिभुज ADE का क्षेत्रफल चतुर्भुज ABCD के क्षेत्रफल के बराबर है ।

View Solutionचित्र में ABCD एक चतुर्भुज है तथा BD इसका एक विकर्ण है । सिद्ध कीजिए कि ABCD एक समांतर चतुर्भुज है तथा इसका क्षेत्रफल ज्ञात कीजिए।
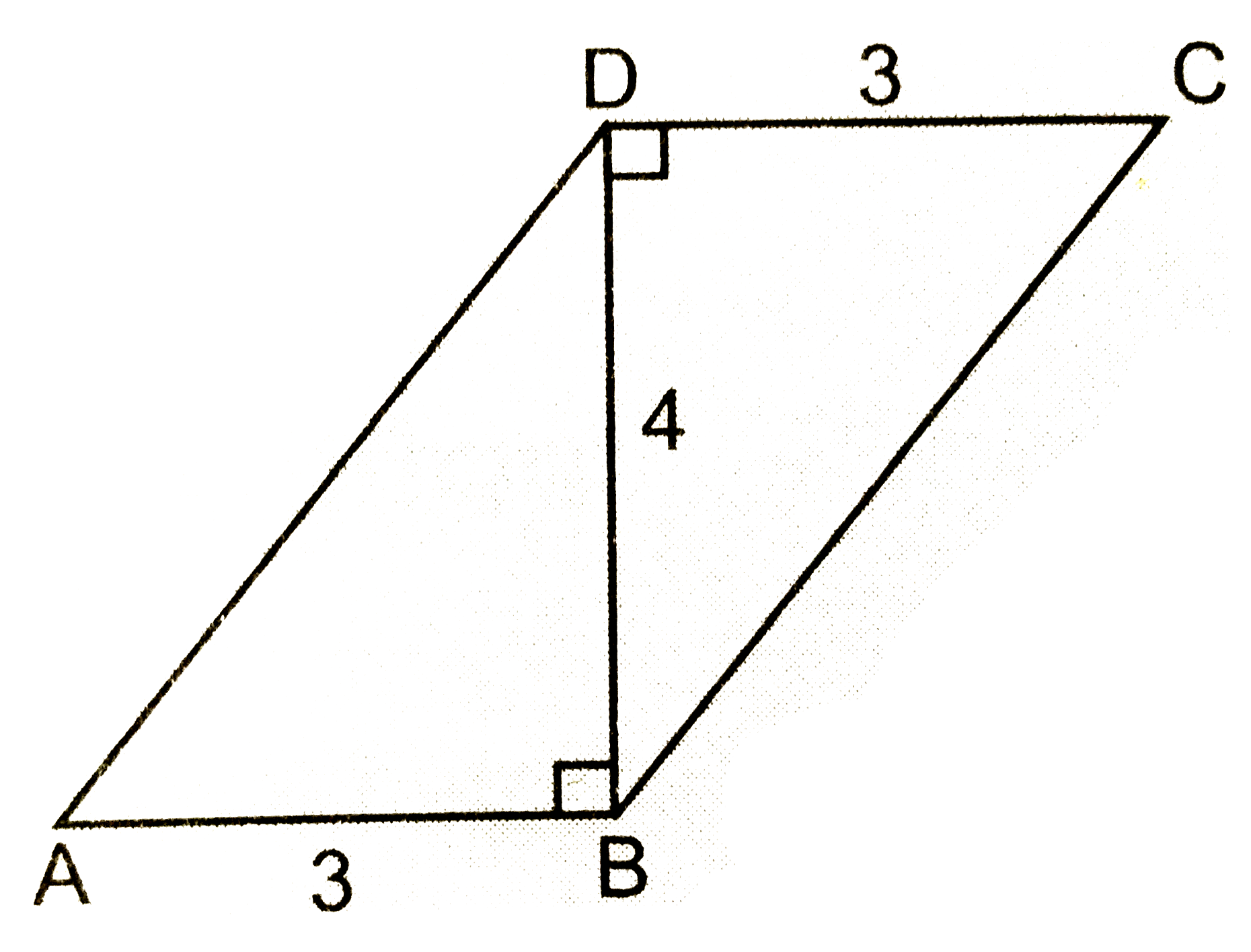
View Solutionसमांतर चतुर्भुज ABCD में, AB = 12 सें०मी० हैं। भुजाओं AB तथा AD के संगत शीर्षलंब क्रमशः 6 सें०मी० तथा 8 सें०मी० हैं जैसे कि आकृति में दिखाया गया है। AD ज्ञात करें।

View Solution
अभ्यास के लिए प्रश्न questions and complete solutions for chapter समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल of DEEPAK PUBLICATION of Class 9