Complete Solutions to प्रश्नावली 10.5 of chapter वृत्त of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | वृत्त |
| DEEPAK PUBLICATION | प्रश्नावली 10.5 |
| Number Of Questions | 12 |
| Academic Year | 2023-24 |
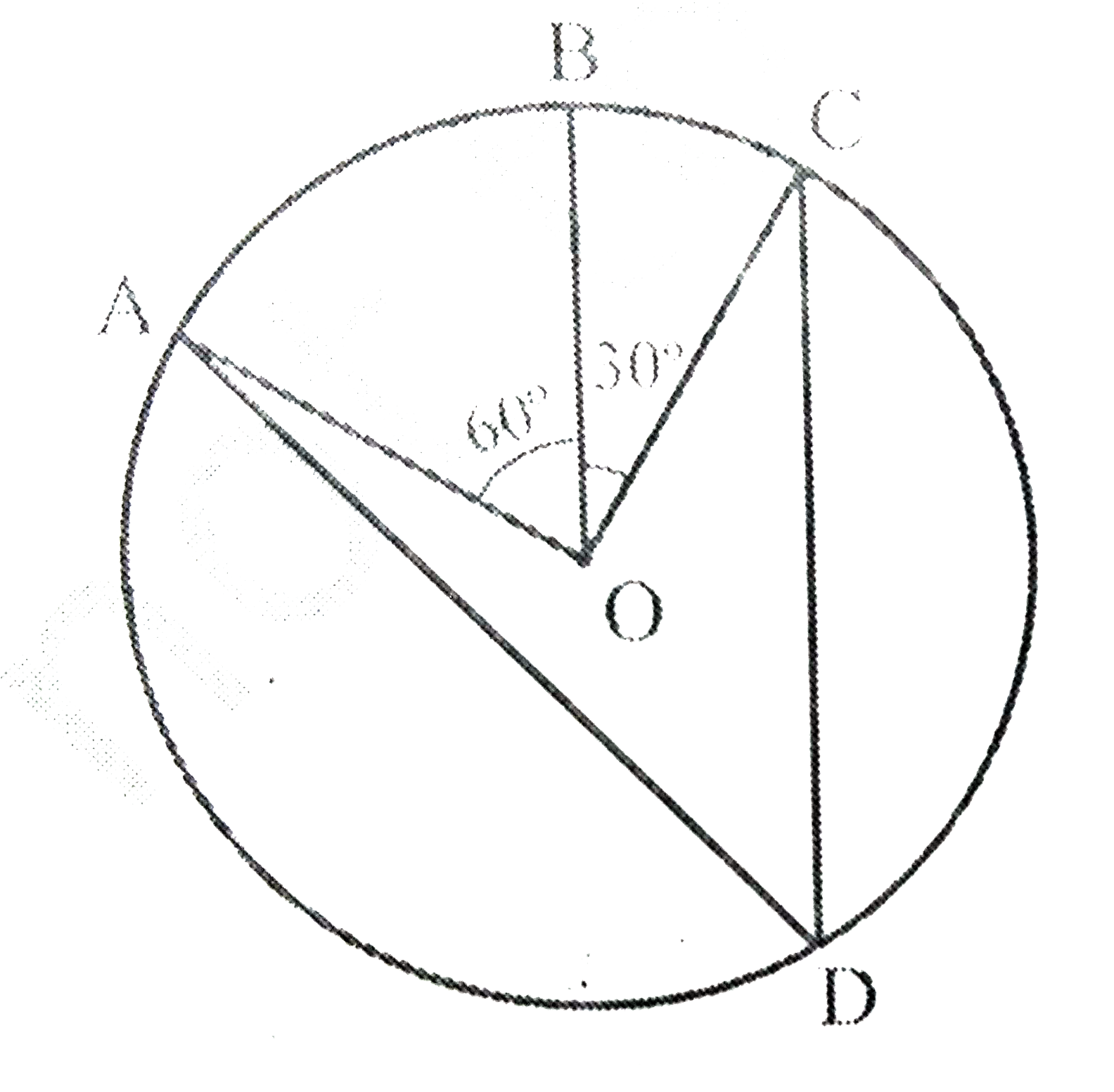
आकृति 10.36 में, केंद्र O वाले एक वृत्त पर तीन बिंदु A , B और C इस प्रकार है कि `angle BOC=30^(@)` तथा `angleAOB=60^(@)` है यदि चाप ABC के अतिरिक्त वृत्त पर D एक बिंदु है तो `angleADC` ज्ञात कीजिए ।
View Solutionकिसी वृत्त की एक जीवा वृत्त की त्रिज्या के बराबर है। जीवा द्वारा लघु चाप के किसी बिंदु पर अंतरित कोण ज्ञात कीजिए तथा दीर्घ चाप के किसी बिंदु पर भी अंतरित कोण ज्ञात कीजिए
View Solutionआकृति 10 .37 में, `angle PQR=100^(@)` है जहाँ P , Q तथा R केंद्र O वाले एक वृत्त पर स्थित बिंदु है `angle OPR` ज्ञात कीजिए

View Solutionआकृति में, `/_ABC= 69^(@)` और `/_ACB= 31^(@)` हो, तो `/_BDC` ज्ञात कीजिए।

View Solutionएक वृत्त पर A , B , C और D चार बिंदु है । AC और BD एक बिंदु E पर इस प्रकार प्रतिच्छेद करते है कि `angle BEC=130^(@)` तथा `angle ECD=20^(@)` है `angle BAC` ज्ञात कीजिए

View SolutionABCD एक चक्रीय चतुर्भुज है जिसके विकर्ण एक बिंदु E पर प्रतिच्छेद करते है । यदि `angleDBC=70^(@)` और `angleBAC=30^(@)` हो , तो `angle BCD` ज्ञात कीजिए । पुन: यदि AB = BC हो, तो `angle ECD` ज्ञात कीजिए
View Solutionयदि एक चक्रीय चतुर्भुज के विकर्ण उसके शीर्षो से जाने वाले वृत्त के व्यास हो, तो सिद्ध कीजिए कि वह एक आयत है ।
View Solutionयदि एक समलंब की असमान्तर भुजाएँ बराबर हो, तो सिद्ध कीजिए कि वह चक्रीय है ।
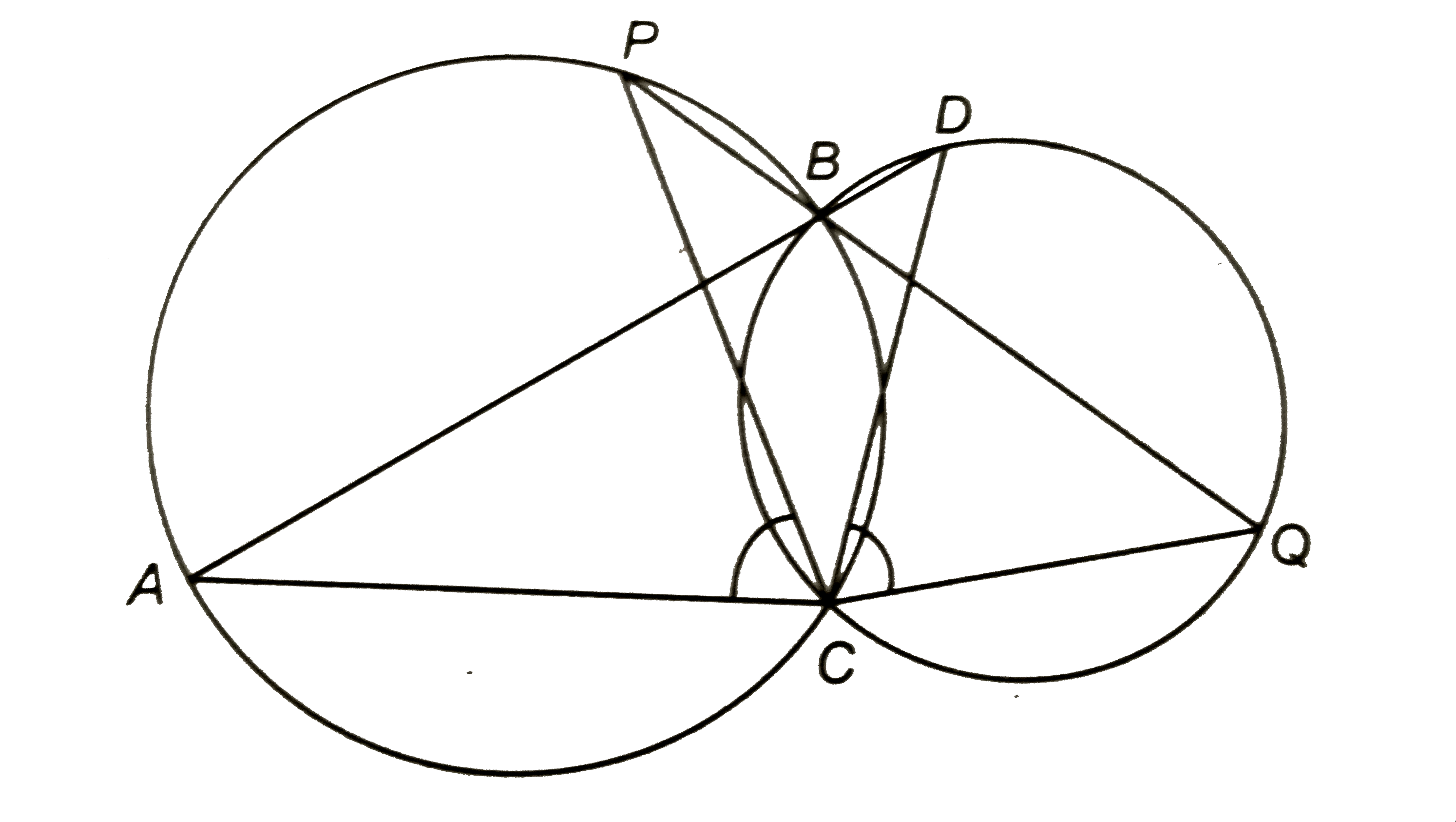
View Solutionदो वृत्त दो बिन्दुओं B और C पर प्रतिच्छेद करते हैं | B से होने वाले दो रेखाखण्ड ABD और PBQ वृत्तों को A, D और P, Q पर क्रमश: प्रतिच्छेद करते हुए खींचे गए हैं (आकृति देखिए) | सिद्ध कीजिए कि `angleACP=angleQCD` है |
View Solutionयदि किसी त्रिभुज की दो भुजाओ को व्यास मानकर वृत्त खींचे जाएं , तो सिद्ध कीजिए कि इन वृत्तों का प्रतिच्छेद बिंदु तीसरी भुजा पर स्थित है ।
View Solutionउभयनिष्ट कर्ण AC वाले दो समकोण त्रिभुज ABC और ADC है । सिद्ध कीजिए कि `angleCAD=angle CBD` है
View Solutionसिध्द कीजिए कि चक्रीय कि चक्रीय समांतर चतुर्भुज आयत होता है।
View Solution
प्रश्नावली 10.5 questions and complete solutions for chapter वृत्त of DEEPAK PUBLICATION of Class 9