Complete Solutions to Exercise 1.5 of chapter SET LANGUAGE of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | SET LANGUAGE |
| FULL MARKS | Exercise 1.5 |
| Number Of Questions | 11 |
| Academic Year | 2023-24 |
Using the adjacent venn diagram, find the following sets :
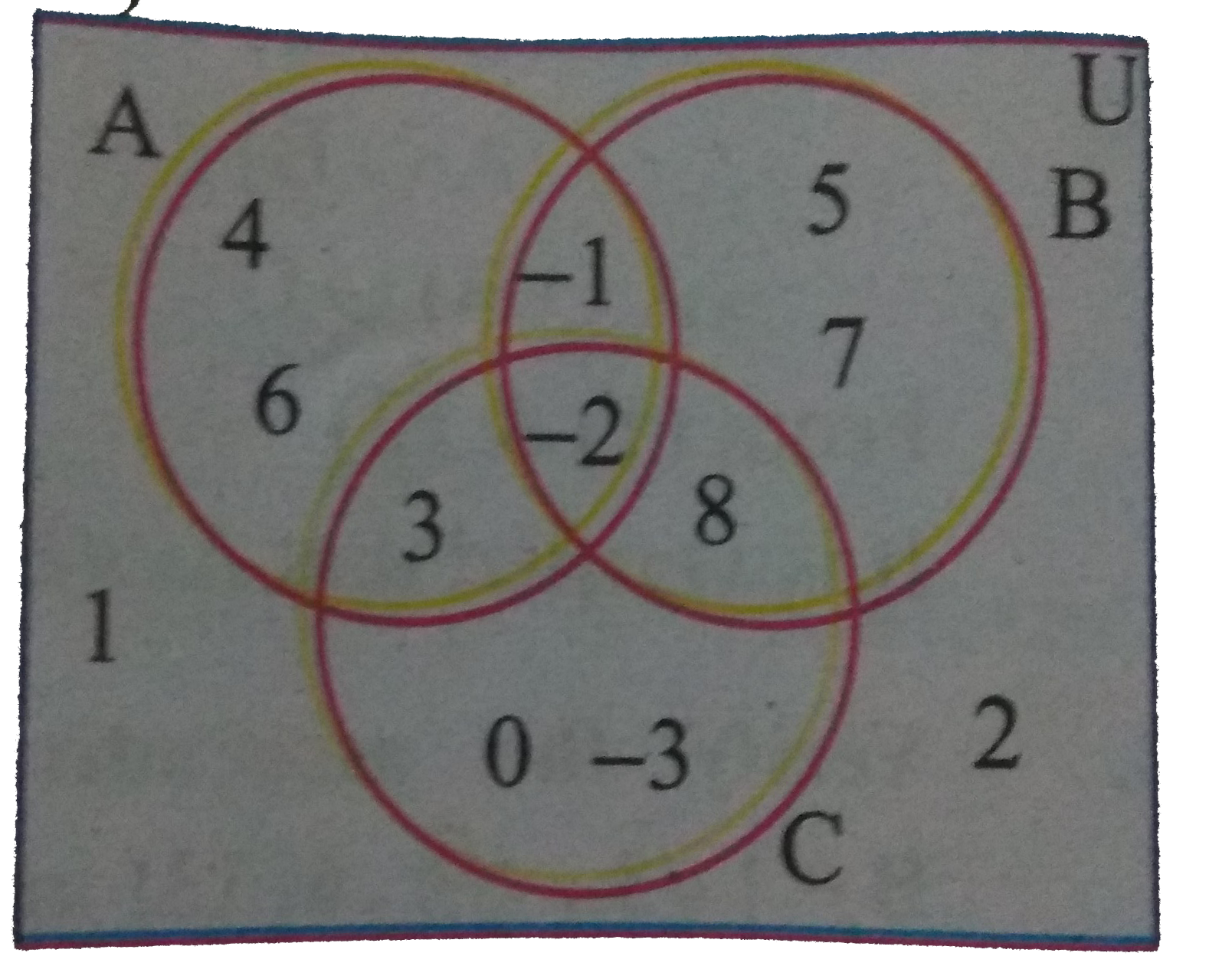
(i) A - B
(ii) B - C
(iii) `A'cupB'`
(iv) `A'capB'`
(v) `(BcupC)'`
(vi) `A-(BcupC)`
(vii) `A-(BcapC)`
View SolutionIf K = {a, b, d, e, f}, L = {b, c, d, g} and M = (a, b, c, d, h} then find the following:
`Kcup(LcapM)` and verify distributive laws.
View SolutionFor `A={x : x in Z, -2 lt x le 4}. B={x : x in W, x le 5}, C={-4,-1,0,2,3,4} " verify "A cup (B nn C) =(A cup B) nn (A cup C)`.
View SolutionVerify `Acup(BcapC)=(AcupB)cap(AcupC)` using Venn diagrams.
View SolutionIf A = {b, c, e, g, h}, B = {a, c, d, g, i} and C = {a, d, e, g, h}, then show that `A-(BcapC)=(A-B)cup(A-C)`.
View SolutionIf `A={x:x=6n,ninWandnlt6},B={x:x=2n,ninNNand2ltnle9}andC={x:x=3n,ninNNand4lenlt10}`, then show that `A-(BcapC)=(A-B)cup(A-C)`
View SolutionIf A = {-2, 0, 1, 3, 5}, B = {-1, 0, 2, 5, 6} and C = {-1, 2, 5, 6, 7}, then show that `A-(BcupC)=(A-B)cap(A-C)`.
View SolutionIf `A={y:y=(a+1)/2,ainWandale5},B={y:y=(2n-1)/2,ninWandnlt5}andC={-1,-1/2,1(3)/(2),2}`, then show that `A-(BcupC)=(A-B)cap(A-C)`.
View SolutionVerify `A-(BcapC)=(A-B)cup(A-C)` using Venn diagrams.
View SolutionIf U = {4, 7, 8, 10, 11, 12, 15, 16}, A = {7, 8, 11, 12} and B = {4, 8, 12, 15}, then verify De Morgan's Laws for complementation.
View SolutionVerify `(AcapB)'=A'cupB'` using Venn diagrams.
View Solution
Exercise 1.5 questions and complete solutions for chapter SET LANGUAGE of FULL MARKS MATHS (TAMIL ENGLISH) of Class 9
All Exercises from FULL MARKS Class 9 MATHS SET LANGUAGE
- Additional Questions II. Answer the following questions.
- Additional Questions (I. Choose The Correct Option)
- Assignment (I. Fill in the blanks)
- Assignment (II. Choose the correct answer)
- Assignment (III. Answer the following questions.)
- Exercise 1.1
- Exercise 1.2
- Exercise 1.3
- Exercise 1.4
- Exercise 1.5
- Exercise 1.6
- Exercise 1.7 (MCQ)
- Text Book Activities
- Thinking Corner