Complete Solutions to 4 MARKS QUESTIONS of chapter PYTHAGORAS THEOREM of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | PYTHAGORAS THEOREM |
| OSWAL | 4 MARKS QUESTIONS |
| Number Of Questions | 9 |
| Academic Year | 2023-24 |
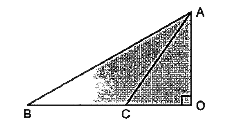
In triangle ABC, given below, AB = 8 cm, BC = 6 cm and AC = 3 cm. Calculate the length of OC
View SolutionIn the given figure, `AB||CD, AB=7cm, BD=25 cm and CD=17cm`, find the length of side BC.

View SolutionIn `DeltaABC, angleB=90^(@)`, find the sides of the triangle, if :
(i) `AB=(x-3)cm, BC=(x+4)cm and AC=(x+6)cm`
(ii) `AB=xcm, BC=(4x+4)cm and AC=(4x+5)cm`
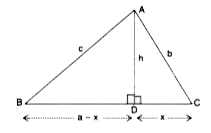
View SolutionIn the figure, given below, AD `_|_` BC.
Prove that : `c^(2)=a^(2)+b^(2)-2ax`.
View SolutionM and N are the mid-points of the sides QR and PQ respectively of a `DeltaPQR`, right-angled at Q. Prove that :
(i) `PM^(2)+RN^(2)=5MN^(2)`
(ii) `4PM^(2)=4PQ^(2)+QR^(2)`
(iii) `4RN^(2)=PQ^(2)+4QR^(2)`
(iv) `4(PM^(2)+RN^(2))=5PR^(2)`
View SolutionO is any point inside a rectangle ABCD. Prove that `O B^2+O D^2=O A^2+O C^2`.
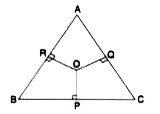
View SolutionIn the following figure, OP, OQ and OR are drawn perpendiculars to the sides BC, CA and AB repectively of triangle ABC. Prove that :
`AR^(2)+BP^(2)+CQ^(2)=AQ^(2)+CP^(2)+BR^(2)`
View SolutionIn the following figure, AD is perpendicular to BC and D divides BC in the ration 1 : 3.
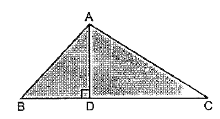
Prove that : `2AC^(2)=2AB^(2)+BC^(2)`
View SolutionIn the given figure, triangle ABC is a right triangle with `angleB=90^(@) and D` is mid-point of side BC. Prove that :
`AC^(2)=AD^(2)+3CD^(2)`

View Solution
4 MARKS QUESTIONS questions and complete solutions for chapter PYTHAGORAS THEOREM of ICSE of Class 9