Complete Solutions to Questions of chapter RECTILINEAR FIGURES of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | RECTILINEAR FIGURES |
| SELINA PUBLICATION | Questions |
| Number Of Questions | 23 |
| Academic Year | 2023-24 |
The sum of the interior angles of a polygon is five times the sum of its exterior angles. Find the number of sides in the polygon.
View SolutionOne angle of an eight-sided polygon is `100^(@)` and the other angles are equal. Find the measure of each equal angle.
View SolutionIn a pentagon ABCDE, AB is parallel to ED and angle `B= 140^(@)`. Find the angles C and D, if `angleC: angleD= 5: 6`
View SolutionIn the pentagon ABCDE, angle `A= 110^(@)`, angle B= `140^(@)` and angle D= angle E. The sides AB and DC, when produced, meet at right angle. Calculate angles BCD and E.
View SolutionBy dividing into triangles, find the sum of the angles of the doubly re-entrant heptagon ABCDEFG as shown alongside. Does the general value of `(2n-4)` right-angles hold for re-entrant polygon?

View SolutionEach interior angle of a regular polygon is `160^(@)`. Find the interior angle of another regular polygon whose number of sides is two-thirds the number of sides of the given polygon.
View SolutionIf the difference between an exterior angle of a regular polygon of 'n' sides and an exterior angle of another regular polygon of `'(n+1)'` sides is equal to `5^(@)`, find the value of 'n'.
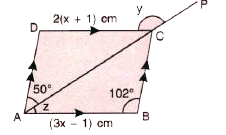
View SolutionIn the given figure, ABCD is a parallelogram. Find the values of x, y and z
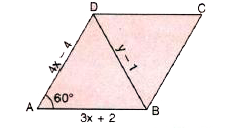
View SolutionThe given figure shows a rhombus ABCD. Find x and y
View SolutionABCD is a parallelogram and AP and CQ are perpendiculars from vertices A and C on diagonal BD . Show that(i) `DeltaA P B~=\ DeltaC Q D`(ii) `A P\ =\ C Q`
View SolutionABCD is a parallelogram and AP and CQ are perpendiculars from vertices A and C on diagonal BD . Show that(i) `DeltaA P B~=\ DeltaC Q D`(ii) `A P\ =\ C Q`
View SolutionIn the adjoining figure, ABCD and PBCQ are parallelogram. Prove that:
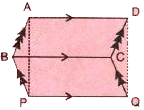
APQD is a parallelogram
View SolutionIn the adjoining figure, ABCD and PBCQ are parallelogram. Prove that:

AP= DQ
View SolutionIn the adjoining figure, ABCD and PBCQ are parallelogram. Prove that:

`Delta ABP ~= Delta DCQ`
View SolutionA transversal cuts two parallel lines PQ and RS at points A and B respectively. The two interior angles at A are bisected and so are the two interior angles at B, the four bisectors form a quadrilateral ACBD. Prove that:
ACBD is a rectangle
View Solution`A B C D` is a rhombus, `E A B F` is a straight line such that `E A=A B=B F` . Prove that `E D` and `F C` when produced meet at right angles.
View SolutionABCD is a parallelogram E is mid-point of AB and DE bisects angle D. Prove that

BC= BE
View SolutionABCD is a parallelogram E is mid-point of AB and DE bisects angle D. Prove that
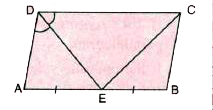
CE bisects angle C
View SolutionABCD is a parallelogram E is mid-point of AB and DE bisects angle D. Prove that

`angleDEC= 90^(@)`
View SolutionThe figure, given alongside, shows a trapezium ABCD in which AB/DC and AD= BC. Prove that:
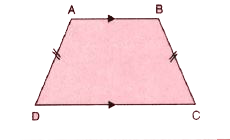
`angleA= angleB`
View SolutionThe figure, given alongside, shows a trapezium ABCD in which AB/DC and AD= BC. Prove that:
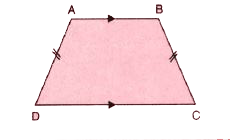
`angleC= angleD`
View SolutionThe figure, given alongside, shows a trapezium ABCD in which AB/DC and AD= BC. Prove that:
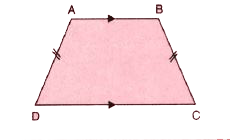
`Delta ABC ~= Delta BAD`
View SolutionThe figure, given alongside, shows a trapezium ABCD in which AB/DC and AD= BC. Prove that:
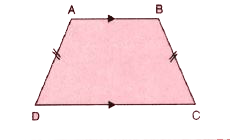
Diagonal AC= diagonal BD
View Solution
Questions questions and complete solutions for chapter RECTILINEAR FIGURES of ICSE of Class 9