Complete Solutions to TOPIC -2 ( TRIGONOMETRIC RATIOS OF STANDARD ANGLES ) (4 MARKS QUESTIONS ) of chapter TRIGONOMETRY of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | TRIGONOMETRY |
| OSWAL | TOPIC -2 ( TRIGONOMETRIC RATIOS OF STANDARD ANGLES ) (4 MARKS QUESTIONS ) |
| Number Of Questions | 8 |
| Academic Year | 2023-24 |
Prove that :
(i) `((tan 60^(@)+1)/(tan 60^(@) - 1))^(2) = (1 + cos 30^(@))/(1 - cos 30^(@))`
(ii) `3 "cosec"^(2) 60^(@) - 2 cot^(2) 30^(@) + sec^(2) 45^(@) = 0`
View SolutionProve that :
(i) `sin 60^(@) = 2 sin 30^(@) cos 30^(@)`
(ii) `4(sin^(4) 30^(@) + cos^(4) 60^(@)) - 3(cos^(2)45 - sin^(2)90^(@)) = 2`
View SolutionEvaluate :
(i) `(cos 3A - 2 cos 4A)/(sin 3 A + 2 sin 4A)`, when `A = 15^(@)`
(ii) `(3 sin 3B + 2 cos(2B + 5^(@)))/(2 cos 3B - sin(2B - 10^(@)))`, when `B = 20^(@)`
View SolutionIf `A = 30^(@)`, show that :
(i) `(1 + sin 2A + cos 2A)/(sin A + cos A) = 2 cos A`
(ii) `(cos^(3)A - cos 3A)/(cos A) + (sin^(3)A + sin 3A)/(sin A) = 3`
View SolutionCalculate the value of A, if :
(i) `(tan A - 1).("cosec 3A" - 1) = 0`
(ii) `cos 3A.(2 sin 2A - 1) = 0`
View SolutionFrom the given figure, find :
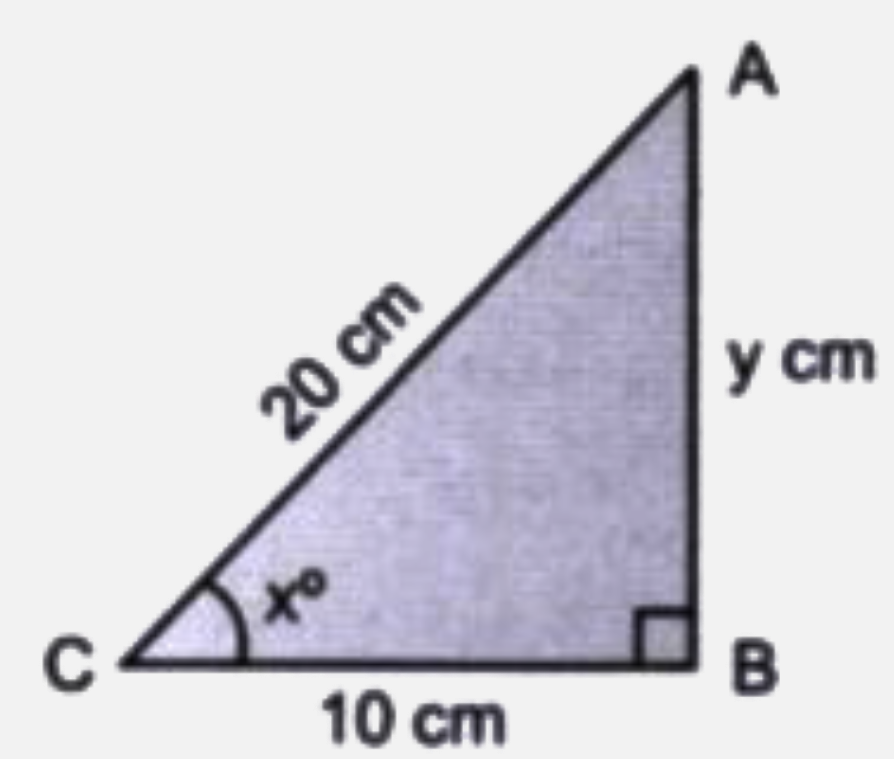
(i) `cos x^(@)`
(ii) `x^(@)`
(iii) `(1)/(tan^(2)x^(@)) - (1)/(sin 2x^(@))`
(iv) use `tan x^(@)`, to find the value of y
View SolutionFind the magnitude of angle A, if :
(i) `2 cos^(2)A - 3 cos A + 1 = 0`
(ii) `2 tan 3A cos 3A - tan 3A + 1 = 2 cos 3A`
View SolutionIf `4 cos^(2) x = 3 and x` is an acute angle find the value of :
(i) x
(ii) `cos^(2)x + cot^(2)x`
(iii) cos 3x
(iv) sin 2x
View Solution
TOPIC -2 ( TRIGONOMETRIC RATIOS OF STANDARD ANGLES ) (4 MARKS QUESTIONS ) questions and complete solutions for chapter TRIGONOMETRY of ICSE of Class 9
All Exercises from OSWAL Class 9 MATHS TRIGONOMETRY
- TOPIC -1 ( TRIGONOMETRIC RATIOS ) (3 MARKS QUESTIONS )
- TOPIC -1 ( TRIGONOMETRIC RATIOS ) (4 MARKS QUESTIONS )
- TOPIC -2 ( TRIGONOMETRIC RATIOS OF STANDARD ANGLES ) (3 MARKS QUESTIONS )
- TOPIC -2 ( TRIGONOMETRIC RATIOS OF STANDARD ANGLES ) (4 MARKS QUESTIONS )
- TOPIC -3 ( SOLUTION OF RIGHT TRIANGLES ANGLES ) (3 MARKS QUESTIONS )
- TOPIC -3 ( SOLUTION OF RIGHT TRIANGLES ANGLES ) (4 MARKS QUESTIONS )
- TOPIC -4 ( COMPLEMENTARY ANGLES ) (3 MARKS QUESTIONS )
- TOPIC -4 ( COMPLEMENTARY ANGLES ) (4 MARKS QUESTIONS )