Complete Solutions to Skill Testing Exercise of chapter NUMBER SYSTEMS of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | NUMBER SYSTEMS |
| KUMAR PRAKASHAN | Skill Testing Exercise |
| Number Of Questions | 65 |
| Academic Year | 2023-24 |
Find the rational numbers between `(3)/(5) and ( 7)/( 8)` .
View SolutionFind the rational numbers between `(1)/( 6) and ( 1)/(5) `.
View SolutionFind the rational numbers between ` (3)/(7) and (5)/(7) `
View SolutionFind the rational numbers between ` (2)/( 9) and ( 2)/( 7) `.
View SolutionFind the rational numbers between ` ( 2)/ (7) and (3)/(4)`
View SolutionLocate ` sqrt 3` on the number line.
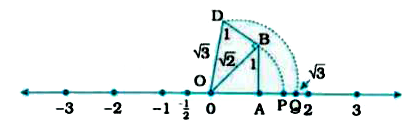
View SolutionRepresent `sqrt(17) ` on the number line
View SolutionRepresent ` sqrt(13) ` on the number line
View SolutionExpress the following number in the `(p)/(q) ` form. Where p and q are integers and ` q ne 0, `
(1) ` 0.bar4`
(2) ` 0. bar( 4.3) `
(3) ` 0. bar ( 547) `
View SolutionExpress the following number in the `(p)/(q) ` form. Where p and q are integers and ` q ne 0, `
` 0. bar( 64)`
View SolutionExpress the following number in the `(p)/(q) ` form. Where p and q are integers and ` q ne 0, `
` 0. bar(752) `
View SolutionExpress the following number in the `(p)/(q) ` form. Where p and q are integers and ` q ne 0, `
` 1. bar( 34)`
View SolutionExpress the following number in the `(p)/(q) ` form. Where p and q are integers and ` q ne 0, `
` 1. bar (27)`
View SolutionExpress the following number in the `(p)/(q) ` form. Where p and q are integers and ` q ne 0, `
` 2. bar (8) `
View SolutionExpress the following number in the `(p)/(q) ` form. Where p and q are integers and ` q ne 0, `
` 3. bar (52) `
View SolutionExpress the following number in the `(p)/(q) ` form. Where p and q are integers and ` q ne 0, `
` 4. bar ( 05) `
View SolutionExpress the following number in the `(p)/(q) ` form. Where p and q are integers and ` q ne 0, `
` 3. bar (68) `
View SolutionExpress the following number in the `(p)/(q) ` form. Where p and q are integers and ` q ne 0, `
` 2. bar (576) `
View SolutionObtain the decimal expansion of the following numbers :
` ( 4)/(11) `
View SolutionObtain the decimal expansation of the following numbers :
` ( 5)/(7)`
View SolutionObtain the decimal expansation of the following numbers :
` (37)/( 110)`
View SolutionFind an irrational number between `(3)/(7) and (4)/(7) `.
View SolutionSolve : ` 0.bar( 45) + 0.bar (23) `
View SolutionSolve : ` 0. bar ( 36) + 0. bar (28) `
View SolutionVisualize 4.287 on the number line using successive magnification.
View SolutionVisualize `5.bar(37) ` up to 4 decimal places on the number line using successive magnifications.
View SolutionVisualise `2.bar ( 63) ` up to 4 decimal places on the number line using seccessive magnifications.
View SolutionSimplify : ` 5sqrt ( 8) - 2 sqrt( 32) - 2sqrt2`
View SolutionSimplify : `( 4sqrt3 - 3sqrt5)^(2) `
View SolutionIf the `sqrt2 =1.4142 ` find the values of ` (1)/( sqrt2+ 1) `
View SolutionRationalise the denominator of each of the following expressions :
`(16)/( sqrt( 41- 5))`
View SolutionRationalise the denominator of `(1)/( 2+sqrt3)`
View SolutionRationalise the denominator of each of the folloowing expressions :
` ( 30 )/( 5sqrt3- 3sqrt5) `
View SolutionRationalize the denominator of each of the following expressions :
` (6-4sqrt2)/( 6+4sqrt2)`
View SolutionRationalize the denominator of each of the following expressions :
` (1)/( 7+3sqrt2)`
View SolutionRationalize the denominator of each of the following expressions :
` ( b^(2))/(sqrt(a^(2) +b^(2)+a))`
View SolutionRationalize the denominator and simplify:
` (sqrt3-sqrt2)/( sqrt3+sqrt2) `
View SolutionRationalize the denominator and simplify:
` (4sqrt3+5sqrt2)/( 4sqrt3+3sqrt2) `
View SolutionRationalize the denominator and simplify:
` (2sqrt6-sqrt5)/( 3sqrt5-2sqrt6) `
View SolutionIf the ` x= 8+ 3sqrt7 ` , find the value of ` x^(2) + (1)/(x^(2))` .
View SolutionIf the ` x= 5 +2sqrt6 ` find the value of ` x^(2) + (1)/(x^(2)) and x^(3) + (1)/(x^(3))`
View SolutionIf `p= (sqrt3- sqrt2) /( sqrt3+ sqrt2) and q= (sqrt3+sqrt2)/( sqrt3- sqrt2) `, find the value of ` p^(2) +q^(2)`.
View SolutionIf ` x= 2 +sqrt3. ` find the value of `x^(3) +(1)/(x^(3))`
View SolutionIf ` x = 4 +sqrt(15) `. Find the value of ` x^(2) +(1)/(x^(2)) and x^(3) + ( 1)/(x^(3))`
View SolutionSimplify :
` (3sqrt2-2sqrt3)/( 3sqrt2+2sqrt3) +(sqrt(12))/( sqrt3- sqrt2)`
View SolutionSimplify :
` (2)/(sqrt5+ sqrt3) + (1)/(sqrt3+sqrt2) - (3)/(sqrt5+sqrt2) `
View SolutionSimplify
` (sqrt5-2)/( sqrt5+2) - (sqrt 5+2)/( sqrt5-2)`
View SolutionSimplify :
` (5+sqrt3)/(7- 4sqrt3) -(5-sqrt3)/( 7+4sqrt3)`
View SolutionIf ` a + 8 sqrt5 b = ( 8+ sqrt5)/( 8- sqrt5) , ` find `a` and `b` ,
View SolutionFind the values of a and b . If
` (2sqrt6-sqrt5)/( 3sqrt5-2sqrt6)= a +b sqrt(30 ) `
View SolutionFind a and b , if ` (4+ sqrt2)/( 2+sqrt2) = a- bsqrtb.`
View SolutionFind a and b . If ` (4+ sqrt5)/( 2+sqrt5) = a+bsqrt5.`
View SolutionRepresent `sqrt(5) ` on the number line.
View SolutionIf `x= 5` and `y=2` find the values of : ` (x^(y)+ y^(x) ) `
View SolutionIf `x= 5` and `y=2` find the values of : ` (x^(x) + y^(y)) ^(-1)`
View SolutionSimplify : `[ 5^(2) (8^((1)/(3)) +27^((1)/(3)) )^(3) ]^((1)/(5))`
View SolutionEvaluate : ` ( -(1)/(27)) ^(-(2)/(3))`
View SolutionEvaluate : `3(40)^(1/3)-4 (320)^(1/3)-(5)^(1/3)`
View SolutionSimplify : ` ((25)^((3)/(2)) xx ( 343 )^((1)/(5)))/( 16^((5)/(4)) xx 8^((4)/(3)) xx 7^((3)/(5)))`
View SolutionEvaluate : ` ((64)/( 125))^(-(2)/(3)) +(1)/(((256)/(625) ) ^((1)/(4)))+ ( sqrt(25))/(" ^(3) sqrt(64))`
View SolutionIf `a =( sqrt3) /( 7)` and `(7)/(a) = bsqrt3 ` , then find the value of `b` .
View SolutionIf ` (4)^(2x- 1) - (16)^(x-1) = 384. ` find the value of `x` .
View SolutionProve that the result :
` ((2^(a) )/( 2^(b)) ) ^(a+b) xx( (2^(b))/( 2^(c))) ^(b+c) xx( (2^(c))/( 2^(a)))^(c+a)=1`
View SolutionWrite the following in the ascending order of their magnitude:
` sqrt 3 , " " ^(3) sqrt4 , " " ^(4) sqrt( 6) `
View SolutionIf ` ((3)/(4))^(6) xx((16)/( 9)) ^(5)= ((4)/( 3) ) ^(x+2)` find the value of x.
View Solution
Skill Testing Exercise questions and complete solutions for chapter NUMBER SYSTEMS of KUMAR PRAKASHAN KENDRA MATHS (GUJRATI ENGLISH) of Class 9