Complete Solutions to Skill Testing Exercise of chapter LINE AND ANGLES of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | LINE AND ANGLES |
| KUMAR PRAKASHAN | Skill Testing Exercise |
| Number Of Questions | 21 |
| Academic Year | 2023-24 |
`angleA` and `angleB` are supplementary angles. If `angleA=x+10^(@)` and `angleB=x-10^(@)`, find `angleA` and `angleB`.
View Solution`angleA` and `angleB` are supplementary angles. If `angleA:angleB=7:8`, find `angleA` and `angleB`.
View Solution`angleA` and `angleB` are complementary angles. If `angleA=x+20^(@)` and `angleB=x-10^(@)`, find `angleA` and `angleB`.
View Solution`angleA` and `angleB` are complementary angles. If `angleA=angleB+20^(@)`, find `angleA` and `angleB`
View Solution`angleX` and `angleY` are supplementary angles. If `angleX=5 angleY`, find `angleX` and `angleY`.
View Solution`angleP` and `angleQ` are supplementary angles. If `angleP=angleQ-40^(@),` find `angleP` and `angleQ`
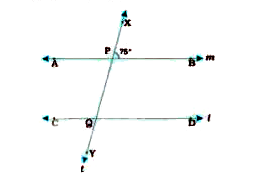
View SolutionIn the following figure, l II m and t is their transversal. If `angleXPB=75^(@)`, find `anglePQD,angleCQY` and `angleAPQ`
View SolutionIn the following l II m and t is their transversal. If `angleAXY=65^(@)`, find `angleBYF,angleXYD,angleEXC` and `angleYXC`.

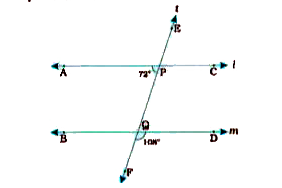
View SolutionIn the following figure, t is the transversal of l and m. If `angleAPQ=72^(@)` and `angleDQF=108^(@)` , prove that `l||m`.
View SolutionRay AX is the bisector of `angleBAC` and ray AY is the bisector of `angleXAC`. If `angleBAY=60^(@)`, find `angleBAC`.
View SolutionRay EX is the bisector of `angleDEF` and ray EY is the bisector of `angleDEX`. If `angleDEX=42^(@)`, find `angleYEF` and `angleDEF`.
View Solution`angleX` and `angleY` are supplementary angles. If `angleX:angleY=25:11`, find `angleX` and `angleY`.
View Solution`angleA` and `angleB` are supplementary angles. If `4angleA=5angleB`, find `angleA` and `angleB`.
View SolutionIn `DeltaABC,angleA:angleB:angleC=3:4:5`. Find the measure of each angle of `DeltaABC`.
View SolutionIn `DeltaABC,angleA=(angleB+angleC)/(3)` and `angleB:angleC=2:1`.
Find the measure of each angle of `DeltaABC` and state the type of `DeltaABC`.
View SolutionSide BC of `DeltaABC` is extended on both the sides so that exterior angles `angleABD` and `angleACE` are formed. If `angleABD=90^(@)` and `angleACE=130^(@)`, find the measure of each angle of `DeltaABC`.
View Solution`angleACD` is an exterior angle of `DeltaABC` and he bisector of `angleA` intersects BC at E. Prove that, `angleABC+angleACD=2angleAEC`.
View SolutionFor the figure given below, prove that `angleADC=angleA+angleB+angleC`.

View SolutionIn `DeltaABC`, the bisectors of `angleB` and `angleC` intersect each other at O. Prove that. `angleBOC=90^(@)+(1)/(2)angleA`.
View SolutionFor the figure below, prove that `angleCBE+angleADF=angleDAB+angleDCB`.

View SolutionProve that the sum of angles of any convex quadrilateral is `360^(@)`.
View Solution
Skill Testing Exercise questions and complete solutions for chapter LINE AND ANGLES of KUMAR PRAKASHAN KENDRA MATHS (GUJRATI ENGLISH) of Class 9