Complete Solutions to EXERCISE 10.5 of chapter CIRCLES of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | CIRCLES |
| KUMAR PRAKASHAN | EXERCISE 10.5 |
| Number Of Questions | 12 |
| Academic Year | 2023-24 |
In the given figure, A, B and C are three points on a circle with centre O such that `angle BOC = 30 ^(@) and angle AOB = 60^(@).` If D is a point on the circle other than the are ABC, find `angle ADC.`
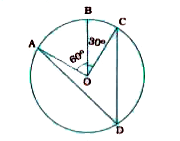
View SolutionA chord of a circle is equal to the radius of the circle. Find the angle subtended by the chord at a point on the minor arc and also at a point on the major arc.
View SolutionIn the given figure, `angle PQR = 100^(@),` where P, 9 and R are points on a circle with centre O. Find `angle OPR.`

View SolutionIn the given figure, `angle ABC = 69^(@), angle ACB= 31 ^(@),`
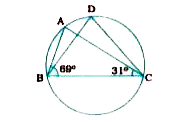
View SolutionIn the given figure, A, B, C and D are four points on a circle. AC and BD intersect at a point E such that `angle BEC = 130^(@) and angle ECD = 20^(@). ` . Find `angle BAC.`

View SolutionABCD is a cyclic quadrilateral whose diagonals intersect at a point E. If `angle DBC = 70^(@), angle BAC is 30^(@),` find `angle BCD.` Further, if AB = BC, find `angle ECD.`

View SolutionIf diagonals of a cyclic quadrilateral are diameters of the circle through the vertices of the quadrilateral, prove that it is a rectangle.

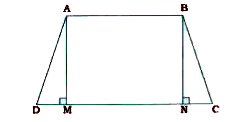
View SolutionIf the non-parallel sides of a trapezium are equal, prove that it is cyclic.
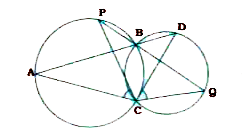
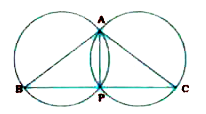
View SolutionTwo circles intersect at two points B and c. Through B, two line segments ABD and PBQ are drawn to intersect the circles at A, D and P, Q respectively (see the given figure). Prove that `angle ACP = angle QCD.`
View SolutionIf circles are drawn taking two sides of a triangle as diameters, prove that the point of intersection of these circles lie on the third side.
View SolutionABC and ADC are two right triangles with common hypotenuse AC. Prove that `angle CAD = angle CBD.`
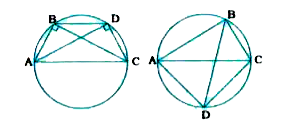
View SolutionProve that a cyclic parallelogram is a rectangle.
View Solution
EXERCISE 10.5 questions and complete solutions for chapter CIRCLES of KUMAR PRAKASHAN KENDRA MATHS (GUJRATI ENGLISH) of Class 9