Complete Solutions to प्रश्नावली 8(C) of chapter चतुर्भुज of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | चतुर्भुज |
| MANOHAR RAY | प्रश्नावली 8(C) |
| Number Of Questions | 13 |
| Academic Year | 2023-24 |
एक चतुर्भुज के कोण `3:5:9:13` के अनुपात में हैं। इस चतुर्भुज के सभी कोण ज्ञात कीजिए।
02:49View Solutionयदि एक समांतर चतुर्भुज के विकर्ण बराबर हो, तो दर्शाइए कि वह एक आयत है।
02:58View Solutionदर्शाइए कि यदि एक चतुर्भुज के विकर्ण परस्पर समकोण पर समद्विभजित करे , तो वह एक समचतुर्भुज होता है ।
07:31View Solutionदर्शाइए कि एक वर्ग के विकर्ण बराबर होते है और परस्पर समकोण पर समद्विभजित करते है ।
14:44View Solutionसमलंब चतुर्भुज
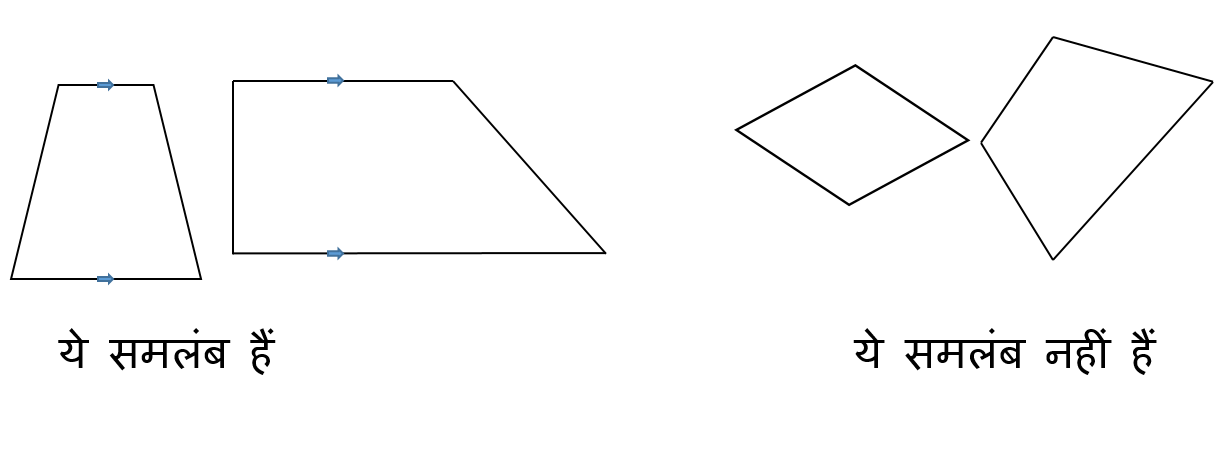
समलंब चतुर्भुज एक ऐसा चतुर्भुज होता हैं जिसमे भुजाओं का एक युग्म समांतर होता हैं तथा दूसरा युग्म समांतर नहीं होता हैं |
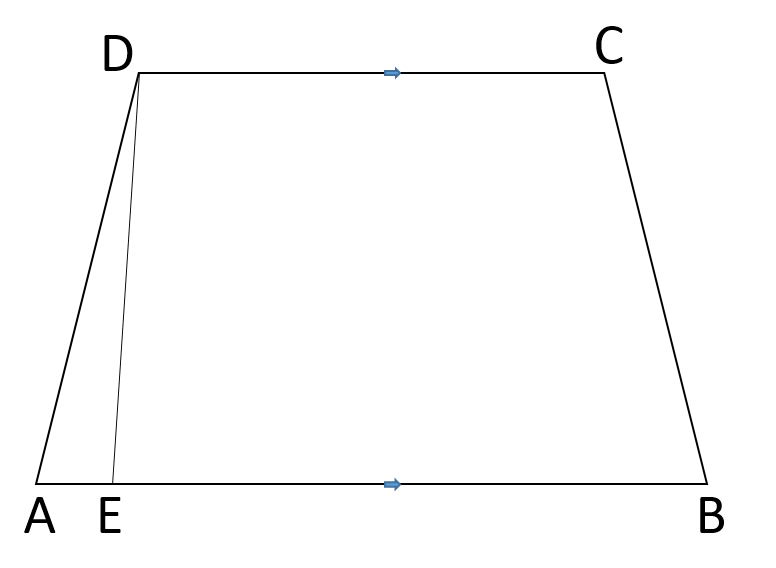
(i) चित्र में दिये गये तीर का निशान समांतर भुजाओं को दर्शाते हैं।
(ii) `DE` समलम्ब चतुर्भुज की ऊँचाई है।
पतंग
पतंग एक चतुर्भुज होता है जिसकी आसन्न भुजाओं के युग्म आपस में बराबर होती हैं। उदाहरण `AB = AD` और `BC = CD`
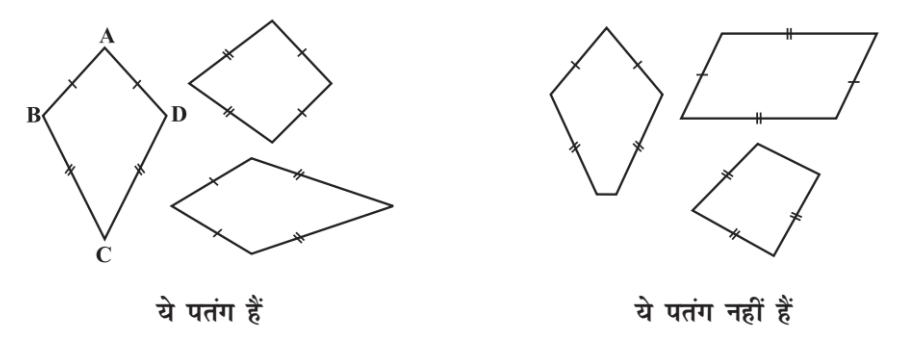
(i) एक पतंग में चार भुजायें होती हैं |
(ii) इनमे अलग - अलग आसन्न भुजाओं के दो युग्म होते हैं | जिनकी लंबाई बराबर होती हैं ।
(iii) पतंग के विकर्ण एक दूसरे पर लम्ब होते हैं ।समांतर चतुर्भुज
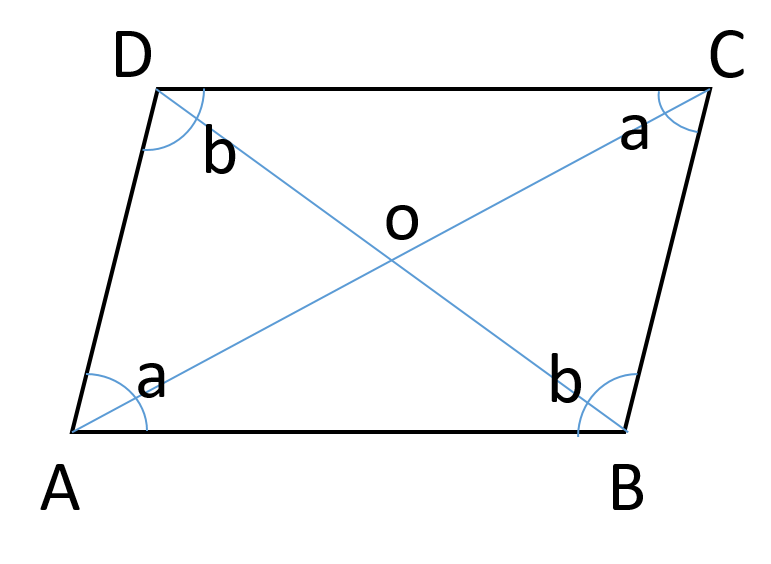
चतुर्भुज, जिसकी आमने सामने की भुजाएँ समांतर हों, उसे समांतर चतुर्भुज कहते हैं। जैसे - चित्र में `AB = CD` और `AD = BC` हैं|
समांतर चतुर्भुज के गुण
दिये गये समांतर चतुर्भुज `ABCD` में
कोण `A = ` कोण `C` और कोण `B = ` कोण `C`
भुजा `AB =` भुजा `DC` और भुजा `AD =` भुजा `BC`
`OA = OC` और `OB = OD`
कोण `A` `+` कोण `D` `= 180^@`
और कोण `A +` कोण `B = 180^@`
और कोण `B +` कोण `C = 180^@`
और कोण `C +` कोण `D` `= 180^@`
(a) समांतर चतुर्भुज की आमने सामने की भुजाएँ (सम्मुख भुजाएँ) समानांतर होती हैं।
(b) समांतर चतुर्भुज की आमने सामने की भुजाएँ (सम्मुख भुजाएँ) आपस में बराबर होती हैं।
(c) समांतर चतुर्भुज के आमने सामने के कोण (सम्मुख कोण) आपस में बराबर होते हैं।
(d) समांतर चतुर्भुज में आसन्न कोण सम्पूरक होते हैं। अर्थात समांतर चतुर्भुज के दो आसन्न कोणों का योग `180^@` होता है।
(e) समांतर चतुर्भुज के विकर्ण एक दूसरे को दो बराबर भागों में बाँटते हैं।
(f) समांतर चतुर्भुज का क्षेत्रफल `= 1/2 xx` आधार `xx` ऊँचाई
(g) समांतर चतुर्भुज का क्षेत्रफल `= 1/2 xx `विकर्णों का गुणनफल
(g) समांतर चतुर्भुज का परिमाप `= 2` ( आधार + आधार की आसन्न भुजा )05:34View Solutionसमांतर चतुर्भुज ABCD का विकर्ण AC कोण A को समद्विभाजित करता है। दर्शाइ कि
(i) यह `/_C` का भी समद्विभाजित करता है।
(ii) ABCD एक समचतुर्भुज है।
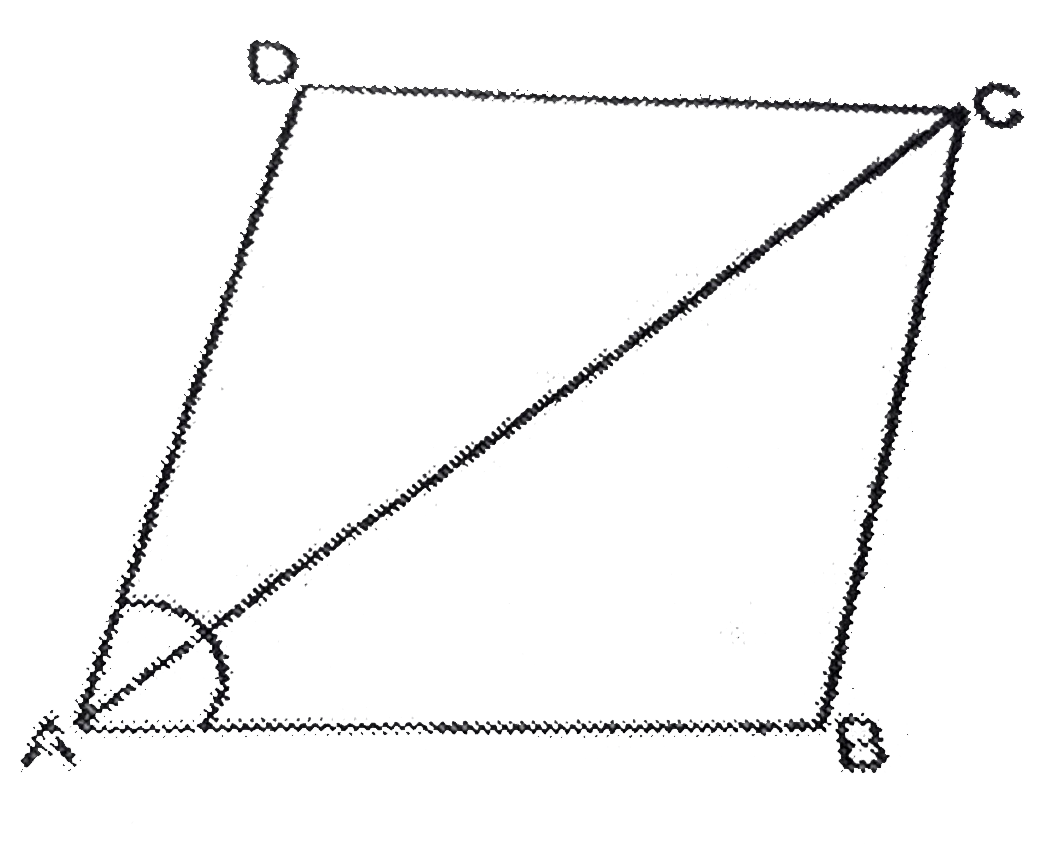
05:50View Solution`ABCD` एक एमचतुर्भुज है। दर्शाइए कि विकर्ण AC कोणों A और C दोनों को समद्विभाजित करता है तथा विकर्ण BD कोणों B और D दोनों का समद्विभाजित करता है।
04:34View Solution`ABCD` एक आयत है जिसमें विकर्ण AC दोनों कोणों A और C को समद्विभाजित करता हैं दर्शाइए कि (i) ABCD एक वर्ग है (ii) विकर्ण BD दोनों कोणों B और D को समद्विभाजित करता है।
05:04View Solution`ABCD` एक समांतर चतुर्भुज है तथा AP और CQ शीर्षों A और C से विकर्ण BD पर क्रमशः लम्ब है। दर्शाइए कि
(i) `DeltaAPB~=DeltaCQD`
(ii) `AP=CQ`
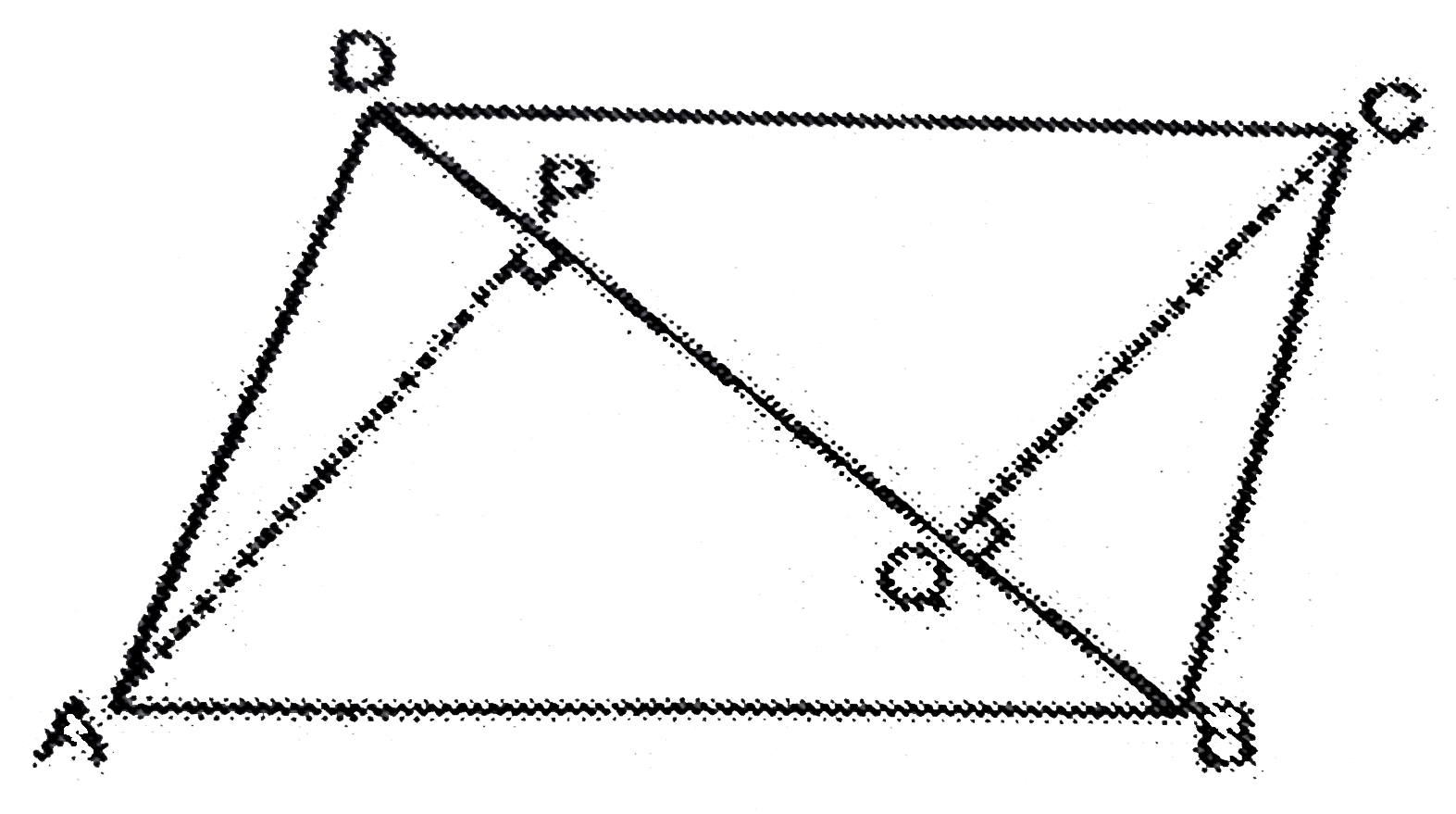
03:45View Solutionसिद्ध कीजिए कि एक वर्ग की भुजाओं के मध्य बिंदुओं को मिलाकर बनाया गया चतुर्भुज एक वर्ग ही है।
12:34View Solutionएक चतुर्भुज ABCD से विकर्ण परस्पर लम्ब है। सिद्ध कीजिए कि इसकी भुजाओं के मध्य बिंदुओं को मिलाने वाले रेखाखण्डों से एक आयत बनता है।
04:22View Solutionसिद्ध कीजिए कि समांतर चतुर्भुज ABCD में A व B पर बने कोणों को अंतः तथा बाह्य समद्विभाजक द्वाराएक आयत बनता है।
04:53View Solutionसिद्ध कीजिए आयत की संलग्न भुजाओं के मध्य बिंदुओं को मिलाने से निर्मित चतुर्भुज समचतुर्भुज होता है।
03:14View Solution
प्रश्नावली 8(C) questions and complete solutions for chapter चतुर्भुज of DR MANOHAR RAY MATHS (HINDI) of Class 9