Complete Solutions to EXAMPLE of chapter NEW NUMBERS of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | NEW NUMBERS |
| MAXIMUM PUBLICATION | EXAMPLE |
| Number Of Questions | 36 |
| Academic Year | 2023-24 |
In the picture, the square on the hypotenuse of the top most right triangle Is drawn. Calculate the area and the length of a side of the square.
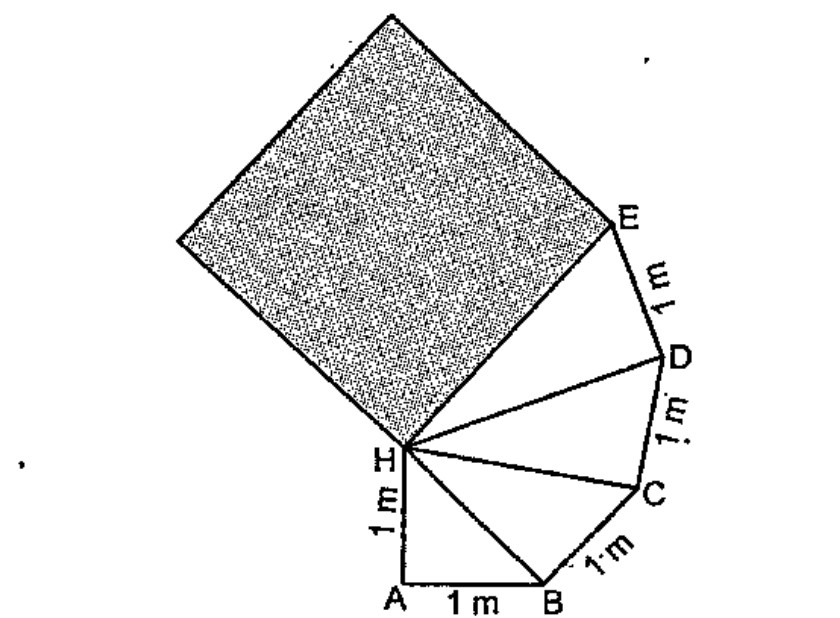 .
.
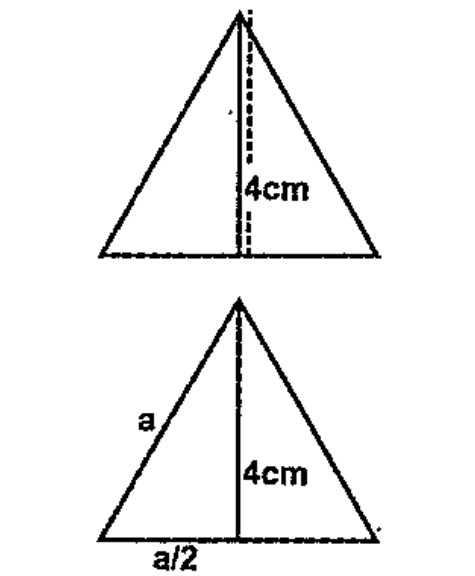
View SolutionA square is drawn on the altitude of an equilateral triangle of side 2 metres.
What is the area of the square?
 .
.
View SolutionWe have seen in class 7 that any odd number can be written as the difference of two perfect squares. (The lesson identities) Using this, drawn lines of length `sqrt7` and `sqrt11` centimetres.
View SolutionExplain two different method of drawing a line of lengths `sqrt13` centimetres.
View SolutionFind three fractions larger than `sqrt2` and less than `sqrt3`.
View SolutionThe hypotenuse of a right triangle is `1frac(1)(2)` metres and another side is `frac(1)(2)` metre.Calculate the perimeter correct to a centimetre.

View SolutionThe picture shows an equilateral triangle cut into halves by a line through a vertex.
What is the perimeter of a part?
 .
.
View SolutionThe picture shows an equilateral triangle cut into halves by a line through a vertex.
How much less than the perimeter of the whole triangle is this?
 .
.
View SolutionCalculate the perimeter of the triangle shown below.
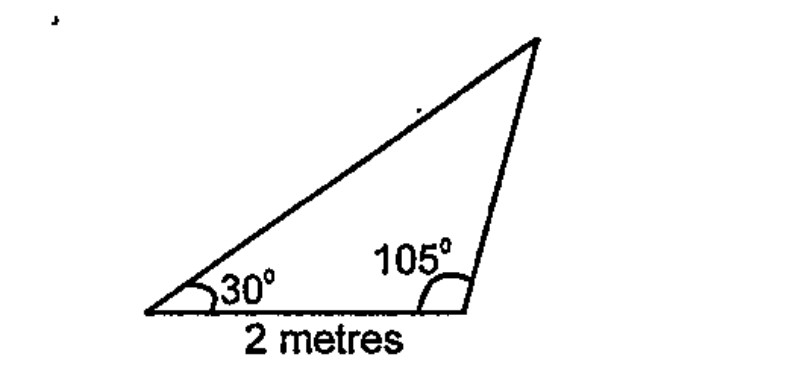 .
.
View SolutionWe have seen how we can draw a series of right triangles as in the picture.
What are the lengths of the sides of the tenth triangle?
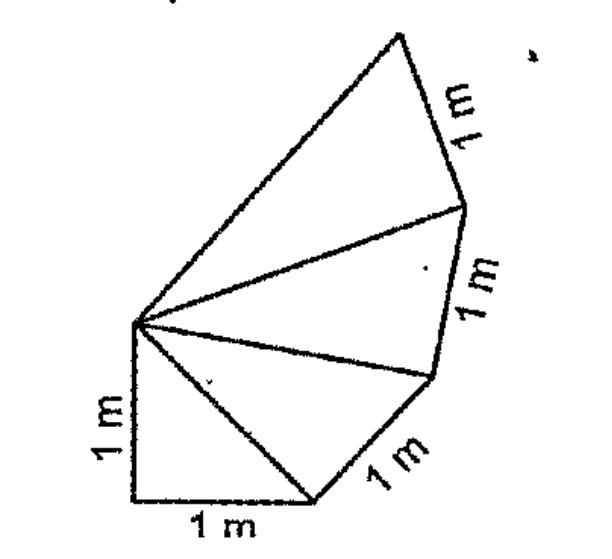 .
.
View SolutionWe have seen how we can draw a series of right triangles as in the picture.
How mulch more is the perimeter of the `10^th` triangle than the perimeter of the ninth triangle?
 .
.
View SolutionWe have seen how we can draw a series of right triangles as in the picture.
How do we write in algebra, the difference in perimeter of the nth triangle to that of the triangle just before it?
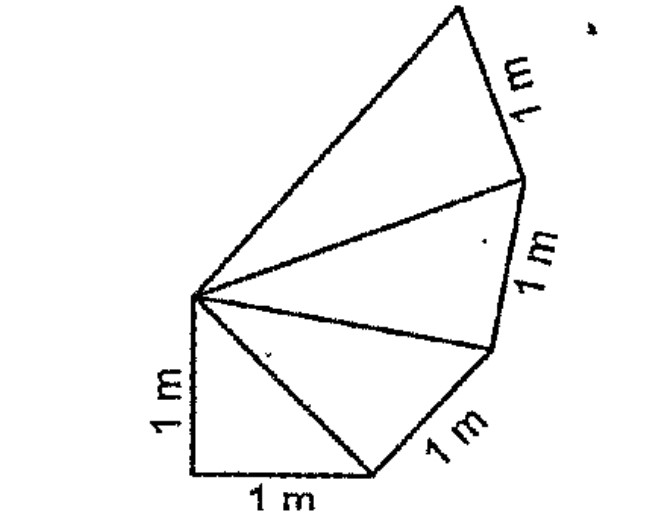 .
.
View SolutionWhat is the hypotenuse of the right triangle with perpendicular sides `sqrt2`centimeteres and `sqrt3` centimeters? How much larger than the hypotenuse is the sum of the perpendicular sides?
View SolutionOf four equal equilateral triangles two are cut vertically into halves and two whole are put together to make a rectangle.
Area and perimeter of the rectangle.
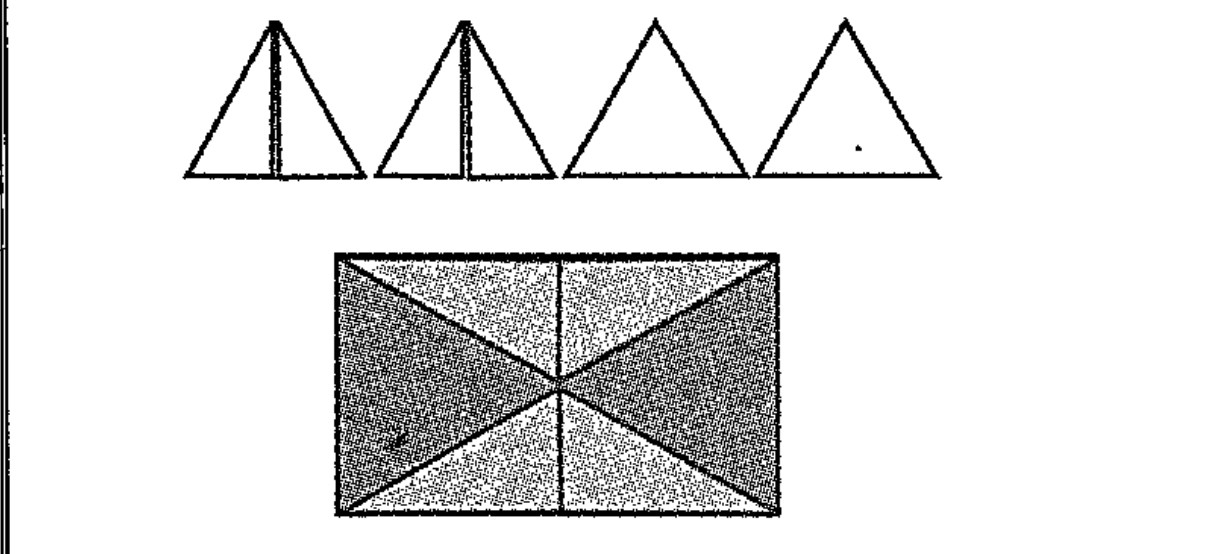 .
.
View SolutionA square and equiIateral triangle of sides twice as long we cut and the pieces are rearranged to form a trapezium, as shown below.
If a side of the square is 2 centimetres, what are the perimeter and area of the trapezium?
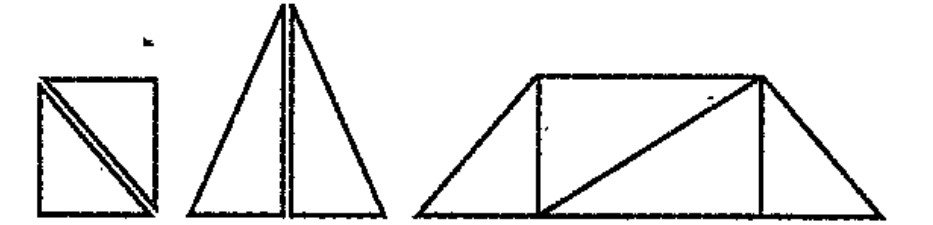 .
.
View SolutionFrom the pairs of numbers given below, pick out those whose product is a natural number or a fraction.
`sqrt3`,`sqrt12`.
View SolutionFrom the pairs of numbers given below, pick out those whose product is a natural number or a fraction.
`sqrt3`,`sqrt1.2`.
View SolutionFrom the pairs of numbers given below, pick out those whose product is a natural number or a fraction.
`sqrt5`,`sqrt8`.
View SolutionFrom the pairs of numbers given below, pick out those whose product is a natural number or a fraction.
`sqrt0.5`,`sqrt8`.
View SolutionFrom the pairs of numbers given below, pick out those whose product is a natural number or a fraction.
`sqrt(7frac(1)(2))`,`sqrt(3frac(1)(3))`.
View SolutionCalculate the length of the sides of the equilateral triangle on the right correct to a millimeter.
 .
.
View SolutionProve that `(sqrt2+1)(sqrt2-1)=1`. Use this to compute `frac(1)sqrt(2-1)`.Correct two decimal places.
View SolutionCompute `frac(1)(sqrt2+1)` correct two decimal places.
View SolutionSimplify
`(sqrt3-sqrt2)(sqrt3+sqrt2)`
Using this compute
`1/(sqrt3-sqrt2)` and `1/(sqrt3+sqrt2)`.
View SolutionAll black triangles in the picture are equilateral.
What is the ratio of sides of the outer and inner squares?
 .
.
View SolutionThe hypotenuse of a right triangle is 3.5 metres long. One side is 2.5 metre. Calculate the perimeter correct to centimetres.
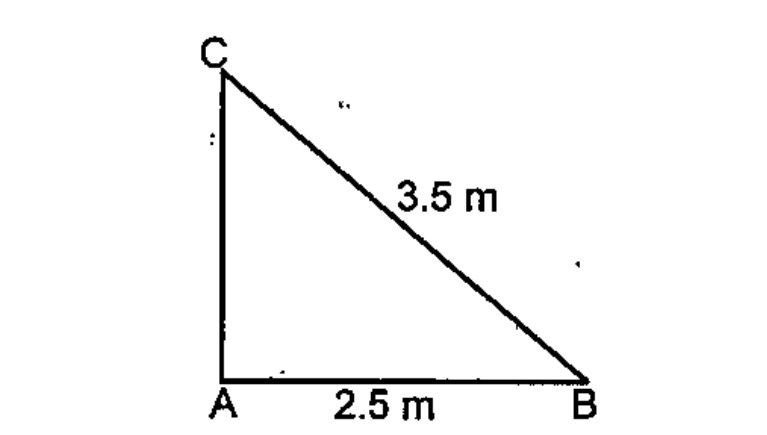 .
.
View SolutionThe sides of a square are 6 centimetres long. The mid points of the sides are joined to form another square as shown below.
What is the perimeter of the smaller square?
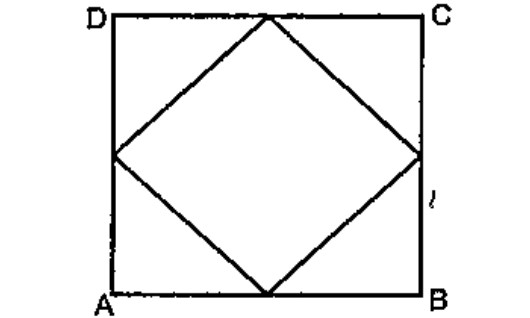 .
.
View SolutionFind the sum,`sqrt32+sqrt512+sqrt8`
View SolutionFind the value of `sqrt675-sqrt147`.
View SolutionA,B,C are three points such that `AB=sqrt75`,`BC=sqrt108`,`AC=sqrt363`.Do they lie on a straight line?
View SolutionSimplify
`5/(2sqrt7-3sqrt5)`
(Given`sqrt7=2.646`,`sqrt5=2.23`)
View SolutionFind the value of 'a' , if `sqrt80+sqrt180+asqrt5=0`.
View SolutionFind the rational numbers between `1/5` and `1/6`.
View SolutionIf the two sides of a right angled triangle other than the hypotenuse are 12 cm and 10 cm: Find the altitude to the hypotenuse.
View SolutionSimply, `33/(3sqrt5+2sqrt3)`.
View SolutionGiven, `sqrt3=1.73`.Find the approximate value of `2/(3sqrt3)+5/sqrt27` into two decimals places.
View Solution
EXAMPLE questions and complete solutions for chapter NEW NUMBERS of MAXIMUM PUBLICATION of Class 9