Complete Solutions to EXAMPLE of chapter SIMILAR TRIANGLES of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | SIMILAR TRIANGLES |
| MAXIMUM PUBLICATION | EXAMPLE |
| Number Of Questions | 13 |
| Academic Year | 2023-24 |
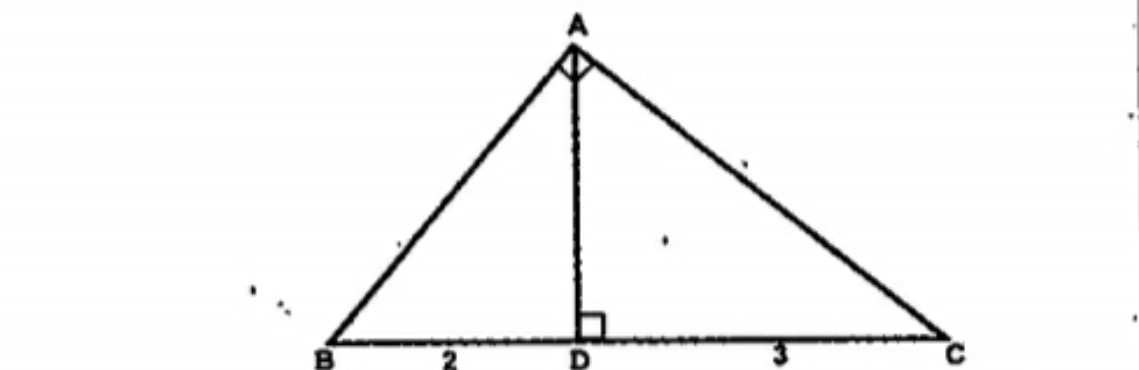
The perpendicular from the square corners of a right angle triangle cuts the opposite side into two parts of 2 and 3 cm length.Prove that two small triangles cut by the perpendicular have the same angles.
View SolutionThe perpendicular from the square corners of a right angle triangle cuts the opposite side into two parts of 2 and 3 cm length. Taking the length of the perpendicular as h, prove that `h/2=3/h`
View SolutionThe perpendicular from the square corners of a right angle triangle cuts the opposite side into two parts of 2 and 3 cm length. Calculate the perpendicular sides of the large triangle.
View SolutionThe perpendicular from the square comers of a right triangle cuts the opposite side into two parts of 2 and 3 cm length.
Prove that if the perpendicular from the square corner of the right triangle divides the opposite sides into partsof length a and b and if the length of the perpendicular is h, then `h^2= ab`
 .
.
View SolutionAt two ends of a horizontal line, angles of equal size are drawn, and two points on the slanted lines are joined. Prove that the parts of the horizontal line and parts of slanted lines are in the same ratio.
View SolutionAt two ends of a horizontal line, angles of equal size are drawn, and two points on the slanted lines are joined. Prove that the two slanted lines at the ends of the horizontal line are in the same ratio
View SolutionAt two ends of a horizontal line, angles of equal size are drawn, and two points on the slanted lines are joined. Explain how a line of length 6 cm can be divided in the ratio `3:4`
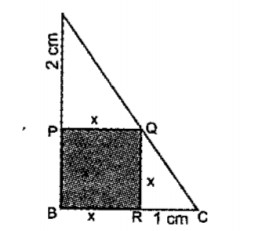
View SolutionThe picture shows a square drawn sharing one cor¬ner with a right triangle and the other three corners on the sides of this triangle.
Calculate the length of a side of the square.
 .
.
View SolutionTwo poles of height 3 m and 2m are erected upright on the ground and ropes are stretched from the top of each to the foot of the tower.
At what height above the ground do the ropes cross each other.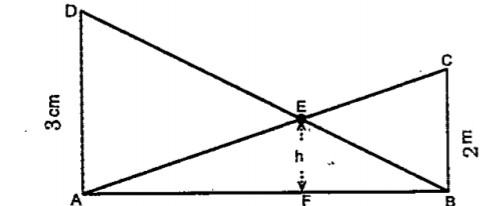 .
.
View SolutionTwo poles are erected upright on the ground and ropes are stretched from the top of each to the foot of the tower.
Taking the heights of the poles as 'a' and 'b' and height above the ground of the point where the ropes cross each other as h, find the relation between a,b and h.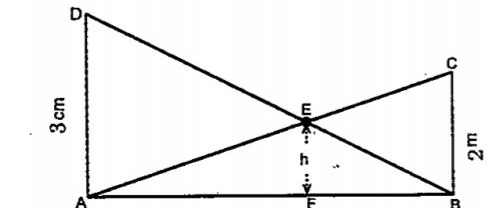 .
.
View SolutionTwo poles of height 3 m and 2m are erected upright on the ground and ropes are stretched from the top of each to the foot of the tower.
Prove that this height would be the same whatever be the distance between the poles. .
.
View SolutionThe picture shows two circles with the same centre and two triangles formed by joining the centre to the points of intersection of the circles with two radii of the larger circle.
prove that these triangles are similar
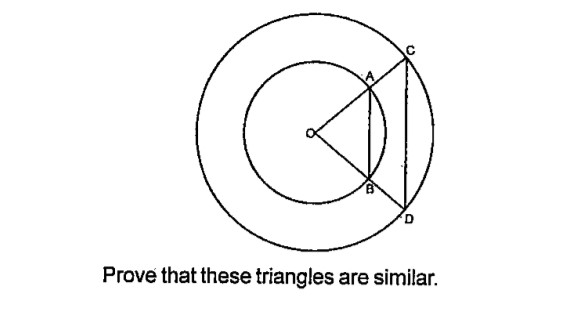 .
.
View SolutionThe lines joining the circumcentre of a Wangle to the vertices are extended to meet another circle with the same centre, and these points are joined to make another triangle.
Prove that the two triangles are similar.
 .
.
View Solution
EXAMPLE questions and complete solutions for chapter SIMILAR TRIANGLES of MAXIMUM PUBLICATION of Class 9