Complete Solutions to पाठ्य - पुस्तक प्रश्नावली 10.5 of chapter वृत्त of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | वृत्त |
| MBD-HARYANA BOARD | पाठ्य - पुस्तक प्रश्नावली 10.5 |
| Number Of Questions | 12 |
| Academic Year | 2023-24 |
आकृति में, केंद्र O वाले एक वृत्त पर तीन बिंदु A, B और C इस प्रकार है कि `angleBOC=30^(@)` तथा `angleAOB=60^(@)` हैं| यदि चाप ABC के अतिरिक्त वृत्त पर D पर एक बिंदु है, तो `angleADC` ज्ञात कीजिए |

View Solutionकिसी वृत्त की एक जीवा वृत्त की त्रिज्या के बराबर है| जीवा द्वारा लघु चाप के किसी बिंदु पर अंतरित कोण ज्ञात कीजिए तथा दीर्घ चाप के किसी बिंदु पर भी अंतरित कोण ज्ञात कीजिए |
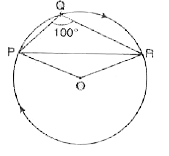
View Solutionआकृति है, `anglePQR=100^(@)` जहाँ P, Q तथा R केंद्र O वाले एक वृत्त पर स्थित हैं| `angleOPR` ज्ञात कीजिए |
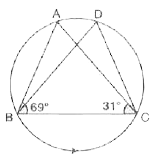
View Solutionआकृति में, `angleABC=69^(@)` और `angleACB=31^(@)` हो, तो `angleBDC` ज्ञात कीजिए |
View Solutionआकृति में, एक वृत्त पर A, B, C और D चार बिंदु हैं| AC और BD एक बिंदु E पर एक प्रकार प्रतिच्छेद करते हैं कि `angleBEC=130^(@)` और `angleECD=20^(@)` हैं| `angleBAC` ज्ञात कीजिए |
View SolutionABCD एक चक्रीय चतुर्भुज है जिसके विकर्ण एक बिंदु E पर प्रतिच्छेद करते हैं| यदि `angleDBC=70^(@)` और `angleBAC=30^(@)` हो, तो `angleBCD` ज्ञात कीजिए | पुनः यदि `AB=BC` हो, तो `angleECD` ज्ञात कीजिए |
View Solutionयदि एक चक्रीय चतुर्भुज के विकर्ण उसके शीर्षों से जाने वाले वृत्त के व्यास हों, तो सिद्ध कीजिए कि वह एक आयत है|
View Solutionयदि एक समलम्ब की असमान्तर भुजाएँ बराबर हैं, तो सिद्ध कीजिए कि वह चक्रीय है|
View Solutionदो वृत्त बिंदुओं B और C पर प्रतिच्छेद करते हैं | B से जाने वाले दो रेखाखण्ड ABD और PBQ वृत्तों को A, D और P, Q पर क्रमशः प्रतिच्छेद करते हुए खींचे गए हैं (देखिए आकृति )| सिद्ध कीजिए कि `angleACP=angleQCD` है|

View Solutionयदि किसी त्रिभुज की दो भुआजों को व्यास मानकर वृत्त खींचे जाएं, तो सिद्ध कीजिए कि इन वृत्तों का प्रतिच्छेद बिंदु तीसरी भुजा पर स्थित है|
View Solutionउभयनिष्ठ कर्ण AC वाले दो समकोण त्रिभुज ABC और ADC है| सिद्ध कीजिए कि `angleCAD=angleCBD` है|
View Solutionसिद्ध कीजिए कि एक चक्रीय समांतर चतुर्भुज आयत होता है|
View Solution
पाठ्य - पुस्तक प्रश्नावली 10.5 questions and complete solutions for chapter वृत्त of MBD MATHS (HINDI) of Class 9
All Exercises from MBD-HARYANA BOARD Class 9 MATHS वृत्त
- अभ्यास के लिए प्रश्न
- अभ्यास के लिए प्रश्न (अति लघु उत्तरात्मक प्रश्न)
- अभ्यास के लिए प्रश्न (दीर्घ उत्तरात्मक प्रश्न)
- अभ्यास के लिए प्रश्न (लघु उत्तरात्मक प्रश्न)
- पाठ्य - पुस्तक प्रश्नावली 10.1
- पाठ्य - पुस्तक प्रश्नावली 10.1(खाली स्थान भरिए: )
- पाठ्य - पुस्तक प्रश्नावली 10.2
- पाठ्य - पुस्तक प्रश्नावली 10.3
- पाठ्य - पुस्तक प्रश्नावली 10.4
- पाठ्य - पुस्तक प्रश्नावली 10.5
- पाठ्य - पुस्तक प्रश्नावली 10.6
- बहुविकल्पी प्रश्न
- महत्वपूर्ण उदाहरण (अति लघु उत्तरात्मक प्रश्न)
- महत्वपूर्ण उदाहरण (दीर्घ उत्तरात्मक पश्न)
- महत्वपूर्ण उदाहरण (लघु उत्तरात्मक प्रश्न)
- महत्वपूर्ण प्रश्न (उदाहरण)