Complete Solutions to Exercise of chapter Linear Equations In Two Variables of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | Linear Equations In Two Variables |
| MBD | Exercise |
| Number Of Questions | 92 |
| Academic Year | 2023-24 |
The cost of a note book is twice the cost of a pen. Write a linear equation in two variables to represent this statement.
View SolutionExpress the following linear equation in the form ax + by + c = 0 and indicate the values of a, b and c in each case. `2x+3y=9.3overline5`.
View SolutionExpress the following linear equation in the form ax + by + c = 0 and indicate the values of a, b and c in each case. `x-y/5-10=0`
View SolutionExpress the following linear equation in the form ax + by + c = 0 and indicate the values of a, b and c in each case. `-2x+3y=6`.
View SolutionExpress the following linear equation in the form ax + by + c = 0 and indicate the values of a, b and c in each case. `x=3y`.
View SolutionExpress the following linear equation in the form ax + by + c = 0 and indicate the values of a, b and c in each case. `2x=-5y`.
View SolutionExpress the following linear equation in the form ax + by + c = 0 and indicate the values of a, b and c in each case. `3x+2=0`.
View SolutionExpress the following linear equation in the form ax + by + c = 0 and indicate the values of a, b and c in each case. `y-2=0`.
View SolutionExpress the following linear equation in the form ax + by + c = 0 and indicate the values of a, b and c in each case. `5=2x`.
View SolutionWrite the following equation in the form ax + by + c = 0 and indicate the values of a, b an c in the case : `2x+3y=4`.
View SolutionWrite the following equation in the form ax + by + c = 0 and indicate the values of a, b an c in the case : `x-4=3y`.
View SolutionWrite the following equation in the form ax + by + c = 0 and indicate the values of a, b an c in the case : `6=5x-3y`.
View SolutionWrite the following equation in the form ax + by + c = 0 and indicate the values of a, b and c in the case : `2x=y`.
View SolutionWrite the following equation in the form ax + by + c = 0 and indicate the values of a, b and c in the case : `5y=x`.
View SolutionWrite the following equation in the form ax + by + c = 0 and indicate the values of a, b an c in the case : `x/3=y/5+7`.
View SolutionWrite the following equation in two variables : `x=-5`.
View SolutionWrite the following equation in two variables : `y=2`.
View SolutionWrite the following equation in two variables : `2x=3`.
View SolutionWrite the following equation in two variables : `5y=2`.
View SolutionWrite the following equation in two variables : `-3y=7`.
View SolutionWrite the following equation in two variables : `-3x=1`.
View SolutionIn One Day International cricket match between India and South Africa played in Kolkata, two Indian batsmen Rahul and Sourav together scored, 185 runs. Express this information in the form of an equation. (Take runs scored by Rahul as x and runs scored by Sourav as y).
View SolutionWhich one of the following option is true and why ? `y = 3x + 5` has
View SolutionWrite four solutions for the following equation : `2x+y=7`.
View SolutionWrite four solutions for the following equation : `pix+y=9`.
View SolutionWrite four solutions for the following equation : `x=4y`.
View SolutionCheck the following is solution of the equation `x - 2y = 4` or not. (0, 2)
View SolutionCheck the following is solution of the equation `x - 2y = 4` or not. (2, 0)
View SolutionCheck the following is solution of the equation `x - 2y = 4` or not. (4, 0)
View SolutionCheck the following is solution of the equation `x - 2y = 4` or not. `(sqrt2, 4sqrt2)`
View SolutionCheck the following is solution of the equation `x - 2y = 4` or not. (1, 1)
View SolutionFind the value of k if x = 2, y = 1 is a solution of the equation 2x + 3y = k.
View SolutionFind two solutions for the following equation : 2x + 3y = 12.
View SolutionFind two solutions for the following equation : 2x + 5 = 0.
View SolutionFind two solutions for the following equation : 3y + 4 = 0.
View SolutionFind two solutions for the following equation : 4x - y = 9.
View SolutionFind at least four solutions for the given equations: 5x + 7y = 12.
View SolutionFind at least four solutions for the given equations: 4x + 3y = 13.
View SolutionFind at least four solutions for the given equations: x + 2y = 6.
View SolutionFind at least four solutions for the given equations: `-3x + y =7`.
View SolutionFind the value of `a` so that the following equation may have `x = -4` and `y = 1` as a solution. `-5x+2ay=-8`.
View SolutionFind the value of `a` so that the following equation may have `x = -4` and `y = 1` as a solution. `-5x+2ay=-8`.
View SolutionFind the value of `a` so that the following equation may have `x = -4` and `y = 1` as a solution. `3ax-7y=5`.
View SolutionFind the solutions of form `x = a, y = 0` and `x= 0, y= b` for the following pairs of equations. Do they have any common such solution ? `7x+3y=42` and `2x+5y=12`.
View SolutionFind the solutions of form `x = a, y = 0` and `x= 0, y= b` for the following pairs of equations. Do they have any common such solution ? `2x+9y=18` and `3x-4y=24`.
View SolutionIf the point (3, 4) lies on the graph of the equation `3y = ax + 7`, Find the value of `a`.
View SolutionThe taxi fare in a city is as follows : For the first kilometre, the fare is Rs.8 and for the subsequent distance it is Rs.5 per kilometre. Taking the distance covered as x km and total fare as Rs.y, write a linear equation for this information and draw its graph.
View SolutionDraw the graph of `x + 2y = 6`.
View SolutionDraw the graph of `x + y = 1`.
View SolutionAs you know that acceleration produced in a body is directly proportional to the applied force. Express the given situation in the form of a equation and draw the graph of the equation.
View SolutionChoose the correct equation from the choices given for the following graph :
 .
.
View SolutionChoose the correct equation from the choices given for the following graph :
 .
.
View SolutionChoose the correct equation from the choices given for the following graph :
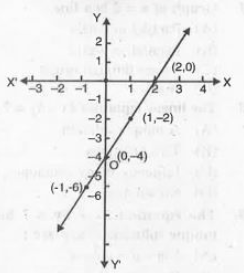 .
.
View SolutionGive the geometric representation of y = 3 as an equation in one variable.
View SolutionGive the geometric representation of y = 3 as an equation in two variables.
View SolutionGive the geometric representation of `2x + 9 = 0` as an equation in one variable.
View SolutionGive the geometric representation of `2x + 9 = 0` as an equation in two variable.
View SolutionExpress `Y = -4` graphically in terms of one variable.
View SolutionExpress `Y = -4` graphically in terms of one variable.
View SolutionSolve `2x + 1 = x - 3` and express it graphically in terms of one variable.
View SolutionSolve `2x + 1 = x - 3` and express it graphically in terms of two variable.
View SolutionThe solution of the equation `x - 2y = 4` is :
View SolutionIn graphical representation of `y = - 4`, line is :
View SolutionSolution of equation `2x + 1 = x + 3` is :
View SolutionThe graph of line `x - y = 0` passes through :
View SolutionThe graph of line `x + y =7` intersect the x-axis at :
View SolutionPoint `(4, 1)` lies on the line :
View SolutionGraph of `x = 2` is a line :
View SolutionThe linear equation `2x - 5y = 7` has
View SolutionThe equation `2x + 5y = 7` has a unique solution, if x, y are :
View SolutionIf (2, 0) is a solution of the linear equation 2x + 3y = k, then the value of k is
View SolutionAny solution of the linear equation `2x + 0y + 9 = 0` in two variables is of the form
View SolutionThe graph of the linear equation 2x + 3y = 6 cuts the y-axis at the point
View SolutionThe equation x = 7, in two variables, can be written as
View SolutionAny point on the x-axis is of the form
View SolutionAny point on the line y = x is of the form
View SolutionThe equation of x-axis is of the form
View SolutionThe graph of y = 6 is a line
View Solution`x = 5,y = 2` is a solutioin of the linear equatioin
View SolutionIf a linear equation has solutions `(- 2, 2), (0, 0)` and `(2,- 2)`, then it is of the form
View SolutionThe positive solutions of the equation is `ax+by+c=0` always lie in the
View SolutionThe graph of the linear equation `2x + 3y = 6` is a line which meets the x-axis at the point
View SolutionThe graph of the linear equation y = x passes through the point
View SolutionIf we multiply or divide both sides of a linear equation with a non-zero number, then the solution of the linear equation :
View SolutionHow many linear equationsin x and y can be satisfied by x = 1 and y = 2 ?
View SolutionThe point of the form (a, a) always lies on :
View SolutionThe point of form `(a, -a)` always lies on the line
View SolutionWrite whether the following statement is True or False ? Justify your answers : The point (0, 3) lies on the graph of the linear equation `3x + 4y = 12`.
View SolutionWrite whether the following statement is True or False ? Justify your answers : The graph of the linear equation `x+2y=7` passes through the point (0, 7).
View SolutionWrite whether the following statement is True or False ? Justify your answers : The graph represents the linear equation x + y = 0.
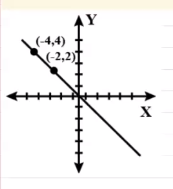
View SolutionWrite whether the following statement is True or False ? Justify your answers : Every point on the graph of a linear equation in two variables does not represent a solution of the linear equation.
View SolutionWrite whether the following statement is True or False ? Justify your answers : The graph of every linear equation in two variables need not be a line.
View Solution
Exercise questions and complete solutions for chapter Linear Equations In Two Variables of MBD of Class 9