Complete Solutions to Exercise of chapter Introduction To Euclid's Geometry of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | Introduction To Euclid's Geometry |
| MBD | Exercise |
| Number Of Questions | 52 |
| Academic Year | 2023-24 |
The following statement is true or false ? Give reasons for your answer : Only one line can pass through a single point.
View SolutionThe following statement is true or false ? Give reasons for your answer : There are infinite number of lines which pass through two distinct points.
View SolutionThe following statement is true or false ? Give reasons for your answer : A terminated line can be produced indefinitely on both the sides.
View SolutionThe following statement is true or false ? Give reasons for your answer : If two circles are equal, then their radii are equal.
View SolutionThe following statement is true or false ? Give reasons for your answer : In fig
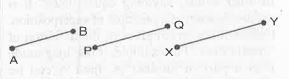 if AB = PQ and PQ = XY, then AB = XY.
if AB = PQ and PQ = XY, then AB = XY.
View SolutionGive a definition for the following term. Is there other term that need to be defined first ? What is it and how might you define it ? Parallel Lines.
View SolutionGive a definition for the following term. Is there other term that need to be defined first ? What is it and how might you define it ? Perpendicular Lines.
View SolutionGive a definition for the following term. Is there other term that need to be defined first ? What is it and how might you define it ? Lines Segment.
View SolutionGive a definition for the following term. Is there other term that need to be defined first ? What is it and how might you define it ? Radius of a Circle.
View SolutionGive a definition for the following term. Is there other term that need to be defined first ? What is it and how might you define it ? Square.
View SolutionConsider ‘postulate’ given below. Given any two distinct points A and B, there exists a third point C which is between A and B. Do this postulate contains any undefined term ? Is this postulate consistent ? Do they follow from Euclid’s postulate ? Explain.
View SolutionConsider ‘postulate’ given below. There exist at least three points that are not on the same line. Do this postulate contains any undefined term ? Is this postulate consistent ? Do they follow from Euclid’s postulate ? Explain.
View SolutionIf a point C lies between two points A and B such that AC = BC, then prove that `AC=1/2AB`. Explain by drawing the figure.
View SolutionA point C lies between two points A and B such that AC = BC, then `AC=1/2AB`. Point C is called a midpoint of line segment AB. Prove that every line segment has one and only one midpoint.
View SolutionIn Fig.
 if AC = BD, then prove that AB = CD.
if AC = BD, then prove that AB = CD.
View SolutionWhy is axiom 5, in the list of Euclid’s axioms, considered as a ‘universal truth’ ?
View SolutionUsing Euclid’s axioms/postulates bisect a given finite straight line.
View SolutionUsing Euclid’s axiom or postulate, prove the proposition that if in a triangle two angles are equal to one another, then the opposite sides are equal.
View SolutionUsing Euclid’s axiom or postulate, prove the proposition that if in a triangle two angles are equal to one another, then the opposite sides are equal.
View SolutionHow would you rewrite Euclid’s fifth postulate so that it would be easier to understand ?
View SolutionDoes Euclid’sfifth postulate imply the existence of parallel lines ? Explain.
View SolutionThe three steps from solids to points are :
View SolutionThe number of dimensions, a solid has :
View SolutionThe number of dimensions, a surface has :
View SolutionThe number of dimensions, a point has :
View SolutionEuclid divided his famous treatise “The Elements” into :
View SolutionThe total number of propositions in the Elements are :
View SolutionBoundaries of solids are :
View SolutionBoundaries of surfaces are :
View SolutionIn Indus Valley Civilisation (about 300 B.C.), the bricks used for construction work were having dimensions in the ratio :
View SolutionA pyramid is solid figure, the base of which is :
View SolutionThe side faces of a pyramid are :
View SolutionIt is known that if x + y = 10 then x + y + z = 10 + z. The Euclid’s axiom that illustrates this statement is :
View SolutionIn ancient India, the shapes of altrars used for house hold rituals were :
View SolutionThe number of interwoven isosceles triangles in Sriyantra (in the Atharvaveda) is :
View SolutionGreek’s emphasised on :
View SolutionIn Ancient India, Altars with combination of shapes like rectangles, triangles and trapeziums were used for :
View SolutionEuclid belongs to the country :
View SolutionThales belongs to the country :
View SolutionPythagoras was a student of :
View SolutionWhich of the following needs a proof ?
View SolutionEuclid stated that all right angles are equal to each other in the form of :
View SolutionLines are parallel if they do not intersect is stated in the form of :
View SolutionEuclidean geometry is valid only for curved surfaces.
View SolutionThe boundaries of the solids are curves.
View SolutionWrite True or False and Justify Your answer The edges of a surface are curves.
View SolutionThe things which are double of the same thing are equal to one another.
View SolutionIf a quantity B is a part of another quantity A, then A can be written as the sum of B and some third quantity C.
View SolutionThe statements that are proved are called axioms.
View Solution‘‘For every line `l` and for every point P not lying on a given line `l`, there exists a unique line `m` passing through P and parallel to `l`” is known as Playfair’s axiom.
View SolutionTwo distinct intersecting lines cannot be parallel to the same line.
View SolutionAttempts to prove Euclid’s fifth postulate using the other postulates and axioms led to the discovery of several other geometries.
View Solution
Exercise questions and complete solutions for chapter Introduction To Euclid's Geometry of MBD of Class 9