Complete Solutions to EXERCISE of chapter SURFACE AREAS AND VOLUMES of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | SURFACE AREAS AND VOLUMES |
| MODERN PUBLICATION | EXERCISE |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
Find the lateral surface and total surface area of a cuboid of length 80 cm, breadth 40 cm and height 20 cm.
View SolutionFind the total lateral surface area of a cube of edge is 10 cm.
View SolutionThe latera surface area of a cube is 1014 sq.cm, find the main diagonal of the cube.
View SolutionThe lateral surface area of a cube is `64 m^2` find its total surface area.
View SolutionFind the ratio of the total surface area and lateral surface area of a cube.
View SolutionThe dimensions of a room are `5mxx4mxx3m`. Find the cost of white washing the walls of the room and the ceiling at the rate of `Rs 11.5 per m^2`.
View SolutionFind the length of the longest rod that can be placed in a room 12 m long 9 m broad and 8 m high.
View SolutionCan we construct a cube whose length of main diagonal is `13sqrt3cm` and diagonal of the face is `12sqrt2`cm?
View SolutionThree equal cubes are placed adjacently in a row. Find the ratio of total surface of the new cuboid to that of the sum of their surface areas of the three cubes.
View SolutionThe momentum of a body is increased by 50% what is the percentage increase in its K. E.?
View SolutionThe cost of preparing the walls of a room 12 m long at the rate of Rs 1.35 per square metre is Rs 340.20 and the cost of matting the floor at 85 paise per square metre is Rs 91.80 find the height of the room.
View SolutionThe length and breadth of a room are in the ratio 4:3 and its height is 5.5 meters. The cost of decorating its wall including doors and windows at Rs 6.60 per square metre is Rs 5082. find the length and breadth of the room.
View SolutionA class room is 7 m long, 6.5 m wide and 4 m high. It has one door 3 m x 1.5 m and three windows, each measuring 2 m x 1 m. The interiror walls are to be colour washed. The contractor charges Rs 5.25 per sq. m. Find the cost of colour washing.
View SolutionIf V is the volume of a cuboid of dimensions a,b,c and S is its surface area, then prove that
`1/V=2/S(1/a+1/b+1/c)`
View SolutionThe areas of three adjacent faces of a cuboid are x,y and z. if the volume is V, prove that `V^2=xyz`.
View SolutionFind the volume of the cuboid whose dimensions are
length=26m, breadth=14m and height=6.5m
View SolutionFind the volume of the cuboid whose dimensions are
length=24 m, breadth=25 m and height =6m.
View SolutionIf the areas of three adjacent faces of a cuboid are `8cm^2,18cm^2` and `25cm^2`. Find the volume of the cubiod.
View SolutionThe breadth of a room is twice its height and is half of its length. The volume of room is `512 dm^3`. Its dimensions are :
View SolutionTwo cubes, each of volume `512cm^3` are joined end to end. Find the surface area of the resulting cuboid.
View SolutionHow many planks of dimensions `(5mxx25cmxx10cm)` can be stored in a pit which is 20 m long, 6m wide and 80 cm deep?
View SolutionHow many bricks will be required to construct a wall 12 m three smaller cubes. If the edges of the two smaller cubes are 6 cm and 8 cm, find the edge of the third smaller cube.
View SolutionGiven that 1 cubic cm of marble weights 0.25 kg, the weight of marble block 28 cm in width and 5 cm thick is 112kg. Find the length of the block.
View SolutionA river 3 m deep and 40 m wide is flowing at the rate of 2 km per hour. How much water will fall into the sea in a minute?
View SolutionHow many persons can be accommondatd in a dining hall of dimensions `(20cmxx16cmxx4.5cm)`, assuming that each persons requires 5 cubic metres of air?
View SolutionThe volumes of a cuboid is `1536cm^2`. Its length is 16 m and its breadth and height are in the ratio 3:2. find the breadth and height of the cuboid.
View SolutionIn a shower, 5 cm of rain falls, find the volume of water that falls on 2 hectares of graound.
View SolutionA rectangular container, whose base is a square of side 5 cm, stands on a horizontal table, and holds water up to 1 cm from the top. When a cube is placed in the water it is completely submerged, the water rises to the top and 2 cubic cm of water overflows. Calculate the volume of the cube and also the length of its edge.
View SolutionA field is in the form of a rectangle of length 18 m and width 15 m. A pit, 7.5 m long, 6 m broad and 0.8 m deep, is dug in a corner of the field and the earth taken out is spread over the remaining area of the field. Find out the extent to which the level of the field has been raised.
View SolutionA rectangular tank is 80 m long and 25 m braod water flows into it through a pipe whose cross section is `25 cm^2`, at the rate of 16 km per hour. How much the level of the water rises in the tank in 45 minutes.
View SolutionFind the curved surface area of a right circular cylinder at height 21 cm and base radius 5 cm.
View SolutionThe diameter of a cylinder is 28 cm and its height is 40 cm. find the curved surface area and the total surface area of the cylinder.
View SolutionA solid cylinder has total surface area of `462 cm^2`. Its curved surface area of one third of its total surface area. Find the radius and height of the cylinder.
View SolutionFind the ratio between the total surface area of a cylinder to its curved surface area, given that its height and radius are 7.5 cm and 3.5 cm respectively.
View SolutionThe total surface area of a hollow metal cylinder, open at both ends, of external radius 8cm and height 10cm is `338picm^2`.Taking r cm to be inner radius, write down an equation in r and use it to find the thickness of the metal in the cylinder.
View SolutionThe diameter of a roller 1.5 m long is 84 cm. If it takes 100 revolutions to level a playground, find the cost of levelling this ground at the rate of 50 paise per square meter.
View SolutionA cylindrical vessel, without lid, has to be tin-coated on its both sides. If the radius of the base is 70cm and its height is 1.4m, calculate the cost of tin-coating at the rate of Rs. 3.50 per `1000 cm^2`.
View Solution50 circular plates each of radius 7 cm and 1 thickness `1/2` cm are placed one above another to form a solid right circular cylinder. Find the total surface area and volume of the cylinder so formed.
View SolutionThe area of the curved surface of a cylinder is 4400 sq.cm and the circumference of its base is 110 cm. find the height of the cylinder.
View SolutionForty cylindrical pillars of the building are to be cleaned. If the diameter of the pillar is 0.50 m and height is 4 m. find the cost of cleaning them at the rate of Rs `2.50 per m^2`.
View SolutionFind the cost of sinking tube well 280 m deep having diameter 3 m at the rate of Rs `3.60 per m^2`?
View SolutionThe diameter of a cylindrical well is 4.5 m and depth of the well is 14m. Find the cost of cementing its inner curved surface at the rate of Rs 12.50 per sq. metre.
View SolutionFind the volume of a right circular cylinder of height 21 cm and base radius 5 cm.
View SolutionThe diameter of a cylinder is 28 cm and its height is 40 cm. find the volume of the cylinder.
View SolutionThe area of the curved surface of a cylinder is 4400 sq.cm and the circumference of its base is 110 cm. find the height of the cylinder.
View SolutionThe sum of the radius of the base and the height of a solid cylinder is 37 cm. If the total surface area of the solid cylinder is 1628 `cm^2`, find the volume of the cylinder.
View SolutionThe ratio between curved surface area and total surface area of right circular cylinder is `1:2` find the ratio between the height and the radius of the cylinder.
View SolutionThe radii of two cylinders are in the ratio 2:3 and their heights are in the ratio 5:3. Calculate the ratio of their volumes and the ratio of their curved surfaces.
View SolutionThe ratio between the radius of the base and the height of cylindrical is 2:3. Find the total surface area of the cylinder, if its volume is `1617 cm^3`
View SolutionThe curved surface area of a cylindrical pillar is `264 m^2` and its volume is `924 m^3`. Find the diameter and the height of the pillar.
View SolutionFind the weight of a lead pipe 3.5 m long. The external diameter of pipe is 2.4 cm and thickness of the pipe is 3 mm and 1 cm. of lead weights 10 g.
View SolutionHow many cubic metres of earth must be dug out to sink a well 14 m deep and 4 m in diameter? What will it cost to plaster its inner surface at Rs 2.50 per square metre?
View SolutionA powder tin has a square base with side 12 cm and height 17.5 cm. another is cylindrical with diameter of its base 12 cm and height 17.5 cm. which has more more capacity and by how much?
View SolutionA copper rod of diameter 1 cm and length 8 cm is drawn into a wire of length 18 m of uniform thickness. Find the thickness of the wire.
View SolutionThe trunk of a tree is cylindrical and its circumference is 176 cm. If the length of the trunk is 3 m, find the volume of the timber that can be obtained form the trunk.
View SolutionWater flows out through a circular pipe whose internal diameter is 2 cm, at the rate of 6 metres per second into a cylindrical tank. The water is collected in a cylindrical vessel, radius of whose base is 60 cm. find the rise in the level of water in 30 minutes?
View SolutionFrom a top of inner radius 0.75 cm, water flows at the rate of 7 m per second. Find the volume in litres of water delivered by the pipe in one hours.
View SolutionA well of diameter 2 m is dug 14 m deep. The earth taken out of it is spread evenly all around it to a width of 5 m do form an embankment. Find the height of the embankment.
View SolutionA rectangular sheet of paper `30cmx×18cm` can be transformed into the curved surface of a right circular cylinder in two ways namely, either by rolling the paper along its length or by rolling it along its breadth. Find the ratio of the volumes of the two cylinders, thus formed.
View SolutionThe barrel of a fountain-pen, cylindrical in shape, is 7 cm long and 5 mm in diameter. A full barrel of ink in the pen will be used up on writing 330 words on an average. How many words would use up a bottle of ink containing one fifth of a litre ?
View SolutionWater is flowing at the rate of 3km/h through a circular pipe of 20 cm internal diameter into a circular pipe of into a circular cisten of diameter 10m and depth 2 m. in how much time, will the cistern be filled?
View SolutionA cylindrical water tank of diameter 1.4 m and height 2.1 m is being fed by a pipe of diameter 3.5 cm through which water flows at the rate of 2 metre per second. In how many time the tank will be filled?
View SolutionFind the curved area of a cone, if its slant height is 60 cm and the radius of its base is 21 cm.
View SolutionThe radius of a cone is 7 cm and area of curved surface is `176cm^2`. Find the slant height.
View SolutionThe radius of a cone is 5 cm and vertical height is 12 cm. find the area of a curved surface.
View Solutionfind the total surface area of a right circular cone with radius 6 cm and height 8 cm.
View SolutionThe height of a cone is 21 cm. find the area of the base if the slant height is 28 cm.
View SolutionThe radius of the slant height of a cone are in the ratio of 4:7. if its curved surface area is `792 cm^2`. Find its radius.
View SolutionThe area of the curved surface of a cone is `60 picm^2`. If the slant height of the cone be 8 cm, find the radius of the base.
View SolutionThe diameter of two cones are equal. If their slant height s are in the ratio 5:4. find the ratio of their curved surface areas.
View SolutionThere are two cones, the curved surface area of one is twice that of the other. The slant height of the later is twice that of the former. Find the ratio of their radii.
View SolutionA tent of heihgt 33 m is in the form of a right circular cylinder of diameter 120 m and height 22 m surmounted by a right circular cone of the same diameter. Find the cost of canvas of the tent at the rate of `Rs 1.50 per m^2`.
View SolutionA cylinder and a cone have equal radii of their bases and equal heights. If their curved surface areas are in the ratio 8:5, show that the radius of each is to be heihgt of each as 3:4
View SolutionThe curved surface area of a cone exceeds the base area by `88cm^2` it slant height exceeds the base radius by 4 cm. find the radius of the base.
View SolutionA tent is in the form of a right circular cylinder, surmounted by a cone. The diameter of the cylinder is 24 m. The height of the cylindrical portion is 11 m, while the vertex of the cone is 16 m above the ground. Find the area of the canvas required for the tent.
View SolutionA circus tent is cylindrical upto a height of 3 m and conical above it. If the diameter of the base is 105 m and the slant height of the conical part is 53 m, find the total cost of the canvas used to make the tent when the cost per square metre of the canvas is ? 10.
View SolutionA metallic toy is in the shape of a cylinder whose both ends are conical in shape diameter of circular cross-section of cylinder is 6 cm and its height is 10 cm the length of the toy is 18 cm find the cost of gold plating it `Rs. 100 per cm^2`.
View SolutionFind the volume of a right circular cone with
Radius 4 m and height 9 m.
View SolutionFind the volume of a right circular cone with
Diameter 5 m and height 5 m
View SolutionThe height of a right circular cone is 12 cm. if its volume is `100picm^3`, find its radius.
View SolutionVertical height of a right circular cone is four times its radius and its volume is `36picm^3`. Find the height.
View SolutionFind the volume of a cone having radius of the base 35 cm and slant height 37 cm.
View SolutionTwo cones have their heights in the ratio 1:3 and the radii of their bases in the ratio 3:1. show that their volumes are in the ratio 3:1.
View SolutionThe ratio of volumes of two cones is 4:5 and the ratio of the radii of their bases is 2:3. find the ratio of their vertical heights.
View SolutionThe radius and the height of a right circular cone are in the ratio 5 : 12. If its volume is `314 cm^3`, find the slant height and the radius of the cone. [Use `pi` = 3.14]
View SolutionIf the radius of the base of a cone is halved, keeping the height same, what is the ratio of the volume of the reduced cone to that of the original cone?
View SolutionFind the weight of a solid cone whose base is of diameter 14 cm and vertical height 51 cm, supporting the material of which it is made weighs 10 grams per cubic cm.
View SolutionA right angled triangle of which the sides containing the right angle are 6.3cm and 10cm in length, is made to turn around on the longer side. Find the volume of the solid thus generated.
View SolutionA tent is in the form of right circular cone of height 6m , the diameter of base 7m . If 12 adults can sleep in it , find the average cubic metre of air space required per adult.
View SolutionA right circular cone is 3.6 cm high and the radius of its base is 1.6 cm. it is melted and recast into a right circular cone with radius of its base as 1.2 cm. find its height.
View SolutionA conical vessel whose internal radius is 5 cm and height of 24 cm is full of water. The water is emptied into a cylindrical vessel with internal radius 10 cm. Find the height to which the liquid rises.
View SolutionAn iron pillar consists of a cylindricla portion 2.8 m high and 20 m in diamter and a cone 42 cm. high is surmounting it. Find the weight of the pillar, given that `1cm^3` of iron weights 7.5 g.
View SolutionFrom a solid right circular cylinder with height 10 cm and radius of the base 6 cm, a right circular cone of the same height and base if removed. Find the volume of the remaining solid.
View SolutionWater flows a the rate of 10 metres per minute through a cylindrical pipe 5 mm in diameter. How long would it take to fill a conical vessel whose diameter at the surface is 40 cm and depth `24cm^2`.
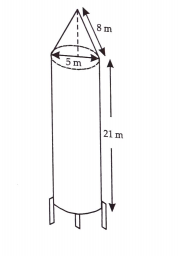
View SolutionA rocket is in the form of a circular cylinder closed at the lower end with a cone of the same radius attached to the top. The cylinder is of radius 2.5m and height 21m and the cone has the slant height 8m. Calculate the total surface area and the volume of the rocket.
View SolutionFind the surface area of the sphere of radius:
10.5 cm
View SolutionFind the surface area of the sphere of radius:
5 cm?
View SolutionFind the surface area of a sphere of diameter
14 cm?
View SolutionAssume ` pi = (22)/( 7)` , unless stated otherwise .
Find the surface area of a sphere of diameter :
21 cm
View SolutionFind the curved surface area and total surface area of hemisphere of radius 14 cm.
View Solution
EXERCISE questions and complete solutions for chapter SURFACE AREAS AND VOLUMES of MODERN PUBLICATION of Class 9