Complete Solutions to Exercise 8b of chapter QUADRILATERALS of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | QUADRILATERALS |
| NAGEEN PRAKASHAN | Exercise 8b |
| Number Of Questions | 15 |
| Academic Year | 2023-24 |
The sides AB and AC are equal of an isosceles triangle ABC. D E and F are the mid-points of sides BC, CA and AB respectively. Prove that:
(i) Line segment AD is perpedicular to line segment EF.
(ii) Line segment AD bisects the line segment EF.
View SolutionShow that the quadrialteral formed by joining the mid-points of the consecutive sides of a rhombus, is a rectangle.
View SolutionE is the mid-point of the median AD of `DeltaABC.` Line segment BE meets AC at point F when produce, prove that `AF=1/3AC.`
View SolutionShow that the quadrilateral, formed by joining the mid-points of the sides of a square is also a square.
View SolutionShow that, in a parallelogram ABCD, the internal and external bisectors of `angleA and angleB` from a rectangle.
View SolutionProve that the quadrilateral formed by joining the mid-points of the pairs of consecutive sides of a quadrilateral is a parallelogram.
View SolutionIn `DeltaABC,angleB=90^(@).` If P is the mid-point of side AC, then
`PA=PB=`
View Solution`squarePQRS` is a reactangle. If A, B and C are the mid-points of PQ, PS and QR respectively, then prove that
`AB+AC=1/2(PR+SQ).`
View Solution`P ,Q` and `R` are, respectively, the mid-points of sides `B C ,C A` and `A B` of a triangle `A B C` , `P R` and `B Q` meet at `XdotC R` and `P Q` meet at `Y` . Prove that `X Y=1/4B Cdot`
View SolutionIn `DeltaPQR,Pq=PR` and S is the mid-point of PQ. A line drawn from S parallel to QR, intersects the line PR at T. Prove that PS = PT.
View SolutionThe points M and N divide the line seqment AB of `DeltaABC` in three equal parts. If `MP"||"NQ"||"BC` and points P and Q lie on line AC, then prove that P and Q trisect the line AC.
View SolutionIn the adjoining figure, two points A and B lie on the same side of a line 'l'. C is the mid-point of AB. If AD `botlandBEbotl,` then prove that CD = CE.
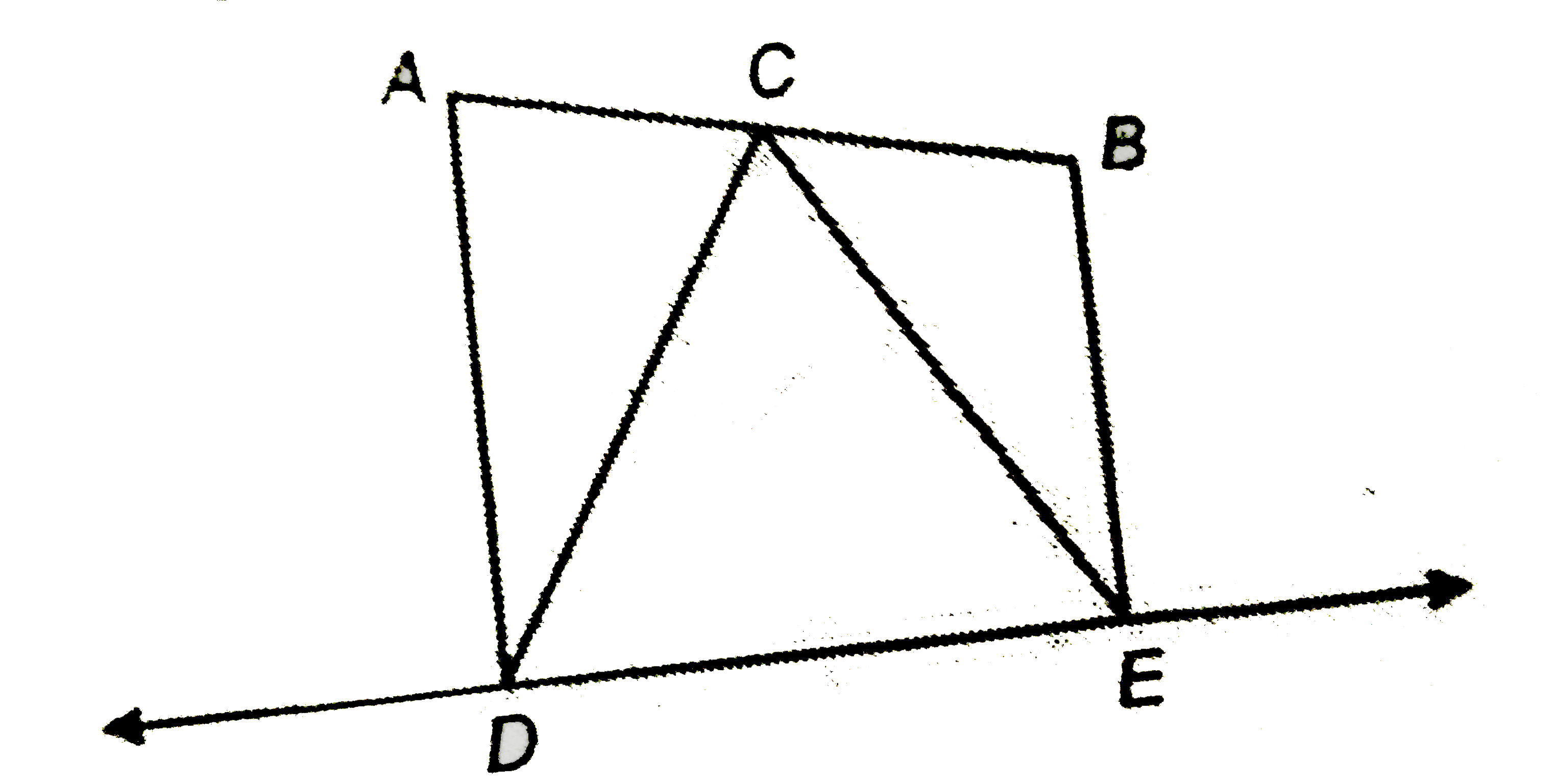
View SolutionAB and CD are the parallel sides of a trapeziuml. E is the mid-point of AD. A line through E and parallel to side AB meets the line BC at point F. Prove that F is the mid-point of BC.
View SolutionProve that a line drawn from the vertex of a triangle to its base is bisected by the line joining the mid points of the remaining two sides of the triangle.
View SolutionIn a parallelogram ABCD, E and F are the mid-points of sides BC and AD respectively. Show that the line segment BF and ED trisect the diagonal AC.
View Solution
Exercise 8b questions and complete solutions for chapter QUADRILATERALS of NAGEEN MATHS (HINGLISH) of Class 9