Complete Solutions to EXERCISE - 15.3 of chapter PROOFS IN MATHEMATICS of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | PROOFS IN MATHEMATICS |
| NCERT BANGLISH | EXERCISE - 15.3 |
| Number Of Questions | 6 |
| Academic Year | 2023-24 |
Take any three consecutive odd numbers and find their product,
for example `1 xx 3 xx 5 = 15 , 3 xx 5 xx 7 = 105 , 5 xx 7 xx 9 -.......... ` Is there any pattern you can guess in these products? What can you conjecture about them?
View SolutionTake any three consecutive even numbers and add them , say ,
` 2+4 + 6= 12 , 4 +6 + 8 = 18 , 6 + 8 + 10 = 24 , 8 + 10 + 12 = 30` and so on.
Is there any pattern can you guess in these sums? What can you conjecture about them?
View SolutionGo back to Pascal's triangle .
Line -1 : ` 1=11^(0)`
Line -2 : ` 11 = 11^(1)`
Line-3 : `121 = 11^(2)`
Make a conjecture about Line-4 and Line-5 .
Does your conjecture hold ? Does your conjecture hold for Line -6 too ?
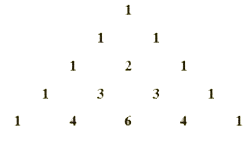
View SolutionLook at the following pattern :
(i) `28 = 2^(2) xx 7^1` , Total number of factors (2+1) (1+1)=` 3 xx 2 =6`
28 is divisible by 6 factors i.e., 1,2,4,7,14,28
(ii) ` 30=2^(1) xx 3^(1) xx 5^(1)` , Total number of factors `( 1+1)(1+1)(1+1)=2 xx 2 xx 2 =8`
30 is divisible by 8 factor i.e., 1,2,3,5,6,10,15,30 find pattern
View SolutionLook at the following pattern:
`1^(2) = 1`
`11^(2) =121`
`111^2 = 12321`
`1111^(2)=1234321`
`11111^2 = 123454321`
Make a conjecture about about each of the following :
` 111111^2=..............`
` 1111111^2=...........`
Check if your conjecture is true .
View SolutionIn a polynomial `p(x)=x^(2) + x + 41` put different value of x and find p (x). Can you conclude after putting different value of x that p(x) is prime for all. Is x an element of N ? Put x=41 in p(x). Now what do you find ?
View Solution
EXERCISE - 15.3 questions and complete solutions for chapter PROOFS IN MATHEMATICS of NCERT MATHEMATICS(BENGALI ENGLISH) of Class 9