Complete Solutions to प्रश्नावली 7.4 of chapter त्रिभुज of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | त्रिभुज |
| NCERT EXEMPLAR HINDI | प्रश्नावली 7.4 |
| Number Of Questions | 21 |
| Academic Year | 2023-24 |
एक समबाहु त्रिभुज के सभी कोण ज्ञात कीजिए।
View Solutionसिद्ध कीजिए कि दर्पण में प्रतिबिम्ब दर्पण के पीछे उतनी ही दूरी पर बनता है जितनी दूरी बिम्ब दर्पण के सामने है।
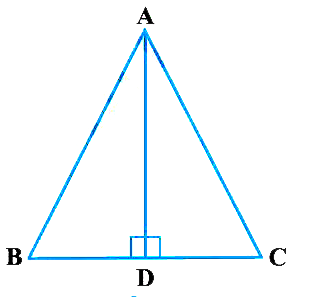
View SolutionAB = AC वाला ABC एक समद्विबाहु त्रिभुज है तथा D भुजा BC पर इस प्रकार स्थित है कि `AD _|_ BC` है। `angle BAD = angle CAD` सिद्ध करने के लिए, किसी विद्यार्थी ने निम्नलिखित प्रक्रिया अपनाई :
`Delta ABD` और `Delta ACD` में,
AB = AC (दिया है)
`angle B = angle C` (क्योंकि AB = AC)
तथा `angle ADB = angle ADC` (प्रत्येक `90^(@)`)
अतः, `Delta ABD ~= Delta ACD " " (A AS)`
सलिए, `angle BAD = angle CAD " " (CPCT)`
उपरोक्त तर्कणों में क्या कमी है ?
View Solutionकोण `angleABC`के समद्विभाजक पर स्थित एक बिन्दु P है | यदि P से AB से के समान्तर एक रेखा BC को Q पर काटती है, तो सिध्द करो कि PBQ त्रिभुज समद्विबाहु है |
View SolutionABCD एक चतुर्भुज है, जिसमें AB = CD और AD = BC । दर्शाइए कि BD दोनों कोणों ABC और ADC को समद्विभाजित करता है।
View SolutionABC एक समकोण त्रिभुज है, जिसमें AB = AC है। `angle A` का समद्विभाजक BC से D पर मिलता है। सिद्ध कीजिए कि BC = 2 AD है।
View SolutionO एक वर्ग ABCD के अभ्यंतर में स्थित बिंदु इस प्रकार है कि OAB एक समबाहु त्रिभुज है। सिद्ध कीजिए कि `Delta OCD` एक समद्विबाहु त्रिभुज है।
View Solutionएक ही आधार BC पर दो त्रिभुज ABC तथा DBC इस प्रकार स्थित है कि बिंदु A तथा D रेखा BC के विपरीत दिशाओं में है। यदि `ar(DeltaABC)=ar(DeltaDBC)` हो, तो दर्शाइए कि BC रेखा AD को समद्विभाजित करती है।
View SolutionABC एक समद्विबाहु त्रिभुज है, जिसमें AC = BC है। AD और BE क्रमशः BC और AC पर शीर्षलंब है। सिद्ध कीजिए कि AE = BD है।
View Solutionसिद्ध कीजिए कि एक त्रिभुज में किन्ही दो भुजाओं का योग तीसरी भुजा की माध्यिका के दो गुने से बड़ा होता है।
View Solutionदर्शाइए कि एक चतुर्भुज ABCD में, `AB+BC+CD+DA lt 2(BD+AC)` होता है।
View Solutionदर्शाइए कि एक चतुर्भुज ABCD में, `AB+BC+CD+DA gt AC+BD` होता है।
View Solutionएक त्रिभुज ABC में, D भुजा AC का मध्य - बिंदु है ताकि `BD=(1)/(2)AC` है। दर्शाइए कि `angle ABC` एक समकोण है।
View Solutionसिध्द करो की एक समकोण त्रिभुज के कर्ण के मध्यबिंदु को सम्मुख शीर्ष से मिलाने वाला रेखाखण्ड, कर्ण का आधा होता है ।
View Solutionयदि बिंदु P, परस्पर बिंदु A पर काटने वाली रेखाओं l और m से समदूरस्थ हो तो सिद्ध कीजिए कि रेखा AP रेखाओं l और m के बीच बने कोण का समद्विभाजक है।
View Solutionएक समलंब ABCD की क्रमशः समांतर भुजाओं AB और DC के मध्य - बिंदुओं M और N को मिलाने वाला रेखाखंड दोनों भुजाओं AB और DC पर लंब है। सिद्ध कीजिए कि AD = BC है।
View SolutionABCD एक चतुर्भुज इस प्रकार है कि विकर्ण AC दोनों कोणों A और C का समद्विभाजक है। सिद्ध कीजिए कि AB = AD और CB = CD है।
View SolutionABC एक समकोण त्रिभुज है, जिसमें AB = AC है तथा `angle C` का समद्विभाजक भुजा AB को D पर प्रतिच्छेद करता है। सिद्ध कीजिए कि `AC+AD=BC` है।
View SolutionAB और CD क्रमशः एक चतुर्भुज ABCD की सबसे छोटी और सबसे बड़ी भुजाएँ है। `angle B` और `angle D` में से निश्चित कीजिए कि कौन बड़ा है।
View Solutionसिद्ध कीजिए कि एक समबाहु त्रिभुज को छोड़कर, किसी त्रिभुज में सबसे लंबी भुजा का सम्मुख कोण एक समकोण के `(2)/(3)` भाग से बड़ा होता है।
View SolutionABCD एक चतुर्भुज है, जिसमें AB = AD और CB = CD है। सिद्ध कीजिए कि AC, BD का लंब समद्विभाजक है।
View Solution
प्रश्नावली 7.4 questions and complete solutions for chapter त्रिभुज of NCERT EXEMPLAR HINDI of Class 9